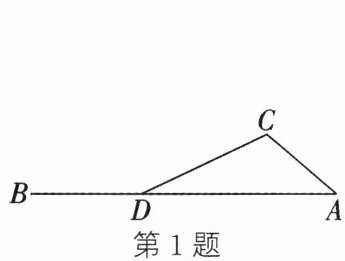
1. 如图,$\angle CDB = 155^{\circ}$,$\angle C = 115^{\circ}$,则$\angle A$的度数是(
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
C
)
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
答案:1.C
解析:
解:
∵∠CDB=155°,
∴∠CDA=180°-∠CDB=180°-155°=25°,
在△ACD中,∠C=115°,∠CDA=25°,
∴∠A=180°-∠C-∠CDA=180°-115°-25°=40°.
答案:C
∵∠CDB=155°,
∴∠CDA=180°-∠CDB=180°-155°=25°,
在△ACD中,∠C=115°,∠CDA=25°,
∴∠A=180°-∠C-∠CDA=180°-115°-25°=40°.
答案:C
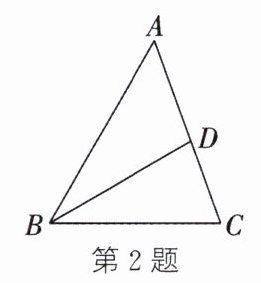
2. 如图,在$\triangle ABC$中,$\angle A = 50^{\circ}$,$\angle ABD = 30^{\circ}$,$BD$平分$\angle ABC$,则$\angle C$的度数是(
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:2.C
解析:
解:
∵BD平分∠ABC,∠ABD=30°,
∴∠ABC=2∠ABD=2×30°=60°,
∵在△ABC中,∠A=50°,
∴∠C=180°-∠A-∠ABC=180°-50°-60°=70°。
答案:C
∵BD平分∠ABC,∠ABD=30°,
∴∠ABC=2∠ABD=2×30°=60°,
∵在△ABC中,∠A=50°,
∴∠C=180°-∠A-∠ABC=180°-50°-60°=70°。
答案:C
3. 如图,$\angle A + \angle B + \angle C = 125^{\circ}$,则$\angle D + \angle E =$
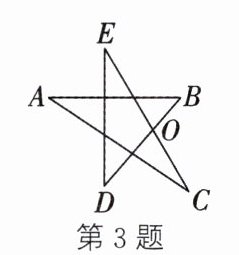
55°
.
答案:3.55°
4. 将一副三角尺按如图所示的方式摆放,其中$\angle BAC = \angle EDF = 90^{\circ}$,$\angle E = 45^{\circ}$,$\angle C = 30^{\circ}$,顶点$A$在$EF$上,顶点$D$在$BC$上,$AB$与$DF$交于点$M$.若$BC // EF$,则$\angle BMD$的度数为
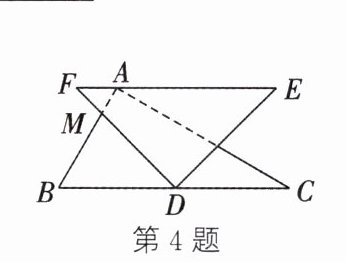
75°
.
答案:4.75°
解析:
证明:在$\triangle ABC$中,$\angle BAC=90^{\circ}$,$\angle C=30^{\circ}$,
$\therefore \angle B=180^{\circ}-\angle BAC-\angle C=60^{\circ}$。
在$\triangle DEF$中,$\angle EDF=90^{\circ}$,$\angle E=45^{\circ}$,
$\therefore \angle F=180^{\circ}-\angle EDF-\angle E=45^{\circ}$。
$\because BC// EF$,
$\therefore \angle FMB=\angle B=60^{\circ}$(两直线平行,内错角相等)。
在$\triangle FMD$中,$\angle F=45^{\circ}$,$\angle FMB=60^{\circ}$,
$\angle BMD=180^{\circ}-\angle F-\angle FMB=180^{\circ}-45^{\circ}-60^{\circ}=75^{\circ}$。
故$\angle BMD$的度数为$75^{\circ}$。
$\therefore \angle B=180^{\circ}-\angle BAC-\angle C=60^{\circ}$。
在$\triangle DEF$中,$\angle EDF=90^{\circ}$,$\angle E=45^{\circ}$,
$\therefore \angle F=180^{\circ}-\angle EDF-\angle E=45^{\circ}$。
$\because BC// EF$,
$\therefore \angle FMB=\angle B=60^{\circ}$(两直线平行,内错角相等)。
在$\triangle FMD$中,$\angle F=45^{\circ}$,$\angle FMB=60^{\circ}$,
$\angle BMD=180^{\circ}-\angle F-\angle FMB=180^{\circ}-45^{\circ}-60^{\circ}=75^{\circ}$。
故$\angle BMD$的度数为$75^{\circ}$。
5. 在$\triangle ABC$中,$\angle A = \frac{1}{2}\angle B = \frac{1}{3}\angle C$,则$\angle A$的度数为
30°
,$\angle B$的度数为60°
,这是一个直角
三角形(按角分类).答案:5.30° 60° 直角
解析:
30°;60°;直角
6. 如图,$D$是$\triangle ABC$的边$BC$上的一点,且$\angle ADC = \angle BAC$.求证:$\angle DAC = \angle B$.
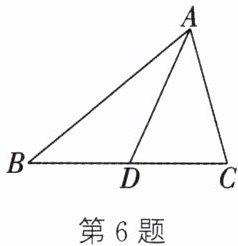

答案:6.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD.
∵∠ADC=∠BAC,
∴∠BAC=∠B+∠BAD.
∵∠BAC=∠DAC+∠BAD,
∴∠DAC=∠B
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD.
∵∠ADC=∠BAC,
∴∠BAC=∠B+∠BAD.
∵∠BAC=∠DAC+∠BAD,
∴∠DAC=∠B
7. 在$\triangle ABC$中,$\angle A = 75^{\circ}$,$\angle B - \angle C = 15^{\circ}$,则$\angle C$的度数为(
A.$30^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$10^{\circ}$
B
)A.$30^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$10^{\circ}$
答案:7.B
解析:
在$\triangle ABC$中,$\angle A + \angle B + \angle C = 180^{\circ}$,已知$\angle A = 75^{\circ}$,则$\angle B + \angle C = 180^{\circ} - 75^{\circ} = 105^{\circ}$。
又因为$\angle B - \angle C = 15^{\circ}$,联立可得:
$\begin{cases}\angle B + \angle C = 105^{\circ} \\\angle B - \angle C = 15^{\circ}\end{cases}$
两式相加得:$2\angle B = 120^{\circ}$,解得$\angle B = 60^{\circ}$。
将$\angle B = 60^{\circ}$代入$\angle B + \angle C = 105^{\circ}$,得$\angle C = 105^{\circ} - 60^{\circ} = 45^{\circ}$。
B
又因为$\angle B - \angle C = 15^{\circ}$,联立可得:
$\begin{cases}\angle B + \angle C = 105^{\circ} \\\angle B - \angle C = 15^{\circ}\end{cases}$
两式相加得:$2\angle B = 120^{\circ}$,解得$\angle B = 60^{\circ}$。
将$\angle B = 60^{\circ}$代入$\angle B + \angle C = 105^{\circ}$,得$\angle C = 105^{\circ} - 60^{\circ} = 45^{\circ}$。
B
8. 如图,点$D$在$BC$的延长线上,$DE ⊥ AB$于点$E$,交$AC$于点$F$.若$\angle A = 35^{\circ}$,$\angle D = 15^{\circ}$,则$\angle ACB$的度数为(
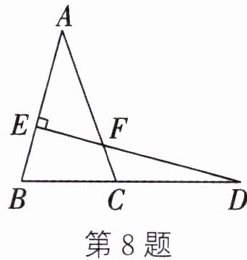
A.$65^{\circ}$
B.$70^{\circ}$
C.$75^{\circ}$
D.$85^{\circ}$
B
)
A.$65^{\circ}$
B.$70^{\circ}$
C.$75^{\circ}$
D.$85^{\circ}$
答案:8.B
解析:
证明:
∵ $DE ⊥ AB$,
∴ $\angle AEF = 90°$。
在$\triangle AEF$中,$\angle A = 35°$,
∴ $\angle AFE = 180° - \angle A - \angle AEF = 180° - 35° - 90° = 55°$。
∵ $\angle AFE = \angle CFD$(对顶角相等),
∴ $\angle CFD = 55°$。
在$\triangle CFD$中,$\angle D = 15°$,
∴ $\angle ACB = \angle CFD + \angle D = 55° + 15° = 70°$。
答案:B
∵ $DE ⊥ AB$,
∴ $\angle AEF = 90°$。
在$\triangle AEF$中,$\angle A = 35°$,
∴ $\angle AFE = 180° - \angle A - \angle AEF = 180° - 35° - 90° = 55°$。
∵ $\angle AFE = \angle CFD$(对顶角相等),
∴ $\angle CFD = 55°$。
在$\triangle CFD$中,$\angle D = 15°$,
∴ $\angle ACB = \angle CFD + \angle D = 55° + 15° = 70°$。
答案:B