1. 六边形的内角和为(
A.$180^{\circ}$
B.$360^{\circ}$
C.$540^{\circ}$
D.$720^{\circ}$
D
)A.$180^{\circ}$
B.$360^{\circ}$
C.$540^{\circ}$
D.$720^{\circ}$
答案:1.D
2. 一个多边形的内角和为$1260^{\circ}$,则这个多边形是(
A.七边形
B.八边形
C.九边形
D.十边形
C
)A.七边形
B.八边形
C.九边形
D.十边形
答案:2.C
解析:
设这个多边形的边数为$n$,根据多边形内角和公式$(n - 2) × 180^{\circ} = 1260^{\circ}$,解得$n - 2 = 7$,$n = 9$。C
3. (2024·济南)若正多边形的一个外角的度数是$45^{\circ}$,则这个正多边形是(
A.正六边形
B.正七边形
C.正八边形
D.正九边形
C
)A.正六边形
B.正七边形
C.正八边形
D.正九边形
答案:3.C
解析:
因为多边形的外角和为$360^{\circ}$,正多边形的每个外角都相等,所以这个正多边形的边数为$360^{\circ}÷45^{\circ}=8$,故这个正多边形是正八边形。
C
C
4. (2025·甘肃)如图,一张多边形纸片的内角和为$1620^{\circ}$,按图示的剪法剪去一个内角后,所得新多边形的边数为(
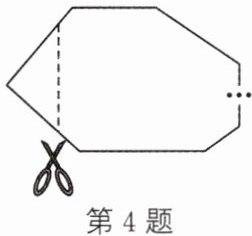
A.12
B.11
C.10
D.9
A
)
A.12
B.11
C.10
D.9
答案:4.A
解析:
设原多边形的边数为$n$,由多边形内角和公式$(n - 2)×180^{\circ}=1620^{\circ}$,解得$n = 11$。按图示剪法,剪去一个内角后边数增加$1$,新多边形边数为$11 + 1 = 12$。
A
A
5. $n$边形的内角和比$(n + 1)$边形的内角和小
180
$^{\circ}$($n$为整数,且$n\geqslant3$)。答案:5.180
6. 如图,在五边形$ABCDE$中,$\angle A = 45^{\circ}$,直线$l$分别与边$AB$,$AE$相交于点$M$,$N$,则$\angle1+\angle2=$_________$^{\circ}$。
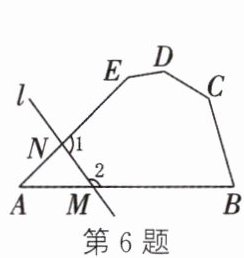

答案:6.225
解析:
解:在△AMN中,∠A=45°,
∠AMN+∠ANM=180°-∠A=135°,
∠1=180°-∠ANM,∠2=180°-∠AMN,
∠1+∠2=360°-(∠AMN+∠ANM)=360°-135°=225°。
225
∠AMN+∠ANM=180°-∠A=135°,
∠1=180°-∠ANM,∠2=180°-∠AMN,
∠1+∠2=360°-(∠AMN+∠ANM)=360°-135°=225°。
225
7. 如图,以四边形$ABCD$的各顶点为圆心,以$2$为半径画圆,则图形中各扇形(涂色部分)的面积之和是
]
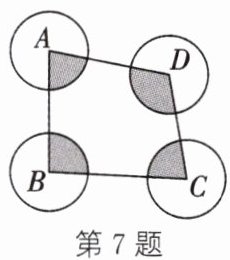
4π
。]

答案:7.4π
解析:
因为四边形内角和为$(4 - 2)×180^{\circ}=360^{\circ}$,各扇形半径均为$2$,所以各扇形面积之和为$\frac{360^{\circ}}{360^{\circ}}×\pi×2^{2}=4\pi$。
$4\pi$
$4\pi$
8. 如图,小明从点$A$出发沿直线前进$10m$到达点$B$,向左转$45^{\circ}$后又沿直线前进$10m$到达点$C$,再向左转$45^{\circ}$后沿直线前进$10m$到达点$D$……照这样走下去,小明第一次回到出发点$A$时所走的路程为
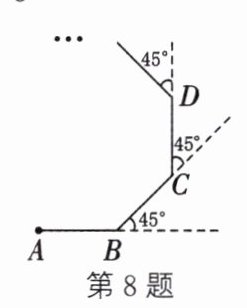
80
$m$。
答案:8.80
解析:
解:小明每次沿直线前进10m后向左转45°,可知他走过的路径是正多边形。
因为多边形外角和为360°,每次左转45°,所以边数$n = \frac{360°}{45°} = 8$。
则小明第一次回到出发点A时所走的路程为$8×10 = 80m$。
答案:80
因为多边形外角和为360°,每次左转45°,所以边数$n = \frac{360°}{45°} = 8$。
则小明第一次回到出发点A时所走的路程为$8×10 = 80m$。
答案:80
9. 如图,五边形$ABCDE$的每个内角都相等,且$AB// EC$,那么$\angle DEC$与$\angle DCE$相等吗?为什么?
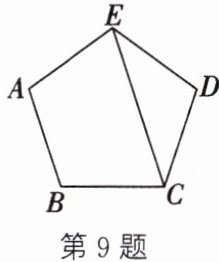

答案:9.∠DEC=∠DCE
∵ 五边形的内角和是(5-2)×180°=540°,且每个内角都相等,
∴ 每个内角的度数为540°÷5=108°,即∠A=∠AED=∠D=108°.
∵ AB//EC,
∴ ∠A+∠AEC=180°,
∴ ∠AEC=180°-∠A=72°,
∴ ∠DEC=∠AED-∠AEC=36°.
∵ △DEC的内角和为180°,
∴ ∠DCE=180°-∠DEC-∠D=36°,
∴ ∠DEC=∠DCE
∵ 五边形的内角和是(5-2)×180°=540°,且每个内角都相等,
∴ 每个内角的度数为540°÷5=108°,即∠A=∠AED=∠D=108°.
∵ AB//EC,
∴ ∠A+∠AEC=180°,
∴ ∠AEC=180°-∠A=72°,
∴ ∠DEC=∠AED-∠AEC=36°.
∵ △DEC的内角和为180°,
∴ ∠DCE=180°-∠DEC-∠D=36°,
∴ ∠DEC=∠DCE