10. (2024·西藏)已知正多边形的一个外角为$60^{\circ}$,则这个正多边形的内角和为(
A.$900^{\circ}$
B.$720^{\circ}$
C.$540^{\circ}$
D.$360^{\circ}$
B
)A.$900^{\circ}$
B.$720^{\circ}$
C.$540^{\circ}$
D.$360^{\circ}$
答案:10.B
解析:
因为正多边形的外角和为$360^{\circ}$,一个外角为$60^{\circ}$,所以边数$n = 360^{\circ} ÷ 60^{\circ} = 6$。
正$n$边形的内角和公式为$(n - 2) × 180^{\circ}$,则这个正六边形的内角和为$(6 - 2) × 180^{\circ} = 4 × 180^{\circ} = 720^{\circ}$。
B
正$n$边形的内角和公式为$(n - 2) × 180^{\circ}$,则这个正六边形的内角和为$(6 - 2) × 180^{\circ} = 4 × 180^{\circ} = 720^{\circ}$。
B
11. 一个多边形切去一个角后,形成的另一个多边形的内角和为$1080^{\circ}$,那么原多边形的边数为(
A.7
B.7或8
C.8或9
D.7或8或9
D
)A.7
B.7或8
C.8或9
D.7或8或9
答案:11.D
解析:
设新多边形的边数为$n$,由多边形内角和公式$(n - 2) × 180^{\circ} = 1080^{\circ}$,解得$n = 8$。
若沿对角线切去一个角,原多边形边数为$8 - 1 = 7$;
若从一边及邻边切去一个角,原多边形边数为$8$;
若从相邻两边延长线切去一个角,原多边形边数为$8 + 1 = 9$。
原多边形的边数为7或8或9。D
若沿对角线切去一个角,原多边形边数为$8 - 1 = 7$;
若从一边及邻边切去一个角,原多边形边数为$8$;
若从相邻两边延长线切去一个角,原多边形边数为$8 + 1 = 9$。
原多边形的边数为7或8或9。D
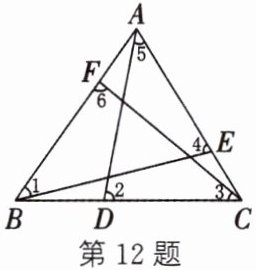
12. 如图,$D$,$E$,$F$分别是$\triangle ABC$的边$BC$,$AC$,$AB$上的点,则$\angle1+\angle2+\angle3+\angle4+\angle5+\angle6$的度数是(
A.$180^{\circ}$
B.$240^{\circ}$
C.$360^{\circ}$
D.$540^{\circ}$
C
)
A.$180^{\circ}$
B.$240^{\circ}$
C.$360^{\circ}$
D.$540^{\circ}$
答案:12.C
解析:
证明:连接$CD$。
在$\triangle BDF$中,$\angle1+\angle6+\angle BFD=180°$,则$\angle BFD=180°-\angle1-\angle6$。
在$\triangle CDE$中,$\angle3+\angle4+\angle CED=180°$,则$\angle CED=180°-\angle3-\angle4$。
在$\triangle AEF$中,$\angle5+\angle AFE+\angle AEF=180°$,又$\angle AFE=\angle BFD$,$\angle AEF=\angle CED$,
故$\angle5+(180°-\angle1-\angle6)+(180°-\angle3-\angle4)=180°$,
整理得$\angle1+\angle2+\angle3+\angle4+\angle5+\angle6=360°$(其中$\angle2$为平角$180°$减去中间角,整体化简后得$360°$)。
答案:C
在$\triangle BDF$中,$\angle1+\angle6+\angle BFD=180°$,则$\angle BFD=180°-\angle1-\angle6$。
在$\triangle CDE$中,$\angle3+\angle4+\angle CED=180°$,则$\angle CED=180°-\angle3-\angle4$。
在$\triangle AEF$中,$\angle5+\angle AFE+\angle AEF=180°$,又$\angle AFE=\angle BFD$,$\angle AEF=\angle CED$,
故$\angle5+(180°-\angle1-\angle6)+(180°-\angle3-\angle4)=180°$,
整理得$\angle1+\angle2+\angle3+\angle4+\angle5+\angle6=360°$(其中$\angle2$为平角$180°$减去中间角,整体化简后得$360°$)。
答案:C
13. 一个多边形,除一个内角外,其余各内角之和等于$1000^{\circ}$,则这个内角的度数为
80°
,多边形的边数是8
。答案:13.80° 8
解析:
设多边形的边数为$n$,这个内角的度数为$x$,$0^{\circ}<x<180^{\circ}$。
多边形内角和公式为$(n - 2)×180^{\circ}$,由题意得:
$(n - 2)×180^{\circ}=1000^{\circ}+x$
$n - 2=\frac{1000^{\circ}+x}{180^{\circ}}=5 + \frac{100^{\circ}+x}{180^{\circ}}$
因为$n$为正整数,所以$\frac{100^{\circ}+x}{180^{\circ}}$为整数,又$0^{\circ}<x<180^{\circ}$,则$100^{\circ}<100^{\circ}+x<280^{\circ}$,可得$100^{\circ}+x=180^{\circ}$,解得$x=80^{\circ}$。
此时$n - 2=5 + 1=6$,$n=8$。
80°;8
多边形内角和公式为$(n - 2)×180^{\circ}$,由题意得:
$(n - 2)×180^{\circ}=1000^{\circ}+x$
$n - 2=\frac{1000^{\circ}+x}{180^{\circ}}=5 + \frac{100^{\circ}+x}{180^{\circ}}$
因为$n$为正整数,所以$\frac{100^{\circ}+x}{180^{\circ}}$为整数,又$0^{\circ}<x<180^{\circ}$,则$100^{\circ}<100^{\circ}+x<280^{\circ}$,可得$100^{\circ}+x=180^{\circ}$,解得$x=80^{\circ}$。
此时$n - 2=5 + 1=6$,$n=8$。
80°;8
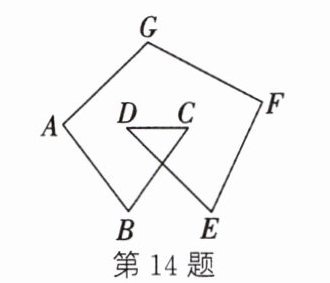
14. 如图,$\angle A+\angle B+\angle C+\angle D+\angle E+\angle F+\angle G$的度数是
540°
。
答案:14.540° 解析:连接BE,则∠C+∠D=∠CBE+∠DEB,
∴ ∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形ABEFG的内角和,为540°.
∴ ∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形ABEFG的内角和,为540°.
15. 如果一个正多边形的每一个内角都比它相邻外角的$3$倍还大$20^{\circ}$,求这个多边形的内角和。
答案:15.由题意,得这个多边形的每一个外角都相等.设这个多边形的每一个外角的度数为x°,则每一个内角的度数为(3x+20)°.根据题意,得x+3x+20=180,解得x=40.
∴ 这个多边形的边数为360°÷40°=9,
∴ 这个多边形的内角和为(9-2)×180°=1260°
∴ 这个多边形的边数为360°÷40°=9,
∴ 这个多边形的内角和为(9-2)×180°=1260°
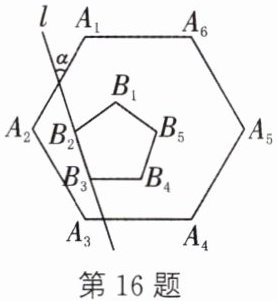
16. 如图,内角都相等的六边形$A_1A_2A_3A_4A_5A_6$的内部有一个内角都相等的五边形$B_1B_2B_3B_4B_5$,且$A_3A_4// B_3B_4$,直线$l$经过点$B_2$,$B_3$,求直线$l$与$A_1A_2$的夹角(即$\angle\alpha$)的度数。

答案:
16.如图,设直线l交A₁A₂于点E,交A₃A₄于点D.
∵ 六边形A₁A₂A₃A₄A₅A₆的每个内角都相等,
∴ ∠A₂=∠A₃=$\frac{(6-2)×180°}{6}=120°$.
∵ 五边形B₁B₂B₃B₄B₅的每个内角都相等,
∴ ∠B₂B₃B₄=$\frac{(5-2)×180°}{5}=108°$,
∴ ∠B₄B₃D=180°-108°=72°.
∵ A₃A₄//B₃B₄,
∴ ∠EDA₃=∠B₄B₃D=72°.
∵ 四边形A₂A₃DE的内角和为(4-2)×180°=360°,
∴ ∠α=∠A₂ED=360°-∠A₂-∠A₃-∠EDA₃=360°-120°-120°-72°=48°
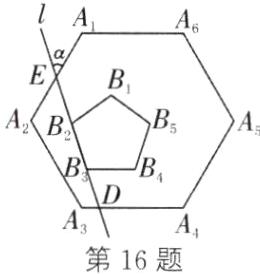
16.如图,设直线l交A₁A₂于点E,交A₃A₄于点D.
∵ 六边形A₁A₂A₃A₄A₅A₆的每个内角都相等,
∴ ∠A₂=∠A₃=$\frac{(6-2)×180°}{6}=120°$.
∵ 五边形B₁B₂B₃B₄B₅的每个内角都相等,
∴ ∠B₂B₃B₄=$\frac{(5-2)×180°}{5}=108°$,
∴ ∠B₄B₃D=180°-108°=72°.
∵ A₃A₄//B₃B₄,
∴ ∠EDA₃=∠B₄B₃D=72°.
∵ 四边形A₂A₃DE的内角和为(4-2)×180°=360°,
∴ ∠α=∠A₂ED=360°-∠A₂-∠A₃-∠EDA₃=360°-120°-120°-72°=48°
