1. 如图,由甲图案得到乙图案,可以(
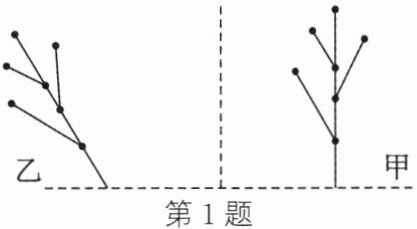
A.先旋转,后平移
B.先平移,后轴对称
C.先旋转,后轴对称
D.平移
A
)
A.先旋转,后平移
B.先平移,后轴对称
C.先旋转,后轴对称
D.平移
答案:1.A
2. 如图,要使设计出的图形是轴对称图形,适合放进图中虚线框内的是(

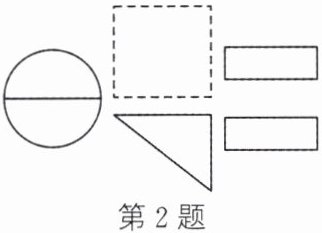
B
)

答案:2.B
3. (2025·龙东地区)我国古代有很多关于数学的伟大发现,其中包括很多美丽的图案,下列图形既是轴对称图形又是中心对称图形的为(
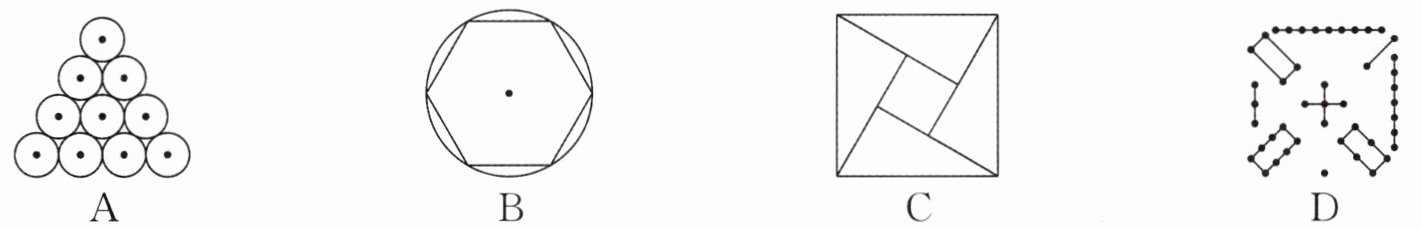
B
)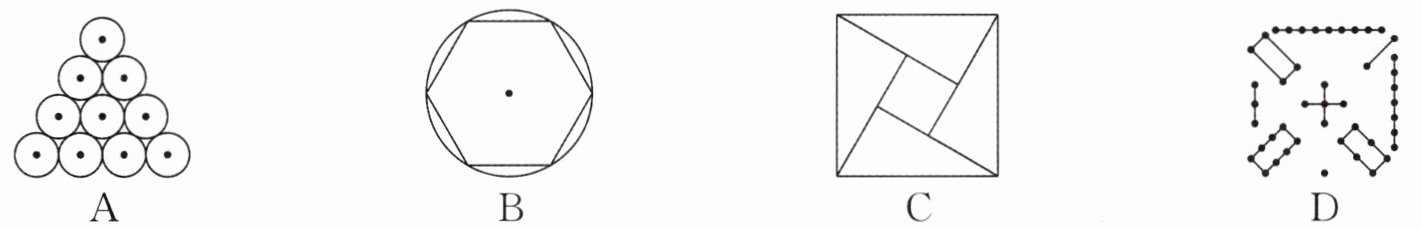
答案:3.B
4. 如图,将△ABC沿直线AB向右平移得到△BDE,连接CE.若△ABC的周长为9,四边形ADEC的周长为13,则平移的距离为(
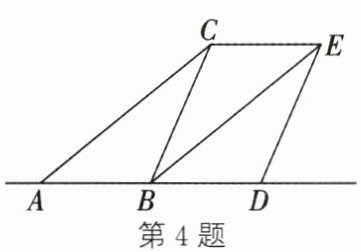
A.2
B.3
C.4
D.5
A
)
A.2
B.3
C.4
D.5
答案:4.A
解析:
证明:
∵△ABC沿直线AB向右平移得到△BDE,
∴平移距离为AB,AC=BE,BC=DE,AD=AB+BD=2AB。
∵△ABC的周长为9,
∴AB+BC+AC=9。
∵四边形ADEC的周长为13,
∴AD+DE+CE+AC=13。
∵AD=2AB,DE=BC,AC=BE,
∴2AB+BC+CE+AC=13,即AB+(AB+BC+AC)+CE=13。
∴AB+9+CE=13,得AB+CE=4。
∵四边形BDEC中,BC=DE,BE=AC,且平移性质知BE//AC,
∴四边形BDEC为平行四边形,
∴CE=BD=AB。
∴AB+AB=4,即2AB=4,AB=2。
A
∵△ABC沿直线AB向右平移得到△BDE,
∴平移距离为AB,AC=BE,BC=DE,AD=AB+BD=2AB。
∵△ABC的周长为9,
∴AB+BC+AC=9。
∵四边形ADEC的周长为13,
∴AD+DE+CE+AC=13。
∵AD=2AB,DE=BC,AC=BE,
∴2AB+BC+CE+AC=13,即AB+(AB+BC+AC)+CE=13。
∴AB+9+CE=13,得AB+CE=4。
∵四边形BDEC中,BC=DE,BE=AC,且平移性质知BE//AC,
∴四边形BDEC为平行四边形,
∴CE=BD=AB。
∴AB+AB=4,即2AB=4,AB=2。
A
5. (2025·甘肃)如图①,有三根木条a,b,c,∠1=80°,∠2=110°,固定木条b,c,将木条a绕点A顺时针转动至如图②所示的位置,使木条a与木条b平行,则可将木条a旋转(
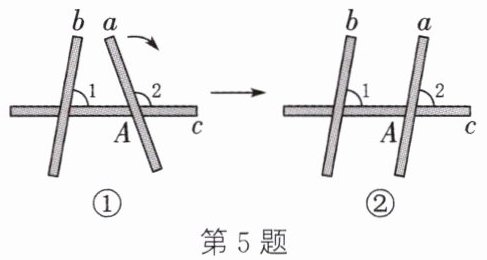
A.30°
B.40°
C.60°
D.80°
A
)
A.30°
B.40°
C.60°
D.80°
答案:5.A
6. 如图,直线x⊥y,直线x,y交于点O,点B,C,E在直线y上.若OC=1 cm,AC=2 cm,则直角三角形ODE可以看作是由直角三角形ABC经过某种图形变换得到的,这种变换方式可以为(
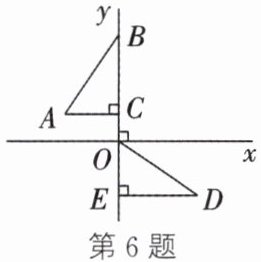
A.绕点C顺时针旋转90°,再向下平移3 cm
B.绕点C顺时针旋转90°,再向下平移1 cm
C.绕点C逆时针旋转90°,再向下平移1 cm
D.绕点C逆时针旋转90°,再向下平移3 cm
A
)
A.绕点C顺时针旋转90°,再向下平移3 cm
B.绕点C顺时针旋转90°,再向下平移1 cm
C.绕点C逆时针旋转90°,再向下平移1 cm
D.绕点C逆时针旋转90°,再向下平移3 cm
答案:6.A 解析:
∵直角三角形ODE是由直角三角形ABC经过某种图形变换得到的,
∴AC=OE=2cm.
∵CE=OC+OE=1+2=3(cm),
∴先将直角三角形ABC绕点C顺时针旋转90°,再向下平移3cm可得到直角三角形ODE.
∵直角三角形ODE是由直角三角形ABC经过某种图形变换得到的,
∴AC=OE=2cm.
∵CE=OC+OE=1+2=3(cm),
∴先将直角三角形ABC绕点C顺时针旋转90°,再向下平移3cm可得到直角三角形ODE.
7. 如图,△ABC与△CDA关于点O对称,过点O作一直线EF分别交AD,BC于点E,F.有下列结论:①点E和点F,点B和点D分别关于点O对称;②直线BD必经过点O;③△AOE与△COF成中心对称;④四边形DEOC与四边形BFOA的面积必相等.其中,正确的个数为(
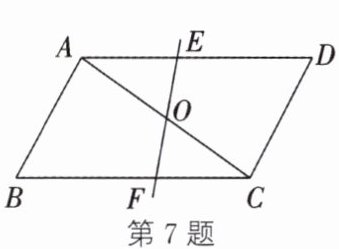
A.1
B.2
C.3
D.4
D
)
A.1
B.2
C.3
D.4
答案:7.D
解析:
证明:
∵△ABC与△CDA关于点O对称,
∴点O是对称中心,A与C、B与D关于O对称,故②正确;
∵AD、BC是对应线段,EF过O交AD于E、BC于F,
∴E与F关于O对称,故①正确;
∵A与C、E与F关于O对称,
∴△AOE与△COF关于O成中心对称,故③正确;
∵对称图形面积相等,S△AOD=S△COB,S△AOE=S△COF,
∴S四边形DEOC=S△AOD-S△AOE+S△COD,
S四边形BFOA=S△COB-S△COF+S△AOB,
又S△COD=S△AOB,
∴面积相等,故④正确.
综上,①②③④均正确,正确个数为4.
D
∵△ABC与△CDA关于点O对称,
∴点O是对称中心,A与C、B与D关于O对称,故②正确;
∵AD、BC是对应线段,EF过O交AD于E、BC于F,
∴E与F关于O对称,故①正确;
∵A与C、E与F关于O对称,
∴△AOE与△COF关于O成中心对称,故③正确;
∵对称图形面积相等,S△AOD=S△COB,S△AOE=S△COF,
∴S四边形DEOC=S△AOD-S△AOE+S△COD,
S四边形BFOA=S△COB-S△COF+S△AOB,
又S△COD=S△AOB,
∴面积相等,故④正确.
综上,①②③④均正确,正确个数为4.
D