14. 某公园的门票是每人$5$元,一次购买门票满$40$张,每张门票可优惠$1$元.若少于$40$人,则一个团队至少要有
33
人进公园,买$40$张门票反而合算.答案:14.33 解析:设$x$人进公园.根据题意,得$5x > 40 × (5 - 1)$,解得$x > 32$。又$\because x$为整数,$\therefore x$的最小值为$33$。
15. 解不等式组$\begin{cases}-2x\leqslant 6①,\\x > - 2②,\\3(x - 1) < x + 1③.\end{cases}$请结合题意,完成本题的解答.
(1)解不等式①,得
(2)解不等式③,得
(3)把不等式①②③的解集在如图所示的数轴上表示出来;
(4)从图中可以找出三个不等式的解集的公共部分,得不等式组的解集为

(1)解不等式①,得
$x \geq -3$
,依据是不等式的基本性质2
;(2)解不等式③,得
$x < 2$
;(3)把不等式①②③的解集在如图所示的数轴上表示出来;
(4)从图中可以找出三个不等式的解集的公共部分,得不等式组的解集为
$-2 < x < 2$
.
答案:
15.(1)$x \geq -3$ 不等式的基本性质2 (2)$x < 2$ (3)如图所示 (4)$-2 < x < 2$
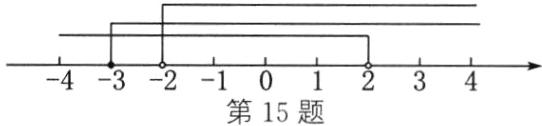
15.(1)$x \geq -3$ 不等式的基本性质2 (2)$x < 2$ (3)如图所示 (4)$-2 < x < 2$

16. 解下面的不等式(组):
(1)$5 - 2x < \dfrac{1 - x}{2}$;
(2)$\dfrac{2 - x}{2}\leqslant \dfrac{2x - 4}{3} < \dfrac{x - 1}{2}$.
(1)$5 - 2x < \dfrac{1 - x}{2}$;
(2)$\dfrac{2 - x}{2}\leqslant \dfrac{2x - 4}{3} < \dfrac{x - 1}{2}$.
答案:16.(1)$x > 3$ (2)$2 \leq x < 5$
解析:
16. 解:
(1)$5 - 2x < \dfrac{1 - x}{2}$
两边同乘2得:$10 - 4x < 1 - x$
移项得:$-4x + x < 1 - 10$
合并同类项得:$-3x < -9$
系数化为1得:$x > 3$
(2)$\dfrac{2 - x}{2}\leqslant \dfrac{2x - 4}{3} < \dfrac{x - 1}{2}$
解不等式$\dfrac{2 - x}{2}\leqslant \dfrac{2x - 4}{3}$
两边同乘6得:$3(2 - x) \leqslant 2(2x - 4)$
去括号得:$6 - 3x \leqslant 4x - 8$
移项得:$-3x - 4x \leqslant -8 - 6$
合并同类项得:$-7x \leqslant -14$
系数化为1得:$x \geqslant 2$
解不等式$\dfrac{2x - 4}{3} < \dfrac{x - 1}{2}$
两边同乘6得:$2(2x - 4) < 3(x - 1)$
去括号得:$4x - 8 < 3x - 3$
移项得:$4x - 3x < -3 + 8$
合并同类项得:$x < 5$
综上,不等式组的解集为$2 \leq x < 5$
(1)$5 - 2x < \dfrac{1 - x}{2}$
两边同乘2得:$10 - 4x < 1 - x$
移项得:$-4x + x < 1 - 10$
合并同类项得:$-3x < -9$
系数化为1得:$x > 3$
(2)$\dfrac{2 - x}{2}\leqslant \dfrac{2x - 4}{3} < \dfrac{x - 1}{2}$
解不等式$\dfrac{2 - x}{2}\leqslant \dfrac{2x - 4}{3}$
两边同乘6得:$3(2 - x) \leqslant 2(2x - 4)$
去括号得:$6 - 3x \leqslant 4x - 8$
移项得:$-3x - 4x \leqslant -8 - 6$
合并同类项得:$-7x \leqslant -14$
系数化为1得:$x \geqslant 2$
解不等式$\dfrac{2x - 4}{3} < \dfrac{x - 1}{2}$
两边同乘6得:$2(2x - 4) < 3(x - 1)$
去括号得:$4x - 8 < 3x - 3$
移项得:$4x - 3x < -3 + 8$
合并同类项得:$x < 5$
综上,不等式组的解集为$2 \leq x < 5$
17. 若不等式组$\begin{cases}2x + a > 0,\\\dfrac{1}{2}x > -\dfrac{a}{4} + 1\end{cases}$的解集中的任意$x$都能使不等式$x - 5 > 0$成立,求$a$的取值范围.
答案:$\begin{cases} 2x + a > 0 ① \\ \frac{1}{2}x > -\frac{a}{4} + 1 ② \end{cases}$
解不等式①,得$x > -\frac{a}{2}$。解不等式②,得$x > -\frac{a}{2} + 2$。$\therefore$原不等式组的解集为$x > -\frac{a}{2} + 2$。$\because$不等式$x - 5 > 0$的解集是$x > 5$,$\therefore -\frac{1}{2}a + 2 \geq 5$,解得$a \leq -6$,$\therefore a$的取值范围是$a \leq -6$
解不等式①,得$x > -\frac{a}{2}$。解不等式②,得$x > -\frac{a}{2} + 2$。$\therefore$原不等式组的解集为$x > -\frac{a}{2} + 2$。$\because$不等式$x - 5 > 0$的解集是$x > 5$,$\therefore -\frac{1}{2}a + 2 \geq 5$,解得$a \leq -6$,$\therefore a$的取值范围是$a \leq -6$
18. 定义$x$,$y$的新运算:$x※y = ax + by - 3$($a$,$b$为常数),等式的右侧是通常的混合运算.已知$2※1 = - 2$,$( - 1)※2 = 4$.
(1)求$3※( - 6)$的值;
(2)若$m$满足$\begin{cases}(4m - 2)※(2m + 3) > 6,\\(2m + 3)※(4m - 2) < 6,\end{cases}$求整数$m$的值.
(1)求$3※( - 6)$的值;
(2)若$m$满足$\begin{cases}(4m - 2)※(2m + 3) > 6,\\(2m + 3)※(4m - 2) < 6,\end{cases}$求整数$m$的值.
答案:18.(1)根据题意,得$\begin{cases} 2a + b - 3 = -2 \\ -a + 2b - 3 = 4 \end{cases}$,解得$\begin{cases} a = -1 \\ b = 3 \end{cases}$,$\therefore x ※ y = -x + 3y - 3$,$\therefore 3 ※ (-6) = -3 + 3 × (-6) - 3 = -24$
(2)$\because \begin{cases} (4m - 2) ※ (2m + 3) > 6 \\ (2m + 3) ※ (4m - 2) < 6 \end{cases}$,$\therefore \begin{cases} -(4m - 2) + 3(2m + 3) - 3 > 6 ① \\ -(2m + 3) + 3(4m - 2) - 3 < 6 ② \end{cases}$。由①,得$m > -1$,由②,得$m < 1.8$,$\therefore -1 < m < 1.8$,$\therefore$整数$m$的值为$0,1$
(2)$\because \begin{cases} (4m - 2) ※ (2m + 3) > 6 \\ (2m + 3) ※ (4m - 2) < 6 \end{cases}$,$\therefore \begin{cases} -(4m - 2) + 3(2m + 3) - 3 > 6 ① \\ -(2m + 3) + 3(4m - 2) - 3 < 6 ② \end{cases}$。由①,得$m > -1$,由②,得$m < 1.8$,$\therefore -1 < m < 1.8$,$\therefore$整数$m$的值为$0,1$