1. 下列命题属于真命题的是(
A.内错角相等
B.若 $ a^{10}=b^{10} $,则 $ a = b $
C.任意多边形的内角和为 $ 360^{\circ} $
D.等角的补角相等
D
)A.内错角相等
B.若 $ a^{10}=b^{10} $,则 $ a = b $
C.任意多边形的内角和为 $ 360^{\circ} $
D.等角的补角相等
答案:1.D
2. 能说明命题“对于任何数 $ a $,$ |a| > -a $”是假命题的一个反例可以为(
A.$ a = -2 $
B.$ a = \frac{1}{3} $
C.$ a = 1 $
D.$ a = 1.414213562··· $
A
)A.$ a = -2 $
B.$ a = \frac{1}{3} $
C.$ a = 1 $
D.$ a = 1.414213562··· $
答案:2.A
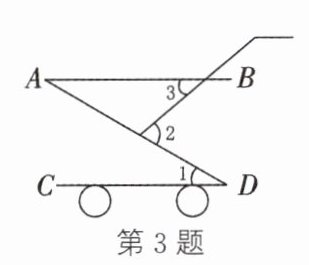
3. (2025·烟台)如图所示为一款儿童小推车的示意图,若 $ AB // CD $,$ \angle 1 = 30^{\circ} $,$ \angle 2 = 70^{\circ} $,则 $ \angle 3 $的度数为(
A.$ 40^{\circ} $
B.$ 35^{\circ} $
C.$ 30^{\circ} $
D.$ 20^{\circ} $
A
)
A.$ 40^{\circ} $
B.$ 35^{\circ} $
C.$ 30^{\circ} $
D.$ 20^{\circ} $
答案:3.A
解析:
延长BE交CD于点F,
因为AB//CD,∠1=30°,
所以∠EFD=∠1=30°,
因为∠2是△EFD的外角,∠2=70°,
所以∠2=∠EFD+∠3,
即70°=30°+∠3,
所以∠3=40°。
A
因为AB//CD,∠1=30°,
所以∠EFD=∠1=30°,
因为∠2是△EFD的外角,∠2=70°,
所以∠2=∠EFD+∠3,
即70°=30°+∠3,
所以∠3=40°。
A
4. 一个多边形的内角和与它的外角和的比为 $ 7:2 $,则这个多边形的边数为(
A.9
B.8
C.7
D.6
A
)A.9
B.8
C.7
D.6
答案:4.A
解析:
设这个多边形的边数为$n$。
多边形内角和公式为$(n - 2)×180°$,任意多边形外角和为$360°$。
由题意得$\frac{(n - 2)×180°}{360°} = \frac{7}{2}$
化简得$\frac{n - 2}{2} = \frac{7}{2}$
解得$n - 2 = 7$,$n = 9$
A
多边形内角和公式为$(n - 2)×180°$,任意多边形外角和为$360°$。
由题意得$\frac{(n - 2)×180°}{360°} = \frac{7}{2}$
化简得$\frac{n - 2}{2} = \frac{7}{2}$
解得$n - 2 = 7$,$n = 9$
A
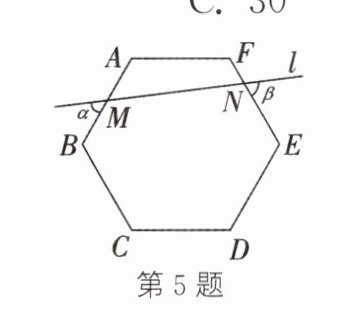
5. (2024·河北)如图,直线 $ l $ 与正六边形 $ ABCDEF $ 的边 $ AB $,$ EF $ 分别相交于点 $ M $,$ N $,则 $ \angle \alpha + \angle \beta $的度数为(
A.$ 115^{\circ} $
B.$ 120^{\circ} $
C.$ 135^{\circ} $
D.$ 144^{\circ} $
B
)
A.$ 115^{\circ} $
B.$ 120^{\circ} $
C.$ 135^{\circ} $
D.$ 144^{\circ} $
答案:5.B 解析:
∵正六边形每个内角的度数均为$\frac{(6 - 2) × 180^{\circ}}{6} =120^{\circ}$,
∴$\angle A + \angle F = 120^{\circ} + 120^{\circ} = 240^{\circ}$.
∵四边形$AMNF$的内角和为$(4 - 2) × 180^{\circ} = 360^{\circ}$,
∴$\angle AMN + \angle FNM = 360^{\circ} -240^{\circ} = 120^{\circ}$.根据对顶角相等,得$\angle\alpha + \angle\beta = 120^{\circ}$.
∵正六边形每个内角的度数均为$\frac{(6 - 2) × 180^{\circ}}{6} =120^{\circ}$,
∴$\angle A + \angle F = 120^{\circ} + 120^{\circ} = 240^{\circ}$.
∵四边形$AMNF$的内角和为$(4 - 2) × 180^{\circ} = 360^{\circ}$,
∴$\angle AMN + \angle FNM = 360^{\circ} -240^{\circ} = 120^{\circ}$.根据对顶角相等,得$\angle\alpha + \angle\beta = 120^{\circ}$.
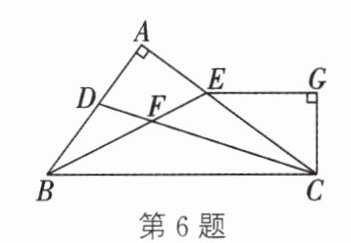
6. 如图,在 $ \triangle ABC $ 中,$ \angle A = 90^{\circ} $,$ BE $,$ CD $ 分别平分 $ \angle ABC $,$ \angle ACB $,且相交于点 $ F $,$ EG // BC $,$ CG ⊥ EG $ 于点 $ G $. 有下列结论:① $ \angle CEG = 2 \angle DCA $;② $ CA $ 平分 $ \angle BCG $;③ $ \angle ADC = \angle GCD $;④ $ \angle DFB = \frac{1}{2} \angle A $;⑤ $ \angle DFE = 135^{\circ} $. 其中,正确结论的个数为(
A.2
B.3
C.4
D.5
C
)
A.2
B.3
C.4
D.5
答案:6.C 解析:
∵$CD$平分$\angle ACB$,
∴$\angle ACB = 2\angle DCA$,$\angle ACD = \angle BCD$.
∵$EG // BC$,
∴$\angle CEG = \angle ACB = 2\angle DCA$.故结论①正确.
∵$\angle A = 90^{\circ}$,$CG ⊥ EG$,$EG // BC$,
∴$\angle ADC +\angle ACD = 90^{\circ}$,$CG ⊥ BC$,即$\angle BCG = 90^{\circ}$,
∴$\angle GCD + \angle BCD =90^{\circ}$.又
∵$\angle BCD = \angle ACD$,
∴$\angle ADC = \angle GCD$.故结论③正确.
∵$\angle A = 90^{\circ}$,
∴$\angle ABC + \angle ACB = 90^{\circ}$.
∵$BE$,$CD$分别平分$\angle ABC$,$\angle ACB$,
∴$\angle FBC = \frac{1}{2}\angle ABC$,$\angle FCB = \frac{1}{2}\angle ACB$,
∴$\angle BFC = 180^{\circ} - \frac{1}{2}(\angle ABC + \angle ACB) = 135^{\circ}$,
∴$\angle DFB =180^{\circ} - \angle BFC = 45^{\circ}$,
∴$\angle DFB = \frac{1}{2}\angle A$.故结论④正确.
∵$\angle BFC = 135^{\circ}$,
∴$\angle DFE = \angle BFC = 135^{\circ}$.故结论⑤正确.根据现有条件,无法推出$CA$平分$\angle BCG$,故结论②错误.综上所述,正确的结论的个数为4.
∵$CD$平分$\angle ACB$,
∴$\angle ACB = 2\angle DCA$,$\angle ACD = \angle BCD$.
∵$EG // BC$,
∴$\angle CEG = \angle ACB = 2\angle DCA$.故结论①正确.
∵$\angle A = 90^{\circ}$,$CG ⊥ EG$,$EG // BC$,
∴$\angle ADC +\angle ACD = 90^{\circ}$,$CG ⊥ BC$,即$\angle BCG = 90^{\circ}$,
∴$\angle GCD + \angle BCD =90^{\circ}$.又
∵$\angle BCD = \angle ACD$,
∴$\angle ADC = \angle GCD$.故结论③正确.
∵$\angle A = 90^{\circ}$,
∴$\angle ABC + \angle ACB = 90^{\circ}$.
∵$BE$,$CD$分别平分$\angle ABC$,$\angle ACB$,
∴$\angle FBC = \frac{1}{2}\angle ABC$,$\angle FCB = \frac{1}{2}\angle ACB$,
∴$\angle BFC = 180^{\circ} - \frac{1}{2}(\angle ABC + \angle ACB) = 135^{\circ}$,
∴$\angle DFB =180^{\circ} - \angle BFC = 45^{\circ}$,
∴$\angle DFB = \frac{1}{2}\angle A$.故结论④正确.
∵$\angle BFC = 135^{\circ}$,
∴$\angle DFE = \angle BFC = 135^{\circ}$.故结论⑤正确.根据现有条件,无法推出$CA$平分$\angle BCG$,故结论②错误.综上所述,正确的结论的个数为4.
7. (新情境·现实生活)某班甲、乙、丙、丁四名学生参加安全知识竞赛,在竞赛结果公布前,地理老师预测冠军是甲或乙;历史老师预测冠军是丙;政治老师预测冠军不可能是甲或丁;语文老师预测冠军是丁,而班主任老师看到竞赛结果后说以上有且只有两位老师说对了,则冠军是(
A.甲
B.乙
C.丙
D.丁
C
)A.甲
B.乙
C.丙
D.丁
答案:7.C 解析:
∵地理老师的话与其他三位老师的话都有矛盾,且有且只有两位老师说对了,
∴地理老师的话一定是错误的.
∵冠军只有一个,
∴历史老师和语文老师的话不能都对,则政治老师的话一定是正确的.又
∵与政治老师的话没有矛盾的是历史老师,
∴只有历史老师和政治老师的话是正确的.故冠军一定是丙.
∵地理老师的话与其他三位老师的话都有矛盾,且有且只有两位老师说对了,
∴地理老师的话一定是错误的.
∵冠军只有一个,
∴历史老师和语文老师的话不能都对,则政治老师的话一定是正确的.又
∵与政治老师的话没有矛盾的是历史老师,
∴只有历史老师和政治老师的话是正确的.故冠军一定是丙.
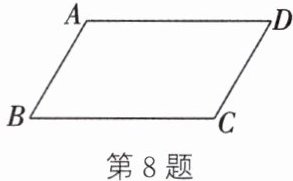
8. 如图,在四边形 $ ABCD $ 中,$ AB // CD $,$ \angle B = 60^{\circ} $,则当 $ \angle D = $
60
$ ^{\circ} $时,$ AD // BC $.
答案:8.60
9. (2025·北京改编)能说明命题“若 $ a^{2} > 4b^{2} $,则 $ a > 2b $”是假命题的一组有理数 $ a $,$ b $ 的值为 $ a = $
-3
,$ b = $1
.答案:9.答案不唯一,如$-3$ $1$
10. 一个多边形的外角和是内角和的 $ \frac{2}{9} $,则这个多边形的边数为
11
.答案:10.11
解析:
设这个多边形的边数为$n$。
多边形内角和公式为$(n - 2)×180°$,任意多边形外角和为$360°$。
由题意得:$360° = \frac{2}{9}×(n - 2)×180°$
化简得:$360 = \frac{2}{9}×180×(n - 2)$
$360 = 40×(n - 2)$
$n - 2 = 9$
$n = 11$
11
多边形内角和公式为$(n - 2)×180°$,任意多边形外角和为$360°$。
由题意得:$360° = \frac{2}{9}×(n - 2)×180°$
化简得:$360 = \frac{2}{9}×180×(n - 2)$
$360 = 40×(n - 2)$
$n - 2 = 9$
$n = 11$
11
11. 如图,在 $ \triangle ABC $ 中,$ BC = 6 \mathrm{ cm} $,射线 $ AG // BC $,点 $ E $ 从点 $ A $ 出发,沿射线 $ AG $ 以 $ 2 \mathrm{ cm/s} $ 的速度运动. 点 $ E $ 出发 $ 1 \mathrm{ s} $ 后,点 $ F $ 也从点 $ B $ 出发,沿射线 $ BC $ 以 $ 3.5 \mathrm{ cm/s} $ 的速度运动,连接 $ AF $,$ CE $. 设点 $ E $ 运动的时间为 $ t \mathrm{ s} $,其中 $ t > 0 $. 当 $ t = $
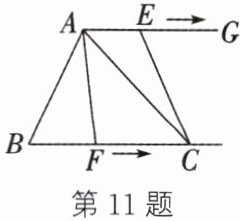
$\frac{19}{11}$或$\frac{19}{3}$
时,$ S_{\triangle ACE} = S_{\triangle AFC} $.
答案:11.$\frac{19}{11}$或$\frac{19}{3}$
解析:
解:设点$A$到$BC$的距离为$h$。
点$E$运动时间为$t\ \mathrm{s}$,则$AE = 2t\ \mathrm{cm}$。
点$F$比$E$晚出发$1\ \mathrm{s}$,运动时间为$(t - 1)\ \mathrm{s}$,则$BF = 3.5(t - 1)\ \mathrm{cm}$,$FC = |BC - BF| = |6 - 3.5(t - 1)|\ \mathrm{cm}$。
$S_{\triangle ACE} = \frac{1}{2} · AE · h = \frac{1}{2} · 2t · h = th$。
$S_{\triangle AFC} = \frac{1}{2} · FC · h = \frac{1}{2} · |6 - 3.5(t - 1)| · h$。
由$S_{\triangle ACE} = S_{\triangle AFC}$,得$th = \frac{1}{2} · |6 - 3.5(t - 1)| · h$,即$2t = |6 - 3.5(t - 1)|$。
分两种情况:
1. $6 - 3.5(t - 1) \geq 0$,即$t \leq \frac{19}{7}$时,$2t = 6 - 3.5(t - 1)$,解得$t = \frac{19}{11}$。
2. $6 - 3.5(t - 1) < 0$,即$t > \frac{19}{7}$时,$2t = 3.5(t - 1) - 6$,解得$t = \frac{19}{3}$。
综上,$t = \frac{19}{11}$或$\frac{19}{3}$。
$\frac{19}{11}$或$\frac{19}{3}$
点$E$运动时间为$t\ \mathrm{s}$,则$AE = 2t\ \mathrm{cm}$。
点$F$比$E$晚出发$1\ \mathrm{s}$,运动时间为$(t - 1)\ \mathrm{s}$,则$BF = 3.5(t - 1)\ \mathrm{cm}$,$FC = |BC - BF| = |6 - 3.5(t - 1)|\ \mathrm{cm}$。
$S_{\triangle ACE} = \frac{1}{2} · AE · h = \frac{1}{2} · 2t · h = th$。
$S_{\triangle AFC} = \frac{1}{2} · FC · h = \frac{1}{2} · |6 - 3.5(t - 1)| · h$。
由$S_{\triangle ACE} = S_{\triangle AFC}$,得$th = \frac{1}{2} · |6 - 3.5(t - 1)| · h$,即$2t = |6 - 3.5(t - 1)|$。
分两种情况:
1. $6 - 3.5(t - 1) \geq 0$,即$t \leq \frac{19}{7}$时,$2t = 6 - 3.5(t - 1)$,解得$t = \frac{19}{11}$。
2. $6 - 3.5(t - 1) < 0$,即$t > \frac{19}{7}$时,$2t = 3.5(t - 1) - 6$,解得$t = \frac{19}{3}$。
综上,$t = \frac{19}{11}$或$\frac{19}{3}$。
$\frac{19}{11}$或$\frac{19}{3}$