1. 如图,下列4个作图中,属于平移作图的有(
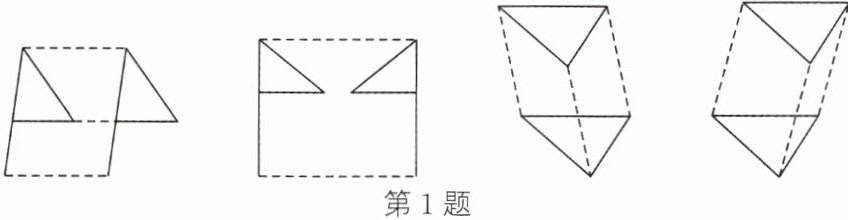
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:1.C
2. 如图,将△ABC沿BC向右平移得到△DEF.若BC=5,BE=2,则CF的长为(
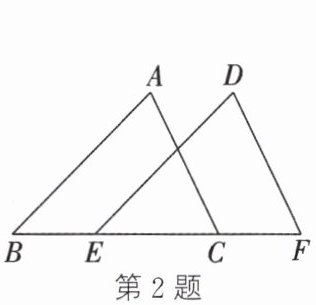
A.2
B.2.5
C.3
D.5
A
)
A.2
B.2.5
C.3
D.5
答案:2.A
解析:
证明:
∵△ABC沿BC向右平移得到△DEF,
∴BC=EF,
∵BC=5,
∴EF=5,
∵BE=2,BC=5,
∴EC=BC-BE=5-2=3,
∴CF=EF-EC=5-3=2.
答案:A
∵△ABC沿BC向右平移得到△DEF,
∴BC=EF,
∵BC=5,
∴EF=5,
∵BE=2,BC=5,
∴EC=BC-BE=5-2=3,
∴CF=EF-EC=5-3=2.
答案:A
3. 将字母“N”沿着某一方向平移一定的距离的作图中,第一步是在字母上找出关键的
4
个点.答案:3.4
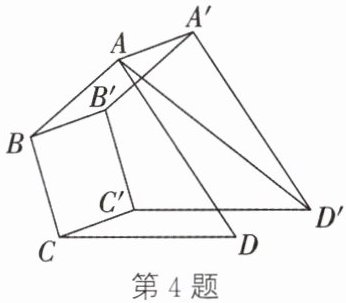
4. 如图,四边形A'B'C'D'是由四边形ABCD平移得到的.
(1)若BB'=3,AD=7,则AD'长的取值范围是
(2)分别连接CC',AA',则CC'与AA'的关系为
(1)若BB'=3,AD=7,则AD'长的取值范围是
4<AD'<10
;(2)分别连接CC',AA',则CC'与AA'的关系为
平行且相等
.
答案:4.(1)4<AD'<10 (2)平行且相等
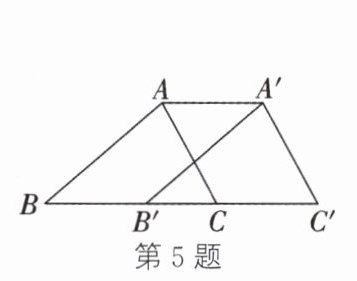
5. 如图,将△ABC沿BC方向平移,A',B'分别是点A,B的对应点,且BB'=3,连接AA'.若四边形ABC'A'的周长为16,则△ABC的周长是
10
.
答案:5.10
解析:
解:
∵△ABC沿BC方向平移得到△A'B'C',
∴AA'=BB'=3,A'B'=AB,A'C'=AC,B'C'=BC。
∵BB'=3,
∴CC'=BB'=3。
∵四边形ABC'A'的周长为16,
∴AB+BC+CC'+A'C'+A'A=16,
即AB+BC+3+AC+3=16,
∴AB+BC+AC=10,
即△ABC的周长是10。
10
∵△ABC沿BC方向平移得到△A'B'C',
∴AA'=BB'=3,A'B'=AB,A'C'=AC,B'C'=BC。
∵BB'=3,
∴CC'=BB'=3。
∵四边形ABC'A'的周长为16,
∴AB+BC+CC'+A'C'+A'A=16,
即AB+BC+3+AC+3=16,
∴AB+BC+AC=10,
即△ABC的周长是10。
10
6. 如图,将△ABC沿BC方向平移得到△DEF.
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
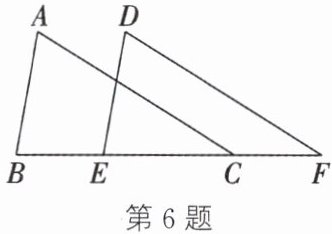
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.

答案:6.(1)因为△DEF由△ABC沿BC方向平移得到,所以∠ACB=∠F=32°.又因为∠B=80°,所以∠A=180°-32°-80°=68° (2)由平移可知,EF=BC,所以EF-EC=BC-EC,即CF=BE.又因为BC=5,EC=3,所以BE=BC-EC=5-3=2,所以CF=BE=2
解析:
(1)
∵△DEF由△ABC沿BC方向平移得到,
∴∠ACB=∠F=32°。
∵∠B=80°,
∴∠A=180°-∠B-∠ACB=180°-80°-32°=68°。
(2)
∵△DEF由△ABC沿BC方向平移得到,
∴EF=BC=5。
∵EC=3,
∴CF=EF-EC=5-3=2。
∵△DEF由△ABC沿BC方向平移得到,
∴∠ACB=∠F=32°。
∵∠B=80°,
∴∠A=180°-∠B-∠ACB=180°-80°-32°=68°。
(2)
∵△DEF由△ABC沿BC方向平移得到,
∴EF=BC=5。
∵EC=3,
∴CF=EF-EC=5-3=2。
7. 如图,在△ABC中,∠BAC=90°,把△ABC沿着直线BC向右平移5 cm后得到△DEF,连接AE,AD.有下列结论:① AC//DF;② ∠ADE=∠DEF;③ CF=5 cm;④ DE⊥AC.其中,正确的有(
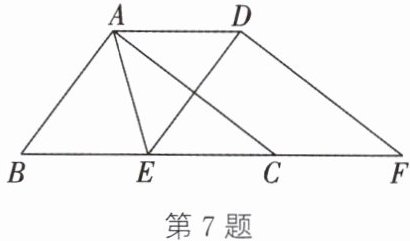
A.1个
B.2个
C.3个
D.4个
D
)
A.1个
B.2个
C.3个
D.4个
答案:7.D
解析:
证明:
∵△ABC沿着直线BC向右平移5cm后得到△DEF,
∴AC//DF,AC=DF,AD//CF,AD=CF=5cm,∠BAC=∠EDF=90°,AB//DE,AB=DE,
∴①AC//DF正确;③CF=5cm正确;
∵AD//CF,AB//DE,
∴∠ADE=∠DEF(两直线平行,内错角相等),故②正确;
∵∠BAC=90°,AB//DE,
∴DE⊥AC,故④正确。
综上,正确的有①②③④,共4个。
答案:D
∵△ABC沿着直线BC向右平移5cm后得到△DEF,
∴AC//DF,AC=DF,AD//CF,AD=CF=5cm,∠BAC=∠EDF=90°,AB//DE,AB=DE,
∴①AC//DF正确;③CF=5cm正确;
∵AD//CF,AB//DE,
∴∠ADE=∠DEF(两直线平行,内错角相等),故②正确;
∵∠BAC=90°,AB//DE,
∴DE⊥AC,故④正确。
综上,正确的有①②③④,共4个。
答案:D