1. 下列图形中,可以由其中一个图形平移得到的是(
 ]
]
B
) ]
]答案:1. B
2. 如图,△ABC 是直角三角形,∠ABC = 90°,将其沿直角边 BC 所在的直线向右平移得到△DEF.下列结论中,不一定成立的是(
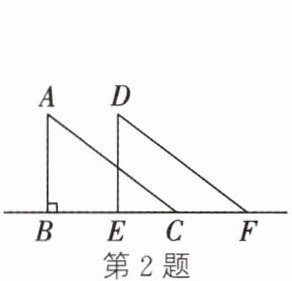
A.△ABC 与△DEF 的形状、大小完全相同
B.∠A + ∠DFE = 90°
C.AC // DF 且 AC = DF
D.EC = CF
D
)
A.△ABC 与△DEF 的形状、大小完全相同
B.∠A + ∠DFE = 90°
C.AC // DF 且 AC = DF
D.EC = CF
答案:2. D
解析:
证明:
选项A:平移不改变图形的形状和大小,故△ABC与△DEF的形状、大小完全相同,A成立。
选项B:由平移性质得∠DFE=∠ACB,在Rt△ABC中,∠A+∠ACB=90°,则∠A+∠DFE=90°,B成立。
选项C:平移后对应线段平行且相等,故AC//DF且AC=DF,C成立。
选项D:平移距离不确定,EC与CF不一定相等,D不一定成立。
D
选项A:平移不改变图形的形状和大小,故△ABC与△DEF的形状、大小完全相同,A成立。
选项B:由平移性质得∠DFE=∠ACB,在Rt△ABC中,∠A+∠ACB=90°,则∠A+∠DFE=90°,B成立。
选项C:平移后对应线段平行且相等,故AC//DF且AC=DF,C成立。
选项D:平移距离不确定,EC与CF不一定相等,D不一定成立。
D
3. (新考法·结论开放题)我国的汉字博大精深,奥妙无穷。“圭”“羽”等一些汉字可以看作是通过平移变换得到的,请你再写一个此类型的汉字:
答案不唯一,如朋
。答案:3. 答案不唯一,如朋
4. 如图所示为将一块边长为 50 cm 的正方形材料剪掉一部分而得到的垫片,现测得 FG = 8 cm,则这块垫片的周长是
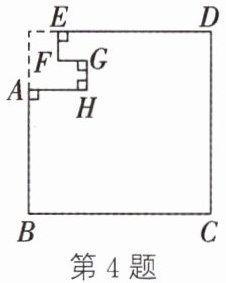
216
cm。
答案:4. 216
解析:
解:通过平移线段可知,垫片的周长等于原正方形周长加上$2FG$。
原正方形边长为$50\,\mathrm{cm}$,周长为$4×50 = 200\,\mathrm{cm}$。
$FG = 8\,\mathrm{cm}$,故额外增加的长度为$2×8 = 16\,\mathrm{cm}$。
垫片周长为$200 + 16 = 216\,\mathrm{cm}$。
216
原正方形边长为$50\,\mathrm{cm}$,周长为$4×50 = 200\,\mathrm{cm}$。
$FG = 8\,\mathrm{cm}$,故额外增加的长度为$2×8 = 16\,\mathrm{cm}$。
垫片周长为$200 + 16 = 216\,\mathrm{cm}$。
216
5. 如图,∠3 = 38°,直线 b 平移后得到直线 a,则∠1 + ∠2 =
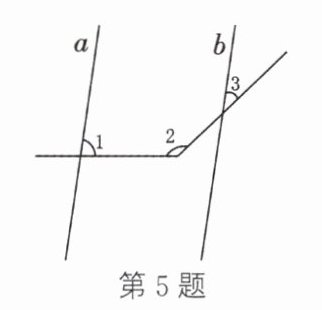
218
°。
答案:5. 218
解析:
解:过∠2的顶点作直线c平行于直线a,
因为直线b平移后得到直线a,所以a//b,
所以a//b//c,
所以∠1+∠4=180°(两直线平行,同旁内角互补),
∠3=∠5=38°(两直线平行,内错角相等),
因为∠2=∠4+∠5,
所以∠1+∠2=∠1+∠4+∠5=180°+38°=218°。
故答案为:218
因为直线b平移后得到直线a,所以a//b,
所以a//b//c,
所以∠1+∠4=180°(两直线平行,同旁内角互补),
∠3=∠5=38°(两直线平行,内错角相等),
因为∠2=∠4+∠5,
所以∠1+∠2=∠1+∠4+∠5=180°+38°=218°。
故答案为:218
6. 如图,C 是线段 AB 平移后点 A 的对应点,画出线段 AB 平移后的图形。请将下面的画法补充完整。
(1)画法 1:连接 AC,过点 B 向下画线段 BD,使 BD 满足
(2)画法 2:过点 C 向下画线段 CD,使 CD 满足
 ]
]
(1)画法 1:连接 AC,过点 B 向下画线段 BD,使 BD 满足
BD//AC,BD=AC
;连接 CD,则 CD 即为所求。(2)画法 2:过点 C 向下画线段 CD,使 CD 满足
CD//AB,CD=AB
,则 CD 即为所求。 ]
]答案:6. (1) BD//AC,BD=AC (2) CD//AB,CD=AB
7. 在如图所示的方格纸中,△ABC 的顶点均在方格纸的格点上,则在方格纸中与△ABC 成轴对称的格点三角形共有(
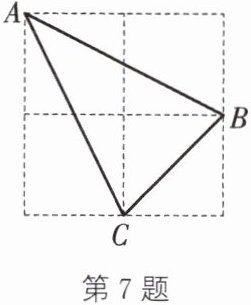
A.1 个
B.2 个
C.3 个
D.4 个
C
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:7. C
解析:
在方格纸中,分别以水平、竖直及两条对角线方向为对称轴进行分析:
水平方向对称轴:可得到1个与△ABC成轴对称的格点三角形;
竖直方向对称轴:可得到1个与△ABC成轴对称的格点三角形;
对角线方向对称轴:可得到1个与△ABC成轴对称的格点三角形。
共3个。
C
水平方向对称轴:可得到1个与△ABC成轴对称的格点三角形;
竖直方向对称轴:可得到1个与△ABC成轴对称的格点三角形;
对角线方向对称轴:可得到1个与△ABC成轴对称的格点三角形。
共3个。
C