18. (整体思想)“整体思想”是中学数学解题过程中的一种重要的思想方法,常常用这样的方法把复杂的问题转化为简单问题.
例如:已知方程组 $\begin{cases}a - 2ab + b = 1,\\2a + ab + 2b = -3,\end{cases}$ 求 $a + b$,$ab$ 的值.
解:原方程组即为 $\begin{cases}a + b - 2ab = 1,\\2(a + b)+ab = -3.\end{cases}$ 设 $a + b = x$,$ab = y$.
原方程组可变形为 $\begin{cases}x - 2y = 1,\\2x + y = -3,\end{cases}$ 解得 $\begin{cases}x = -1,\\y = -1,\end{cases}$ 即 $\begin{cases}a + b = -1,\\ab = -1.\end{cases}$
理解上述内容,解决下列问题:
(1)若关于 $x$ 的一元一次方程 $ax + b = 2x(a,b$ 为常数,且 $a ≠ 2)$ 的解为 $x = -4$,则关于 $y$ 的一元一次方程 $a(y - 9)+b = 2y - 18$ 的解为 $y =$
(2)已知关于 $m$,$n$ 的方程组 $\begin{cases}3m - 2mn - 6n = -9,\\2m + mn - 4n = 1,\end{cases}$ 求 $m + 2n$ 的值;
(3)已知关于 $a$,$b$,$c$ 的方程组 $\begin{cases}3a - b + 9c = -34,\\-2a + 4b - 11c = 16,\end{cases}$ 求 $a + b + c$ 的值.
例如:已知方程组 $\begin{cases}a - 2ab + b = 1,\\2a + ab + 2b = -3,\end{cases}$ 求 $a + b$,$ab$ 的值.
解:原方程组即为 $\begin{cases}a + b - 2ab = 1,\\2(a + b)+ab = -3.\end{cases}$ 设 $a + b = x$,$ab = y$.
原方程组可变形为 $\begin{cases}x - 2y = 1,\\2x + y = -3,\end{cases}$ 解得 $\begin{cases}x = -1,\\y = -1,\end{cases}$ 即 $\begin{cases}a + b = -1,\\ab = -1.\end{cases}$
理解上述内容,解决下列问题:
(1)若关于 $x$ 的一元一次方程 $ax + b = 2x(a,b$ 为常数,且 $a ≠ 2)$ 的解为 $x = -4$,则关于 $y$ 的一元一次方程 $a(y - 9)+b = 2y - 18$ 的解为 $y =$
5
;(2)已知关于 $m$,$n$ 的方程组 $\begin{cases}3m - 2mn - 6n = -9,\\2m + mn - 4n = 1,\end{cases}$ 求 $m + 2n$ 的值;
(3)已知关于 $a$,$b$,$c$ 的方程组 $\begin{cases}3a - b + 9c = -34,\\-2a + 4b - 11c = 16,\end{cases}$ 求 $a + b + c$ 的值.
答案:18. (1)5 (2)将原方程组整理,得\begin{cases}3(m - 2n) - 2mn = - 9, \\ 2(m - 2n) + mn = 1. \end{cases}设$p = m - 2n$,$q = mn$,则该方程组化为\begin{cases}3p - 2q = - 9, \\ 2p + q = 1, \end{cases}解得\begin{cases}p = - 1, \\ q = 3, \end{cases}即$m - 2n = - 1$,$mn = 3$.所以$(m + 2n)^2 = (m - 2n)^2 + 8mn = (-1)^2 + 8×3 = 25$,则$m + 2n = \pm5$ (3)设$a + b + c = k(3a - b + 9c) + t(-2a + 4b - 11c)$,整理,得$a + b + c = (3k - 2t)a + (4t - k)b + (9k - 11t)c$.所以\begin{cases}3k - 2t = 1, \\ 4t - k = 1, \\ 9k - 11t = 1. \end{cases}解得\begin{cases}k = 0.6, \\ t = 0.4, \end{cases}此时$9k - 11t = 1$,符合题意.因为\begin{cases}3a - b + 9c = - 34, \\ -2a + 4b - 11c = 16, \end{cases}所以$a + b + c = 0.6×(-34) + 0.4×16 = -14$
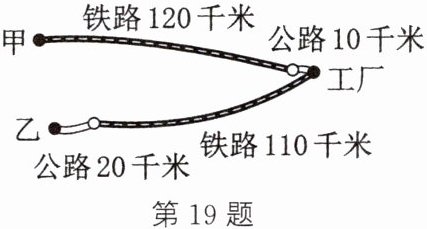
19. 如图,某工厂与甲、乙两地由公路、铁路相连.这家工厂从甲地购买一批每吨 $1000$ 元的原料运回工厂,制成每吨 $8000$ 元的产品运到乙地.已知公路的运价为 $1.5$ 元/(吨·千米),铁路的运价为 $1.2$ 元/(吨·千米),且这两次运输共支出公路运输费 $15000$ 元,铁路运输费 $97200$ 元.
(1)该工厂从甲地购买了多少吨原料? 制成运往乙地的产品有多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
(1)该工厂从甲地购买了多少吨原料? 制成运往乙地的产品有多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?

答案:19. (1)设该工厂从甲地购买了$x$吨原料,制成运往乙地的产品有$y$吨.根据题意,得\begin{cases}1.2x·120 + 1.2y·110 = 97200, \\ 1.5x·10 + 1.5y·20 = 15000, \end{cases}解得\begin{cases}x = 400, \\ y = 300. \end{cases}答:该工厂从甲地购买了400吨原料,制成运往乙地的产品有300吨 (2)$300×8000 - 1000×400 - 15000 - 97200 = 1887800(元)$,答:这批产品的销售款比原料费与运输费的和多1887800元