1. (2024·内江)不等式 $3x \geq x - 4$ 的解集是(
A.$x \geq - 2$
B.$x \leq - 2$
C.$x > - 2$
D.$x < - 2$
A
)A.$x \geq - 2$
B.$x \leq - 2$
C.$x > - 2$
D.$x < - 2$
答案:1.A
解析:
解:$3x \geq x - 4$
$3x - x \geq -4$
$2x \geq -4$
$x \geq -2$
A
$3x - x \geq -4$
$2x \geq -4$
$x \geq -2$
A
2. 不等式 $2x + 1 > 3$ 的解集在数轴上表示正确的是(
]
B
)
]
答案:2.B
解析:
解:$2x + 1 > 3$
$2x > 3 - 1$
$2x > 2$
$x > 1$
在数轴上表示为从1出发向右的射线,1处为空心圆圈,对应选项B。
B
$2x > 3 - 1$
$2x > 2$
$x > 1$
在数轴上表示为从1出发向右的射线,1处为空心圆圈,对应选项B。
B
3. (1) 不等式 $\frac{1}{2}x - 1 > 0$ 的解集为
(2) 不等式 $2x + 3 \geq - 5$ 的解集为
(3) 不等式 $2 - 3x \leq x$ 的解集为
x>2
;(2) 不等式 $2x + 3 \geq - 5$ 的解集为
$x\geqslant-4$
;(3) 不等式 $2 - 3x \leq x$ 的解集为
$x\geqslant\frac{1}{2}$
.答案:$3.(1)x>2 (2)x\geqslant-4 (3)x\geqslant\frac{1}{2}$
4. 解下列不等式,并把它们的解集在数轴上表示出来:
(1) $3x - 2 > x$;
(2) $2x - 4 < 10$;
(3) $- 2x - 3 \geq 2$;
(4) $\frac{2}{3}x + \frac{1}{2} \geq \frac{1}{2}x$.
(1) $3x - 2 > x$;
(2) $2x - 4 < 10$;
(3) $- 2x - 3 \geq 2$;
(4) $\frac{2}{3}x + \frac{1}{2} \geq \frac{1}{2}x$.
答案:
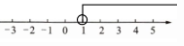
(1)解:$3x - 2 > x$
$3x - x > 2$
$2x > 2$
$x > 1$
(2)解:$2x - 4 < 10$
$2x < 10 + 4$
$2x < 14$
$x < 7$

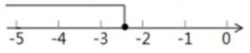
(3)解:$-2x - 3 \geq 2$
$-2x \geq 2 + 3$
$-2x \geq 5$
$x \leq -\frac{5}{2}$
(4)解:$\frac{2}{3}x + \frac{1}{2} \geq \frac{1}{2}x$
$\frac{2}{3}x - \frac{1}{2}x \geq -\frac{1}{2}$
$\frac{4}{6}x - \frac{3}{6}x \geq -\frac{1}{2}$
$\frac{1}{6}x \geq -\frac{1}{2}$
$x \geq -3$

(1)解:$3x - 2 > x$
$3x - x > 2$
$2x > 2$
$x > 1$

(2)解:$2x - 4 < 10$
$2x < 10 + 4$
$2x < 14$
$x < 7$

(3)解:$-2x - 3 \geq 2$
$-2x \geq 2 + 3$
$-2x \geq 5$
$x \leq -\frac{5}{2}$

(4)解:$\frac{2}{3}x + \frac{1}{2} \geq \frac{1}{2}x$
$\frac{2}{3}x - \frac{1}{2}x \geq -\frac{1}{2}$
$\frac{4}{6}x - \frac{3}{6}x \geq -\frac{1}{2}$
$\frac{1}{6}x \geq -\frac{1}{2}$
$x \geq -3$

5. 若关于 $x$ 的一元一次方程 $x - m + 2 = 0$ 的解是负数,则 $m$ 的取值范围是(
A.$m \geq 2$
B.$m > 2$
C.$m < 2$
D.$m \leq 2$
C
)A.$m \geq 2$
B.$m > 2$
C.$m < 2$
D.$m \leq 2$
答案:5.C
解析:
解:解方程$x - m + 2 = 0$,得$x = m - 2$。
因为方程的解是负数,所以$m - 2 < 0$,解得$m < 2$。
C
因为方程的解是负数,所以$m - 2 < 0$,解得$m < 2$。
C
6. (2024·宁夏)已知 $|3 - a| = a - 3$,则 $a$ 的取值范围在数轴上表示正确的是(
]
A
)
]
答案:6.A
解析:
因为$|3 - a| = a - 3$,根据绝对值的性质,当$|x| = y$且$y \geq 0$时,$x \leq 0$,所以$3 - a \leq 0$,解得$a \geq 3$。在数轴上表示为从3出发向右的射线,且3处为实心点,对应选项A。
A
A
7. 若不等式 $ax - 2 > 0$ 的解集为 $x < - 2$,则关于 $y$ 的方程 $ay + 2 = 0$ 的解为(
A.$y = - 1$
B.$y = 1$
C.$y = - 2$
D.$y = 2$
D
)A.$y = - 1$
B.$y = 1$
C.$y = - 2$
D.$y = 2$
答案:7.D
解析:
解:解不等式$ax - 2 > 0$,得$ax > 2$。
因为解集为$x < -2$,所以$a < 0$,且$\frac{2}{a} = -2$,解得$a = -1$。
将$a = -1$代入方程$ay + 2 = 0$,得$-y + 2 = 0$,解得$y = 2$。
D
因为解集为$x < -2$,所以$a < 0$,且$\frac{2}{a} = -2$,解得$a = -1$。
将$a = -1$代入方程$ay + 2 = 0$,得$-y + 2 = 0$,解得$y = 2$。
D