8. 若不等式 $(m - 1)x > (m - 1)$ 两边同除以 $(m - 1)$,得 $x < 1$,则 $m$ 的取值范围是
m<1
.答案:8.m<1
9. 对于任意数 $m$ 和 $n$,规定一种新运算:$m※n = m^{2}n - mn - 3n$.例如:$1※2 = 1^{2}×2 - 1×2 - 3×2 = - 6$.若 $3※k \geq - 6$,则 $k$ 的取值范围是
$k\geqslant-2$
.答案:$9.k\geqslant-2 $解析:根据题意,得$3※k = 3^{2}× k - 3k - 3k = 3k,$所以$3※k\geqslant-6 $可化为$3k\geqslant-6,$解得$k\geqslant-2.$
解析:
$3※k = 3^{2}k - 3k - 3k = 9k - 3k - 3k = 3k$,
因为$3※k \geq - 6$,
所以$3k \geq - 6$,
解得$k \geq - 2$。
因为$3※k \geq - 6$,
所以$3k \geq - 6$,
解得$k \geq - 2$。
10. 解下列不等式,并把它们的解集在数轴上表示出来:
(1) (2024·广西)$7x + 5 < 5x + 1$;
(2) $10x - 4 < 12x + 5$;
(3) $\frac{1}{4}x - 3 \leq \frac{9}{4}x - 4$;
(4) $- 2x + 1 > \frac{3x}{4} - 10$.
(1) (2024·广西)$7x + 5 < 5x + 1$;
(2) $10x - 4 < 12x + 5$;
(3) $\frac{1}{4}x - 3 \leq \frac{9}{4}x - 4$;
(4) $- 2x + 1 > \frac{3x}{4} - 10$.
答案:
(1)解:$7x + 5 < 5x + 1$
$7x - 5x < 1 - 5$
$2x < -4$
$x < -2$

(2)解:$10x - 4 < 12x + 5$
$10x - 12x < 5 + 4$
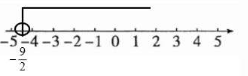
$-2x < 9$
$x > -\frac{9}{2}$
(3)解:$\frac{1}{4}x - 3 \leq \frac{9}{4}x - 4$
$\frac{1}{4}x - \frac{9}{4}x \leq -4 + 3$
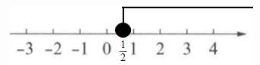
$-2x \leq -1$
$x \geq \frac{1}{2}$
(4)解:$-2x + 1 > \frac{3x}{4} - 10$
$-2x - \frac{3x}{4} > -10 - 1$
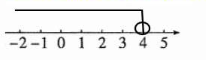
$-\frac{11x}{4} > -11$
$x < 4$
(1)解:$7x + 5 < 5x + 1$
$7x - 5x < 1 - 5$
$2x < -4$
$x < -2$

(2)解:$10x - 4 < 12x + 5$
$10x - 12x < 5 + 4$
$-2x < 9$
$x > -\frac{9}{2}$

(3)解:$\frac{1}{4}x - 3 \leq \frac{9}{4}x - 4$
$\frac{1}{4}x - \frac{9}{4}x \leq -4 + 3$
$-2x \leq -1$
$x \geq \frac{1}{2}$

(4)解:$-2x + 1 > \frac{3x}{4} - 10$
$-2x - \frac{3x}{4} > -10 - 1$
$-\frac{11x}{4} > -11$
$x < 4$

11. 如图,在数轴上点 $A$,$B$ 分别表示数 $1$,$- 2x + 3$.
(1) 求 $x$ 的取值范围.
(2) 数轴上表示数 $- x + 2$ 的点应落在(
A. 点 $A$ 的左边
B. 线段 $AB$ 上
C. 点 $B$ 的右边
 ]
]
(1) 求 $x$ 的取值范围.
(2) 数轴上表示数 $- x + 2$ 的点应落在(
B
)A. 点 $A$ 的左边
B. 线段 $AB$ 上
C. 点 $B$ 的右边
 ]
]答案:11.(1)根据数轴上的点表示的数右边的总比左边的大,得-2x + 3>1,解得x<1
(2)B 解析:①因为x<1,所以-x>-1,-x + 2>-1 + 2,即-x + 2>1,所以数轴上表示数-x + 2的点在点A的右边。
②作差,得-2x + 3 - (-x + 2) = -x + 1. 因为x<1,所以-x>-1,所以-x + 1>0,所以-2x + 3 - (-x + 2)>0,即-2x + 3>-x + 2,所以数轴上表示数-x + 2的点在点B的左边。综上所述,数轴上表示数-x + 2的点应落在线段AB上。也可以采用“特殊值法”求解,如取x = 0.
(2)B 解析:①因为x<1,所以-x>-1,-x + 2>-1 + 2,即-x + 2>1,所以数轴上表示数-x + 2的点在点A的右边。
②作差,得-2x + 3 - (-x + 2) = -x + 1. 因为x<1,所以-x>-1,所以-x + 1>0,所以-2x + 3 - (-x + 2)>0,即-2x + 3>-x + 2,所以数轴上表示数-x + 2的点在点B的左边。综上所述,数轴上表示数-x + 2的点应落在线段AB上。也可以采用“特殊值法”求解,如取x = 0.
12. 已知关于 $x$ 的方程 $3(x - 2a) + 2 = x - a + 1$ 的解适合不等式 $2x - 10 > 8a$,求 $a$ 的取值范围.
答案:解:解方程$3(x - 2a) + 2 = x - a + 1$,
去括号得:$3x - 6a + 2 = x - a + 1$,
移项得:$3x - x = -a + 1 + 6a - 2$,
合并同类项得:$2x = 5a - 1$,
解得:$x = \frac{5a - 1}{2}$。
将$x = \frac{5a - 1}{2}$代入不等式$2x - 10 > 8a$,
得:$2×\frac{5a - 1}{2} - 10 > 8a$,
化简得:$5a - 1 - 10 > 8a$,
移项得:$5a - 8a > 1 + 10$,
合并同类项得:$-3a > 11$,
解得:$a < -\frac{11}{3}$。
去括号得:$3x - 6a + 2 = x - a + 1$,
移项得:$3x - x = -a + 1 + 6a - 2$,
合并同类项得:$2x = 5a - 1$,
解得:$x = \frac{5a - 1}{2}$。
将$x = \frac{5a - 1}{2}$代入不等式$2x - 10 > 8a$,
得:$2×\frac{5a - 1}{2} - 10 > 8a$,
化简得:$5a - 1 - 10 > 8a$,
移项得:$5a - 8a > 1 + 10$,
合并同类项得:$-3a > 11$,
解得:$a < -\frac{11}{3}$。