6. 解不等式$\frac{1 + 4x}{3} > x - 1$,下列在数轴上表示的解集正确的是(

D
)
答案:6.D
解析:
解:$\frac{1 + 4x}{3} > x - 1$
两边同乘3:$1 + 4x > 3(x - 1)$
去括号:$1 + 4x > 3x - 3$
移项:$4x - 3x > -3 - 1$
合并同类项:$x > -4$
解集在数轴上表示为:D
两边同乘3:$1 + 4x > 3(x - 1)$
去括号:$1 + 4x > 3x - 3$
移项:$4x - 3x > -3 - 1$
合并同类项:$x > -4$
解集在数轴上表示为:D
7. 不等式$\frac{x + 1}{3} > \frac{2x + 1}{2} - 1$的自然数解的个数是(
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:7.B
解析:
解:去分母,得$2(x + 1)>3(2x + 1)-6$,
去括号,得$2x + 2>6x + 3 - 6$,
移项,得$2x - 6x>3 - 6 - 2$,
合并同类项,得$-4x>-5$,
系数化为1,得$x<\frac{5}{4}$,
则不等式的自然数解为0,1,共2个。
B
去括号,得$2x + 2>6x + 3 - 6$,
移项,得$2x - 6x>3 - 6 - 2$,
合并同类项,得$-4x>-5$,
系数化为1,得$x<\frac{5}{4}$,
则不等式的自然数解为0,1,共2个。
B
8. 若添一个负整数$m$,使$-9$,$5$与$m$这三个数的平均数小于$m$,则$m$的值为
$-1$
.答案:8.$-1$ 解析:根据题意,得$\frac{-9 + 5 + m}{3}<m$,解得$m>-2$.因为$m$是负整数,所以$m=-1$.
解析:
根据题意,得$\frac{-9 + 5 + m}{3} < m$,
去分母,得$-9 + 5 + m < 3m$,
移项、合并同类项,得$-2m < 4$,
系数化为$1$,得$m > -2$,
因为$m$是负整数,所以$m = -1$。
$-1$
去分母,得$-9 + 5 + m < 3m$,
移项、合并同类项,得$-2m < 4$,
系数化为$1$,得$m > -2$,
因为$m$是负整数,所以$m = -1$。
$-1$
9. 已知关于$x$的不等式$\frac{1}{3}x - a \leq 0$有且只有三个非负整数解,则$a$的取值范围是
$\frac{2}{3}\leq a<1$
.答案:9.$\frac{2}{3}\leq a<1$
解析:
解:解不等式$\frac{1}{3}x - a \leq 0$,得$x \leq 3a$。
因为不等式有且只有三个非负整数解,所以非负整数解为$0$,$1$,$2$。
则$2 \leq 3a < 3$,解得$\frac{2}{3} \leq a < 1$。
$\frac{2}{3}\leq a<1$
因为不等式有且只有三个非负整数解,所以非负整数解为$0$,$1$,$2$。
则$2 \leq 3a < 3$,解得$\frac{2}{3} \leq a < 1$。
$\frac{2}{3}\leq a<1$
10. 解下列不等式,并把它们的解集在数轴上表示出来:
(1)$2x - 1 > \frac{3x - 1}{2}$;
(2)(2024·眉山)$\frac{x + 1}{3} - 1 \leq \frac{2 - x}{2}$;
(3)$1 - \frac{4x + 22}{9} \leq \frac{2x - 1}{3}$;
(4)$\frac{x}{2} - \frac{5x + 11}{6} > \frac{2x - 4}{3} - 1$.
(1)$2x - 1 > \frac{3x - 1}{2}$;
(2)(2024·眉山)$\frac{x + 1}{3} - 1 \leq \frac{2 - x}{2}$;
(3)$1 - \frac{4x + 22}{9} \leq \frac{2x - 1}{3}$;
(4)$\frac{x}{2} - \frac{5x + 11}{6} > \frac{2x - 4}{3} - 1$.
答案:
(1)解不等式$2x - 1 > \frac{3x - 1}{2}$
解:
去分母,两边同时乘以$2$得:$2(2x - 1)>3x - 1$。
去括号:$4x - 2>3x - 1$。
移项:$4x - 3x>-1 + 2$。
合并同类项:$x>1$。
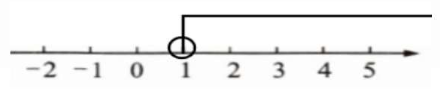
(2)解不等式$\frac{x + 1}{3} - 1 \leq \frac{2 - x}{2}$
解:
去分母,两边同时乘以$6$得:$2(x + 1) - 6\leq3(2 - x)$。
去括号:$2x + 2 - 6\leq6 - 3x$。
移项:$2x + 3x\leq6 + 6 - 2$。
合并同类项:$5x\leq10$。
系数化为$1$:$x\leq2$。

(3)解不等式$1 - \frac{4x + 22}{9} \leq \frac{2x - 1}{3}$
解:
去分母,两边同时乘以$9$得:$9 - (4x + 22)\leq3(2x - 1)$。
去括号:$9 - 4x - 22\leq6x - 3$。
移项:$-4x - 6x\leq-3 - 9 + 22$。
合并同类项:$-10x\leq10$。
系数化为$1$:$x\geq - 1$。

(4)解不等式$\frac{x}{2} - \frac{5x + 11}{6} > \frac{2x - 4}{3} - 1$
解:
去分母,两边同时乘以$6$得:$3x - (5x + 11)>2(2x - 4) - 6$。
去括号:$3x - 5x - 11>4x - 8 - 6$。
移项:$3x - 5x - 4x>-8 - 6 + 11$。
合并同类项:$-6x>-3$。
系数化为$1$:$x<\frac{1}{2}$。
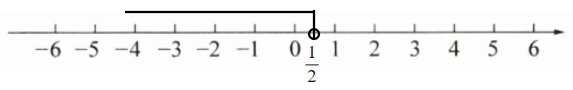
(1)解不等式$2x - 1 > \frac{3x - 1}{2}$
解:
去分母,两边同时乘以$2$得:$2(2x - 1)>3x - 1$。
去括号:$4x - 2>3x - 1$。
移项:$4x - 3x>-1 + 2$。
合并同类项:$x>1$。

(2)解不等式$\frac{x + 1}{3} - 1 \leq \frac{2 - x}{2}$
解:
去分母,两边同时乘以$6$得:$2(x + 1) - 6\leq3(2 - x)$。
去括号:$2x + 2 - 6\leq6 - 3x$。
移项:$2x + 3x\leq6 + 6 - 2$。
合并同类项:$5x\leq10$。
系数化为$1$:$x\leq2$。

(3)解不等式$1 - \frac{4x + 22}{9} \leq \frac{2x - 1}{3}$
解:
去分母,两边同时乘以$9$得:$9 - (4x + 22)\leq3(2x - 1)$。
去括号:$9 - 4x - 22\leq6x - 3$。
移项:$-4x - 6x\leq-3 - 9 + 22$。
合并同类项:$-10x\leq10$。
系数化为$1$:$x\geq - 1$。

(4)解不等式$\frac{x}{2} - \frac{5x + 11}{6} > \frac{2x - 4}{3} - 1$
解:
去分母,两边同时乘以$6$得:$3x - (5x + 11)>2(2x - 4) - 6$。
去括号:$3x - 5x - 11>4x - 8 - 6$。
移项:$3x - 5x - 4x>-8 - 6 + 11$。
合并同类项:$-6x>-3$。
系数化为$1$:$x<\frac{1}{2}$。
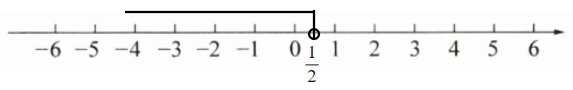
11. (2024·呼和浩特)
(1)解不等式:$\frac{2x - 1}{3} - 1 > \frac{x}{2}$;
(2)上述不等式的任意一个解都比关于$x$的不等式$2x - 1 \leq x + m$的解大,求$m$的取值范围.
(1)解不等式:$\frac{2x - 1}{3} - 1 > \frac{x}{2}$;
(2)上述不等式的任意一个解都比关于$x$的不等式$2x - 1 \leq x + m$的解大,求$m$的取值范围.
答案:11.(1)去分母,得$2(2x - 1)-6>3x$,去括号,得$4x - 2 - 6>3x$,移项、合并同类项,得$x>8$ (2)由$2x - 1\leq x + m$,得$x\leq m + 1$.根据题意,得$m + 1\leq8$,解得$m\leq7$,所以$m$的取值范围是$m\leq7$
12. 当$k < 6$时,方程$3(x - 1) = k$的解是不等式$4x - 1 < x + 2m$的解,求$m$的最小整数值.
答案:由方程$3(x - 1) = k$,得$x = \frac{k}{3} + 1$。
由不等式$4x - 1 \lt x + 2m$,得$3x \lt 2m + 1$,即$x \lt \frac{2m + 1}{3}$。
因为当$k \lt 6$时,方程$3(x - 1) = k$的解是不等式$4x - 1 \lt x + 2m$的解,
而当$k \lt 6$时,$x=\frac{k}{3}+1\lt\frac{6}{3}+1 = 3$,
所以$\frac{k}{3}+1\lt\frac{2m + 1}{3}$在$k \lt 6$时恒成立时,$3\leqslant\frac{2m + 1}{3}$,
$9\leqslant2m + 1$,
$2m\geqslant8$,
$m\geqslant4$。
所以$m$的最小整数值是$4$。
由不等式$4x - 1 \lt x + 2m$,得$3x \lt 2m + 1$,即$x \lt \frac{2m + 1}{3}$。
因为当$k \lt 6$时,方程$3(x - 1) = k$的解是不等式$4x - 1 \lt x + 2m$的解,
而当$k \lt 6$时,$x=\frac{k}{3}+1\lt\frac{6}{3}+1 = 3$,
所以$\frac{k}{3}+1\lt\frac{2m + 1}{3}$在$k \lt 6$时恒成立时,$3\leqslant\frac{2m + 1}{3}$,
$9\leqslant2m + 1$,
$2m\geqslant8$,
$m\geqslant4$。
所以$m$的最小整数值是$4$。