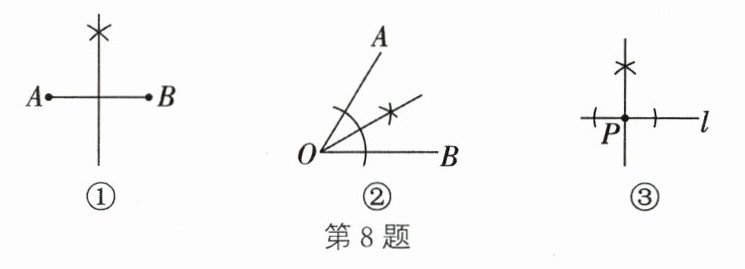
8. 如图,有下列三种尺规作图:① 作一条线段的垂直平分线;② 作一个角的平分线;③ 过直线上一点 $P$ 作直线 $l$ 的垂线. 其中,作法正确的个数是(
A.0
B.1
C.2
D.3
C
)
A.0
B.1
C.2
D.3
答案:8.C
解析:
①作一条线段的垂直平分线,需分别以线段两端点为圆心,大于线段一半长度为半径画弧,两弧交于两点,过两点作直线,图①未体现两弧交点连线,作法错误;
②作一个角的平分线,以顶点为圆心画弧交两边于两点,再分别以两点为圆心画弧交于一点,过顶点和交点作射线,图②符合,作法正确;
③过直线上一点$P$作直线$l$的垂线,需以$P$为圆心,适当长度为半径画弧交直线于两点,再分别以两点为圆心画弧交于一点,过$P$和交点作直线,图③符合,作法正确。
正确的个数是2。
C
②作一个角的平分线,以顶点为圆心画弧交两边于两点,再分别以两点为圆心画弧交于一点,过顶点和交点作射线,图②符合,作法正确;
③过直线上一点$P$作直线$l$的垂线,需以$P$为圆心,适当长度为半径画弧交直线于两点,再分别以两点为圆心画弧交于一点,过$P$和交点作直线,图③符合,作法正确。
正确的个数是2。
C
9. 将自己的双手手掌印按在同一张纸上,两个手掌印通过平移
不能
(填“能”或“不能”)完全重合在一起.答案:9.不能
10. 如图,正三角形 $ABC$(图①)与正三角形 $DEF$(图②)完全相同. 如果图①经过一次轴对称变换后得到图②,那么点 $A$,$B$,$C$ 的对应点分别是
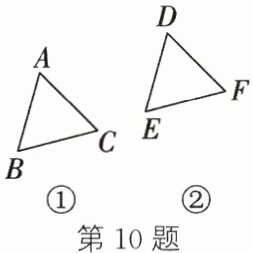
D,F,E
.
答案:10.D,F,E
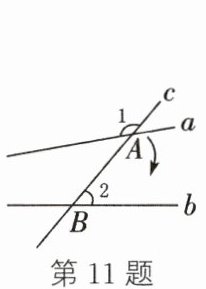
11. 如图,直线 $a$,$b$ 与直线 $c$ 分别相交于点 $A$,$B$. 若 $\angle 1 = 140^{\circ}$,$\angle 2 = 50^{\circ}$,要使 $a// b$,则直线 $a$ 绕点 $A$ 顺时针方向至少旋转
10
$^{\circ}$.
答案:11.10
解析:
解:当$a // b$时,设直线$a$旋转后与直线$c$相交形成的锐角为$\angle 3$,则$\angle 3 = \angle 2 = 50^{\circ}$。
因为$\angle 1 = 140^{\circ}$,所以$\angle 1$的邻补角为$180^{\circ} - 140^{\circ} = 40^{\circ}$。
直线$a$绕点$A$顺时针旋转的角度为$50^{\circ} - 40^{\circ} = 10^{\circ}$。
10
因为$\angle 1 = 140^{\circ}$,所以$\angle 1$的邻补角为$180^{\circ} - 140^{\circ} = 40^{\circ}$。
直线$a$绕点$A$顺时针旋转的角度为$50^{\circ} - 40^{\circ} = 10^{\circ}$。
10
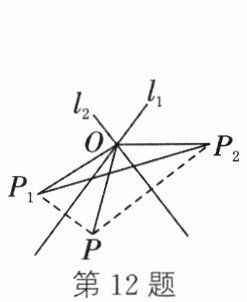
12. 如图,直线 $l_1$,$l_2$ 交于点 $O$,点 $P$ 关于 $l_1$,$l_2$ 的对称点分别为 $P_1$,$P_2$. 若 $OP = 8$,$P_1P_2 = 14$,则 $\triangle P_1OP_2$ 的周长是
30
.
答案:12.30
解析:
解:
∵点$P$关于$l_1$,$l_2$的对称点分别为$P_1$,$P_2$,
∴$OP_1 = OP$,$OP_2 = OP$。
∵$OP = 8$,
∴$OP_1 = OP_2 = 8$。
∵$P_1P_2 = 14$,
∴$\triangle P_1OP_2$的周长为$OP_1 + OP_2 + P_1P_2 = 8 + 8 + 14 = 30$。
30
∵点$P$关于$l_1$,$l_2$的对称点分别为$P_1$,$P_2$,
∴$OP_1 = OP$,$OP_2 = OP$。
∵$OP = 8$,
∴$OP_1 = OP_2 = 8$。
∵$P_1P_2 = 14$,
∴$\triangle P_1OP_2$的周长为$OP_1 + OP_2 + P_1P_2 = 8 + 8 + 14 = 30$。
30
13. 如图,将 $\triangle ABC$ 绕点 $A$ 顺时针旋转得到 $\triangle AB'C'$,点 $C'$ 恰好落在线段 $AB$ 上,连接 $BB'$. 若 $AC = 1$,$AB = 3$,则 $BC'$ 的长为
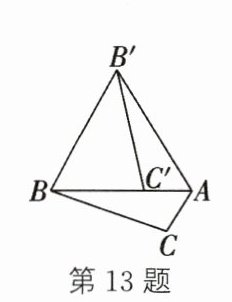
2
.
答案:13.2
解析:
解:由旋转性质得,$AC' = AC = 1$。
因为点$C'$在线段$AB$上,且$AB = 3$,
所以$BC' = AB - AC' = 3 - 1 = 2$。
故答案为:$2$。
因为点$C'$在线段$AB$上,且$AB = 3$,
所以$BC' = AB - AC' = 3 - 1 = 2$。
故答案为:$2$。
14. 将数字 $6$ 旋转 $180^{\circ}$ 得到数字 $9$,将数字 $9$ 旋转 $180^{\circ}$ 得到数字 $6$,现将数 $69$ 旋转 $180^{\circ}$ 得到的数是
69
.答案:14.69
15. 如图,在 $\triangle ABC$ 中,按图中尺规作图痕迹作射线 $BM$,交 $AC$ 于点 $E$,过点 $E$ 作 $DE// BC$,交 $AB$ 于点 $D$. 若 $\angle BDE = 122^{\circ}$,则 $\angle EBC$ 的度数为
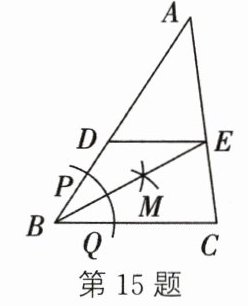
29°
.
答案:15.29°
解析:
解:
∵DE//BC,
∴∠BDE+∠DBC=180°(两直线平行,同旁内角互补)。
∵∠BDE=122°,
∴∠DBC=180°-122°=58°。
由尺规作图痕迹可知,BM平分∠DBC,
∴∠EBC=∠DBE=∠DBC/2=58°/2=29°。
故∠EBC的度数为29°。
∵DE//BC,
∴∠BDE+∠DBC=180°(两直线平行,同旁内角互补)。
∵∠BDE=122°,
∴∠DBC=180°-122°=58°。
由尺规作图痕迹可知,BM平分∠DBC,
∴∠EBC=∠DBE=∠DBC/2=58°/2=29°。
故∠EBC的度数为29°。
16. 如图,$\triangle ABC$ 与 $\triangle BCD$ 都是等边三角形. 有下列说法:① $\triangle BCD$ 可由 $\triangle ABC$ 绕点 $B$ 顺时针旋转 $60^{\circ}$ 得到,$A$ 与 $D$ 是一组对应点;② $\triangle BCD$ 可由 $\triangle ABC$ 绕点 $C$ 逆时针旋转 $60^{\circ}$ 得到,$B$ 与 $D$ 是一组对应点;③ $\triangle BCD$ 可由 $\triangle ABC$ 绕 $BC$ 的中点旋转 $180^{\circ}$ 得到,$B$ 与 $C$ 是一组对应点;④ $\triangle BCD$ 可由 $\triangle ABC$ 关于 $BC$ 作轴对称变换得到,$B$ 与 $C$ 是一组对应点. 其中,正确的有
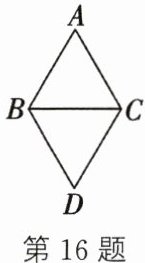
②③
(填序号).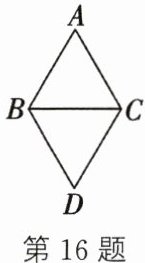
答案:16.②③
解析:
证明:①假设$\triangle BCD$由$\triangle ABC$绕点$B$顺时针旋转$60°$得到,$A$对应$D$,则$BA=BD$,$\angle ABD=60°$。但$\triangle ABC$是等边三角形,$BA=BC$,若$BD=BA=BC$,则$D$与$C$重合,与图中$D$位置矛盾,①错误。
②$\triangle ABC$与$\triangle BCD$均为等边三角形,$BC=BC$,$AC=CD$,$\angle ACB=\angle BCD=60°$。绕点$C$逆时针旋转$60°$,$A$对应$D$,$B$对应$B$,$\triangle ABC$与$\triangle BCD$重合,②正确。
③设$BC$中点为$O$,则$BO=CO$。绕$O$旋转$180°$,$B$与$C$互换,$A$与$D$关于$O$中心对称,$\triangle ABC$与$\triangle BCD$重合,③正确。
④关于$BC$轴对称,$A$与$D$应关于$BC$对称,此时$AB=BD$,$AC=CD$,但$\angle ABC=\angle DBC=60°$,则$D$在$AB$延长线上,与图中$D$位置不符,④错误。
正确的有②③。
②③
②$\triangle ABC$与$\triangle BCD$均为等边三角形,$BC=BC$,$AC=CD$,$\angle ACB=\angle BCD=60°$。绕点$C$逆时针旋转$60°$,$A$对应$D$,$B$对应$B$,$\triangle ABC$与$\triangle BCD$重合,②正确。
③设$BC$中点为$O$,则$BO=CO$。绕$O$旋转$180°$,$B$与$C$互换,$A$与$D$关于$O$中心对称,$\triangle ABC$与$\triangle BCD$重合,③正确。
④关于$BC$轴对称,$A$与$D$应关于$BC$对称,此时$AB=BD$,$AC=CD$,但$\angle ABC=\angle DBC=60°$,则$D$在$AB$延长线上,与图中$D$位置不符,④错误。
正确的有②③。
②③