1. 将一张正方形纸片按如图①所示的步骤沿虚线对折两次,然后沿图③中的虚线剪去一个角,则展开铺平后的图形大致是(

A
)
答案:1.A
2. 武术是我国传统的体育项目. 下列武术动作图形中,是轴对称图形的为(
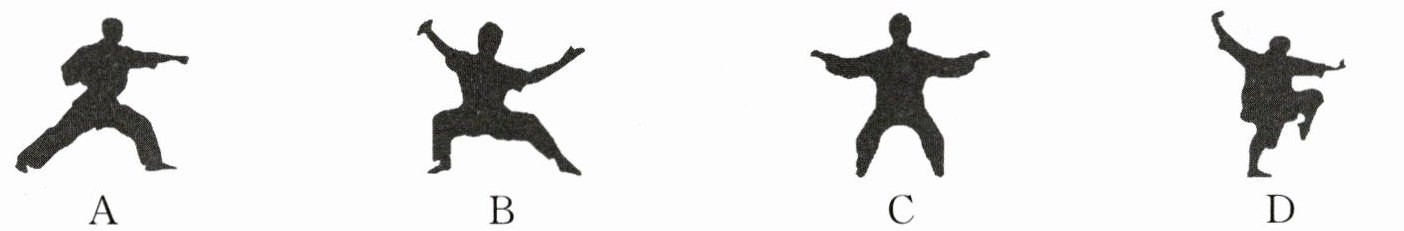
C
)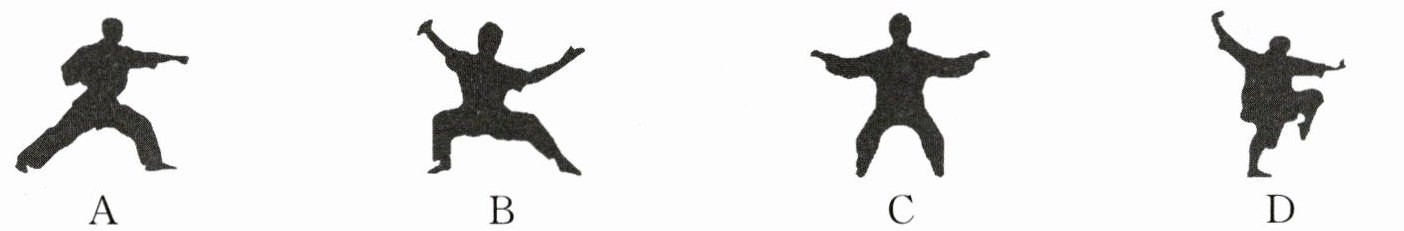
答案:2.C
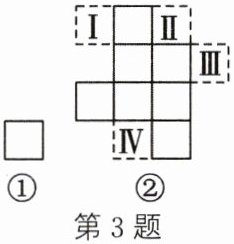
3. 如图,图①和图②中所有的小正方形都相同,将图①的小正方形放在图②中Ⅰ,Ⅱ,Ⅲ,Ⅳ的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是(
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
C
)
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
答案:3.C
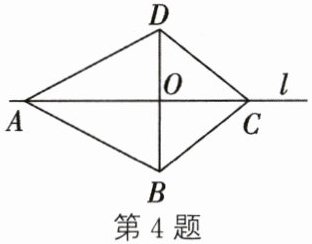
4. 如图,四边形 $ABCD$ 关于直线 $l$ 对称,有下列结论:① $AB// CD$;② $AC⊥ BD$;③ $AO = CO$;④ $AB⊥ BC$. 其中,一定正确的有(
A.①②
B.②③
C.①④
D.②
D
)
A.①②
B.②③
C.①④
D.②
答案:4.D
解析:
证明:
∵四边形$ABCD$关于直线$l$对称,直线$l$为$AC$所在直线,
∴$AC$垂直平分$BD$,
∴$AC⊥BD$,$BO=DO$,故②正确;
无法得出$AO=CO$,$AB/\!/CD$,$AB⊥BC$,故①③④错误。
一定正确的有②。
D
∵四边形$ABCD$关于直线$l$对称,直线$l$为$AC$所在直线,
∴$AC$垂直平分$BD$,
∴$AC⊥BD$,$BO=DO$,故②正确;
无法得出$AO=CO$,$AB/\!/CD$,$AB⊥BC$,故①③④错误。
一定正确的有②。
D
5. 如图,$C$,$E$ 是直线 $l$ 两侧的点,以点 $C$ 为圆心,$CE$ 的长为半径画弧交直线 $l$ 于 $A$,$B$ 两点,再分别以点 $A$,$B$ 为圆心,大于 $\frac{1}{2}AB$ 的长为半径画弧,两弧交于点 $D$,连接 $CA$,$CB$,$CD$,则下列结论不一定正确的是(
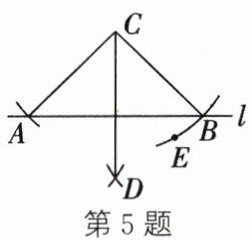
A.$CA = CB$
B.点 $C$,$D$ 关于直线 $l$ 对称
C.$CD⊥$ 直线 $l$
D.点 $A$,$B$ 关于直线 $CD$ 对称
B
)
A.$CA = CB$
B.点 $C$,$D$ 关于直线 $l$ 对称
C.$CD⊥$ 直线 $l$
D.点 $A$,$B$ 关于直线 $CD$ 对称
答案:5.B
解析:
解:由题意知,CA、CB都是以C为圆心,CE为半径的圆的半径,所以CA=CB,A正确;
分别以A、B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧交于点D,则点D在AB的垂直平分线上,又CA=CB,所以点C也在AB的垂直平分线上,因此CD是AB的垂直平分线,即CD⊥直线l,C正确;
因为CD是AB的垂直平分线,所以点A,B关于直线CD对称,D正确;
点C,D是否关于直线l对称取决于CD是否被直线l平分,由题意无法得出此结论,B不一定正确。
答案:B
分别以A、B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧交于点D,则点D在AB的垂直平分线上,又CA=CB,所以点C也在AB的垂直平分线上,因此CD是AB的垂直平分线,即CD⊥直线l,C正确;
因为CD是AB的垂直平分线,所以点A,B关于直线CD对称,D正确;
点C,D是否关于直线l对称取决于CD是否被直线l平分,由题意无法得出此结论,B不一定正确。
答案:B
6. 如图,$O$ 是正六边形 $ABCDEF$ 的中心,图中可以通过一次旋转与 $\triangle ABF$ 重合的三角形($\triangle ABF$ 自身除外)的个数是(
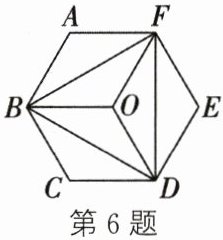
A.2
B.3
C.4
D.5
D
)
A.2
B.3
C.4
D.5
答案:6.D
解析:
证明:正六边形 $ABCDEF$ 绕中心 $O$ 旋转$60°$的整数倍可与自身重合。$\triangle ABF$ 绕 $O$ 顺时针旋转$60°$得$\triangle BCD$,旋转$120°$得$\triangle CDE$,旋转$180°$得$\triangle DEF$,旋转$240°$得$\triangle EFA$,旋转$300°$得$\triangle FAB$(自身)。除去自身,共5个。
D
D
7. 如图,关于这一图案的形成,下列说法正确的是(
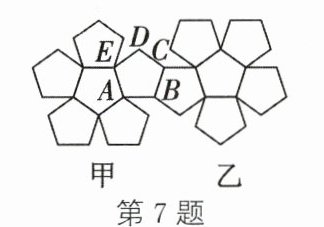
A.图案乙是由图案甲沿射线 $AB$ 方向平移 $3$ 个 $AB$ 长得到的
B.图案乙是由图案甲绕点 $C$ 旋转 $180^{\circ}$ 得到的
C.图案乙是由图案甲沿直线 $BC$ 翻折得到的
D.图案乙是由图案甲绕 $BC$ 的中点旋转 $180^{\circ}$ 得到的
D
)
A.图案乙是由图案甲沿射线 $AB$ 方向平移 $3$ 个 $AB$ 长得到的
B.图案乙是由图案甲绕点 $C$ 旋转 $180^{\circ}$ 得到的
C.图案乙是由图案甲沿直线 $BC$ 翻折得到的
D.图案乙是由图案甲绕 $BC$ 的中点旋转 $180^{\circ}$ 得到的
答案:7.D