20. (6 分)先化简,再求值:$ (x + 2y)(x - 2y) + (-x + 2y)^{2} $,其中 $ x = -1 $,$ y = \dfrac{1}{2} $.
答案:20.原式=$x^2 - 4y^2 + 4y^2 - 4xy + x^2 = 2x^2 - 4xy$.当$x = -1$,$y = \frac{1}{2}$时,原式=$2×(-1)^2 - 4×(-1)×\frac{1}{2} = 2×1 + 2 = 2 + 2 = 4$
解析:
解:原式$=(x + 2y)(x - 2y) + (-x + 2y)^{2}$
$=x^{2}-(2y)^{2}+(-x)^{2}+2×(-x)×2y+(2y)^{2}$
$=x^{2}-4y^{2}+x^{2}-4xy + 4y^{2}$
$=2x^{2}-4xy$
当$x = -1$,$y=\dfrac{1}{2}$时,
原式$=2×(-1)^{2}-4×(-1)×\dfrac{1}{2}$
$=2×1 + 2$
$=4$
$=x^{2}-(2y)^{2}+(-x)^{2}+2×(-x)×2y+(2y)^{2}$
$=x^{2}-4y^{2}+x^{2}-4xy + 4y^{2}$
$=2x^{2}-4xy$
当$x = -1$,$y=\dfrac{1}{2}$时,
原式$=2×(-1)^{2}-4×(-1)×\dfrac{1}{2}$
$=2×1 + 2$
$=4$
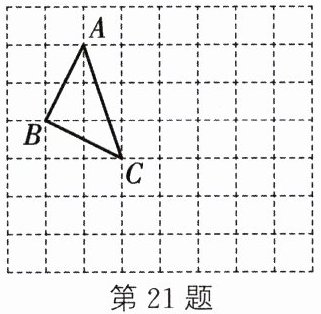
21. (6 分)用无刻度的直尺作图:如图,网格中每个小正方形的边长均为 1 个单位长度,$ \triangle ABC $ 的顶点均在小正方形的格点上.
(1)将 $ \triangle ABC $ 先向右平移 5 个单位长度,再向下平移 3 个单位长度得到 $ \triangle A_{1}B_{1}C_{1} $,画出 $ \triangle A_{1}B_{1}C_{1} $;
(2)将 $ \triangle ABC $ 绕点 $ C $ 顺时针旋转 $ 90^{\circ} $ 得到 $ \triangle A_{2}B_{2}C $,画出 $ \triangle A_{2}B_{2}C $;
(3)若(2)中的线段 $ CB_{2} $ 也可由(1)中的线段 $ A_{1}B_{1} $ 旋转得到,请作出其旋转中心 $ O $.
(1)将 $ \triangle ABC $ 先向右平移 5 个单位长度,再向下平移 3 个单位长度得到 $ \triangle A_{1}B_{1}C_{1} $,画出 $ \triangle A_{1}B_{1}C_{1} $;
(2)将 $ \triangle ABC $ 绕点 $ C $ 顺时针旋转 $ 90^{\circ} $ 得到 $ \triangle A_{2}B_{2}C $,画出 $ \triangle A_{2}B_{2}C $;
(3)若(2)中的线段 $ CB_{2} $ 也可由(1)中的线段 $ A_{1}B_{1} $ 旋转得到,请作出其旋转中心 $ O $.

答案:
21.(1)如图,$\triangle A_1B_1C_1$即为所求 (2)如图,$\triangle A_2B_2C$即为所求 (3)如图,点$O$即为所求
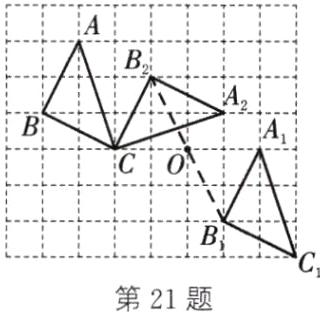
21.(1)如图,$\triangle A_1B_1C_1$即为所求 (2)如图,$\triangle A_2B_2C$即为所求 (3)如图,点$O$即为所求

22. (6 分)已知 $ a $ 是一个正整数,且 $ a $ 除以 3 余 1,试说明:$ a^{2} + 4a + 4 $ 能被 9 整除.
答案:22.因为$a$是一个正整数,且$a$除以$3$余$1$,所以设$a = 3x + 1$($x$是非负整数),所以$a^2 + 4a + 4 = (a + 2)^2 = (3x + 3)^2 = 9(x + 1)^2$.因为$(x + 1)^2$是正整数,所以$9(x + 1)^2$能被$9$整除,所以$a^2 + 4a + 4$能被$9$整除
解析:
因为$a$是正整数,且$a$除以$3$余$1$,设$a = 3x + 1$($x$是非负整数)。
$a^2 + 4a + 4 = (a + 2)^2$,将$a = 3x + 1$代入得:
$(3x + 1 + 2)^2 = (3x + 3)^2 = [3(x + 1)]^2 = 9(x + 1)^2$
因为$(x + 1)^2$是正整数,所以$9(x + 1)^2$能被$9$整除,即$a^2 + 4a + 4$能被$9$整除。
$a^2 + 4a + 4 = (a + 2)^2$,将$a = 3x + 1$代入得:
$(3x + 1 + 2)^2 = (3x + 3)^2 = [3(x + 1)]^2 = 9(x + 1)^2$
因为$(x + 1)^2$是正整数,所以$9(x + 1)^2$能被$9$整除,即$a^2 + 4a + 4$能被$9$整除。