23. (10分)定义:若两个数$x$,$y$满足$x + y = -1$,则称$x$与$y$具有“友好关系”。
(1)判断方程组$\begin{cases}2x - 3y = 2,\\3x - 2y = 1\end{cases}$的解$x$与$y$是否具有“友好关系”,并说明理由;
(2)若方程组$\begin{cases}ax - by = 11,\\2y - x = -8\end{cases}$的解$x$与$y$具有“友好关系”,请求出方程组的解及$a$,$b$的正整数值。
(1)判断方程组$\begin{cases}2x - 3y = 2,\\3x - 2y = 1\end{cases}$的解$x$与$y$是否具有“友好关系”,并说明理由;
(2)若方程组$\begin{cases}ax - by = 11,\\2y - x = -8\end{cases}$的解$x$与$y$具有“友好关系”,请求出方程组的解及$a$,$b$的正整数值。
答案:23. (1) $x$与$y$具有“友好关系” 理由:记$\begin{cases}2x - 3y = 2①,\\3x - 2y = 1②.\end{cases}$
①,得$x + y = -1$,所以方程组的解$x$与$y$具有“友好关系”。
(2) 根据题意,可知$x + y = -1$.联立$\begin{cases}x + y = -1,\\2y - x = -8,\end{cases}$解得$\begin{cases}x = 2,\\y = -3.\end{cases}$
把$\begin{cases}x = 2,\\y = -3\end{cases}$代入$ax - by = 11$,得$2a + 3b = 11$,则$a,b$的正整数值为$\begin{cases}a = 1,\\b = 3\end{cases}$或$\begin{cases}a = 4,\\b = 1\end{cases}$
①,得$x + y = -1$,所以方程组的解$x$与$y$具有“友好关系”。
(2) 根据题意,可知$x + y = -1$.联立$\begin{cases}x + y = -1,\\2y - x = -8,\end{cases}$解得$\begin{cases}x = 2,\\y = -3.\end{cases}$
把$\begin{cases}x = 2,\\y = -3\end{cases}$代入$ax - by = 11$,得$2a + 3b = 11$,则$a,b$的正整数值为$\begin{cases}a = 1,\\b = 3\end{cases}$或$\begin{cases}a = 4,\\b = 1\end{cases}$
24. (10分)小丽购买学习用品的收据如下表(因污损导致部分数据无法识别):
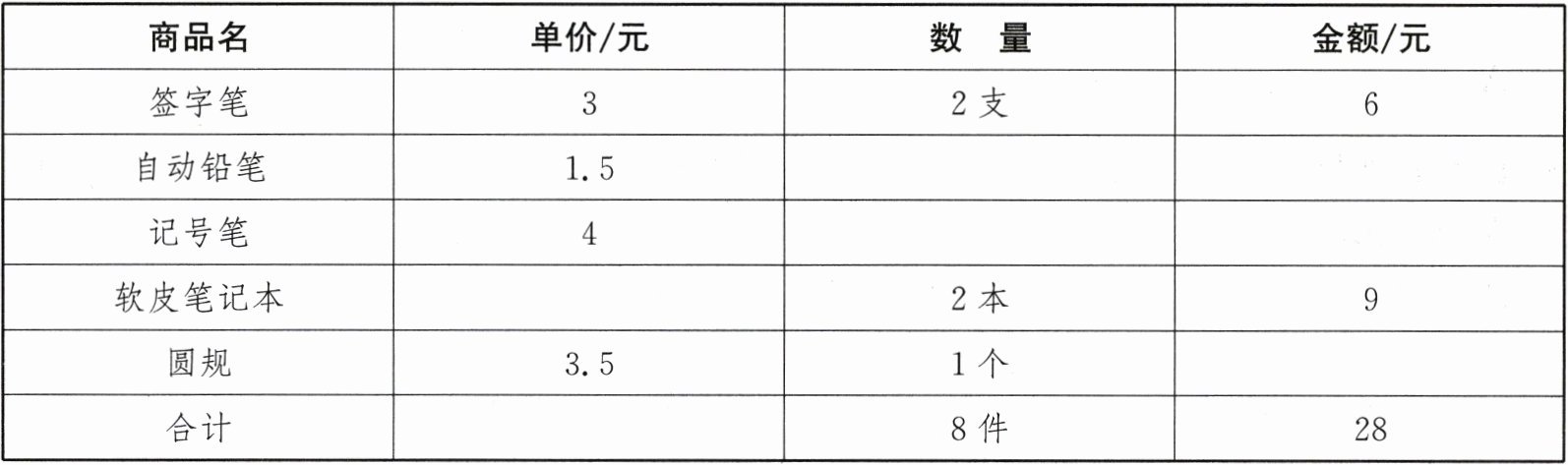
解决下面的问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种学习用品,共花费15元,则有哪几种不同的购买方案?

解决下面的问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种学习用品,共花费15元,则有哪几种不同的购买方案?
答案:24. (1) 设小丽买了自动铅笔$x$支,记号笔$y$支.根据题意,得$\begin{cases}x + y = 8 - (2 + 2 + 1),\\1.5x + 4y = 28 - (6 + 9 + 1 × 3.5),\end{cases}$解得$\begin{cases}x = 1,\\y = 2.\end{cases}$答:小丽买了自动铅笔1支,记号笔2支 (2) 设小丽购买软皮笔记本$m$本,自动铅笔$n$支.根据题意,得$\frac{9}{2}m + 1.5n = 15$,即$3m + n = 10$。因为$m,n$为正整数,所以$\begin{cases}m = 1,\ = 7\end{cases}$或$\begin{cases}m = 2,\ = 4\end{cases}$或$\begin{cases}m = 3,\ = 1\end{cases}$,所以有3种购买方案:①购买软皮笔记本1本,自动铅笔7支;②购买软皮笔记本2本,自动铅笔4支;③购买软皮笔记本3本,自动铅笔1支