9. 对一个概念
作出明确规定
的语句叫作这个概念的定义。答案:9.作出明确规定
10. 写出命题“互为倒数的两个数乘积为1”的逆命题:
乘积为1的两个数互为倒数
。答案:10.乘积为1的两个数互为倒数
11. “若ab > 0,则a > 0,b > 0”的逆命题是
真
命题(选填“真”或“假”)。答案:11.真
12. 如图,在直角三角形ABC中,∠A = 90°,点C与点B关于DE成轴对称,连接BE,∠ABE = 3∠EBD,则∠C的度数是
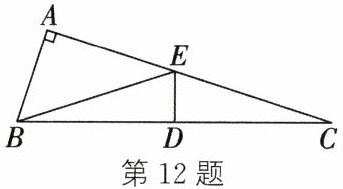
18°
。
答案:12.18°
解析:
解:设∠EBD = x,则∠ABE = 3x。
∵点C与点B关于DE成轴对称,
∴DE垂直平分BC,
∴BE = CE,BD = CD,
∴∠EBD = ∠C = x。
在Rt△ABC中,∠A = 90°,
∴∠ABC + ∠C = 90°,
∵∠ABC = ∠ABE + ∠EBD = 3x + x = 4x,
∴4x + x = 90°,
解得x = 18°,
即∠C = 18°。
18°
∵点C与点B关于DE成轴对称,
∴DE垂直平分BC,
∴BE = CE,BD = CD,
∴∠EBD = ∠C = x。
在Rt△ABC中,∠A = 90°,
∴∠ABC + ∠C = 90°,
∵∠ABC = ∠ABE + ∠EBD = 3x + x = 4x,
∴4x + x = 90°,
解得x = 18°,
即∠C = 18°。
18°
13. 如图所示为第四套人民币中的菊花一角硬币,该硬币边缘镌刻一个正九边形。若直线AC,BC与正九边形的两条边重合,且A,B是同一条边的两个顶点,则∠ACB =

100
°。
答案:13.100
解析:
解:正九边形的内角和为$(9 - 2)×180^{\circ} = 1260^{\circ}$,每个内角为$\frac{1260^{\circ}}{9} = 140^{\circ}$。
设正九边形的中心为$O$,连接$OA$、$OB$、$OC$。正九边形的中心角为$\frac{360^{\circ}}{9} = 40^{\circ}$。
因为$A$、$B$是同一条边的两个顶点,$AC$、$BC$与正九边形的两条边重合,所以$OA$、$OB$、$OC$之间的夹角分别为$40^{\circ}$和$80^{\circ}$(或其他对应角度,具体根据顶点位置,核心是计算圆周角)。
在$\triangle ABC$中,$\angle CAB$和$\angle CBA$分别为正九边形内角的补角的一半(或直接利用圆周角定理),可得$\angle ACB = 180^{\circ} - 2×(180^{\circ} - 140^{\circ}) = 100^{\circ}$。
$100$
设正九边形的中心为$O$,连接$OA$、$OB$、$OC$。正九边形的中心角为$\frac{360^{\circ}}{9} = 40^{\circ}$。
因为$A$、$B$是同一条边的两个顶点,$AC$、$BC$与正九边形的两条边重合,所以$OA$、$OB$、$OC$之间的夹角分别为$40^{\circ}$和$80^{\circ}$(或其他对应角度,具体根据顶点位置,核心是计算圆周角)。
在$\triangle ABC$中,$\angle CAB$和$\angle CBA$分别为正九边形内角的补角的一半(或直接利用圆周角定理),可得$\angle ACB = 180^{\circ} - 2×(180^{\circ} - 140^{\circ}) = 100^{\circ}$。
$100$
14. 用反证法证明“已知:m是正整数,且m²是偶数。求证:m是偶数”时,应先假设
m不是偶数(或m是奇数)
。答案:14.m不是偶数(或m是奇数)
15. 将两张三角形纸片按如图所示的方式摆放,量得∠1 + ∠2 + ∠3 + ∠4 = 220°,则∠5的度数为
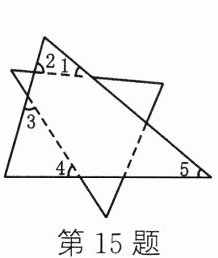
40°
。
答案:15.40°
解析:
解:由三角形内角和定理,两个三角形内角和为$180^{\circ}×2 = 360^{\circ}$。
$\angle1+\angle2+\angle3+\angle4+$(与$\angle5$互补的角)$= 360^{\circ}$,已知$\angle1+\angle2+\angle3+\angle4 = 220^{\circ}$,则与$\angle5$互补的角为$360^{\circ}-220^{\circ}=140^{\circ}$。
$\angle5 = 180^{\circ}-140^{\circ}=40^{\circ}$。
$40^{\circ}$
$\angle1+\angle2+\angle3+\angle4+$(与$\angle5$互补的角)$= 360^{\circ}$,已知$\angle1+\angle2+\angle3+\angle4 = 220^{\circ}$,则与$\angle5$互补的角为$360^{\circ}-220^{\circ}=140^{\circ}$。
$\angle5 = 180^{\circ}-140^{\circ}=40^{\circ}$。
$40^{\circ}$
16. 如图,直线CE//DF,∠CAB = 125°,∠ABD = 85°,则∠1 + ∠2的度数为
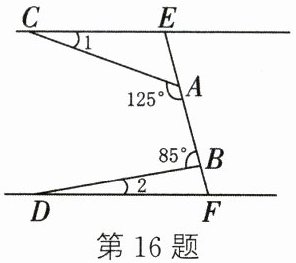
30°
。
答案:16.30°
解析:
解:过点A作AG//CE,过点B作BH//DF。
∵CE//DF,
∴AG//BH//CE//DF。
∴∠1=∠CAG,∠2=∠DBH,∠GAB+∠HBA=180°。
∵∠CAB=∠CAG+∠GAB=125°,∠ABD=∠HBA+∠DBH=85°,
∴∠1+∠2=(∠CAB+∠ABD)-(∠GAB+∠HBA)=125°+85°-180°=30°。
故∠1+∠2的度数为30°。
∵CE//DF,
∴AG//BH//CE//DF。
∴∠1=∠CAG,∠2=∠DBH,∠GAB+∠HBA=180°。
∵∠CAB=∠CAG+∠GAB=125°,∠ABD=∠HBA+∠DBH=85°,
∴∠1+∠2=(∠CAB+∠ABD)-(∠GAB+∠HBA)=125°+85°-180°=30°。
故∠1+∠2的度数为30°。
17. 若一个五边形被截掉一个角后,得到一个多边形,则这个多边形的内角和是
360°或540°或720°
。答案:17.360°或540°或720°
解析:
- 若截线不过任何顶点,多边形边数为$5 + 1=6$,内角和为$(6 - 2)×180°=720°$;
若截线过一个顶点,多边形边数为$5$,内角和为$(5 - 2)×180°=540°$;
若截线过两个顶点,多边形边数为$5 - 1=4$,内角和为$(4 - 2)×180°=360°$。
360°或540°或720°
若截线过一个顶点,多边形边数为$5$,内角和为$(5 - 2)×180°=540°$;
若截线过两个顶点,多边形边数为$5 - 1=4$,内角和为$(4 - 2)×180°=360°$。
360°或540°或720°
18. 如图,点E在正方形纸片ABCD的AB边上,连接CE,DE,将纸片分别沿直线DE,CE翻折,点A,B的对应点A',B'均在∠CED外部。若∠DEB' + ∠A'EC = $\frac{1}{2}$∠CED,设∠CED = α°,则α的值是
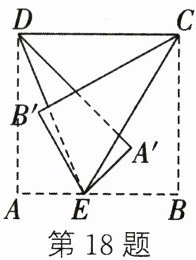
$\frac{360}{7}$
。
答案:18.$\frac{360}{7}$ 解析:根据折叠的性质,可得∠AED=∠A'ED,∠BEC=∠B'EC.
∵∠DEB'=∠B'EC-∠DEC,∠A'EC=∠A'ED-∠DEC,
∴∠DEB'+∠A'EC=∠B'EC+∠A'ED-2∠DEC,即$\frac{1}{2}$α°=∠BEC+∠AED-2α°.整理,得∠BEC+∠AED=$\frac{5}{2}$α°.
∵∠DEA+∠DEC+∠BEC=180°,
∴∠DEA+∠BEC=180°-α°,即180°-α°=$\frac{5}{2}$α°,解得α=$\frac{360}{7}$.
∵∠DEB'=∠B'EC-∠DEC,∠A'EC=∠A'ED-∠DEC,
∴∠DEB'+∠A'EC=∠B'EC+∠A'ED-2∠DEC,即$\frac{1}{2}$α°=∠BEC+∠AED-2α°.整理,得∠BEC+∠AED=$\frac{5}{2}$α°.
∵∠DEA+∠DEC+∠BEC=180°,
∴∠DEA+∠BEC=180°-α°,即180°-α°=$\frac{5}{2}$α°,解得α=$\frac{360}{7}$.
19. (6分)命题:直角三角形的两锐角互余。
(1)将此命题写成“如果…,那么…”的形式:
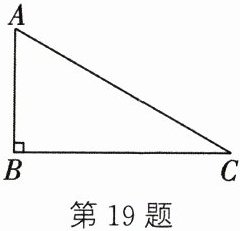
(2)请判断此命题的真假。若为假命题,请说明理由;若为真命题,请根据如图所示的图形写出已知、求证和证明过程。
(1)将此命题写成“如果…,那么…”的形式:
如果一个三角形是直角三角形,那么它的两个锐角互余
。(2)请判断此命题的真假。若为假命题,请说明理由;若为真命题,请根据如图所示的图形写出已知、求证和证明过程。

答案:19.(1)如果一个三角形是直角三角形,那么它的两个锐角互余 (2)此命题是真命题 已知:在△ABC中,∠B=90°.求证:∠A+∠C=90°.证明:
∵∠A+∠B+∠C=180°,
∴∠A+∠C=180°-∠B.
∵∠B=90°,
∴∠A+∠C=180°-90°=90°,
∴直角三角形的两锐角互余
∵∠A+∠B+∠C=180°,
∴∠A+∠C=180°-∠B.
∵∠B=90°,
∴∠A+∠C=180°-90°=90°,
∴直角三角形的两锐角互余