8. 某中学七年级(1)班组织了一次数学、语文、英语竞赛,其中获得数学一等奖的学生有 8 名、二等奖的学生有 16 名;获得语文一等奖的学生有 3 名、二等奖的学生有 13 名;获得英语一等奖的学生有 7 名、二等奖的学生有 21 名。如果只获得一门学科奖项的学生有 50 名,那么三门学科都获奖的学生最多有(
A.3 名或 6 名
B.3 名
C.4 名
D.6 名
D
)A.3 名或 6 名
B.3 名
C.4 名
D.6 名
答案:8.D 解析:假设三门学科都获奖的学生有x名,则(8+16-x)+(3+13-x)+(7+21-x)≥50,解得x≤6.
∴三门学科都获奖的学生最多有6名.
∴三门学科都获奖的学生最多有6名.
9. 中国科学院自主研发的一款机器人可将宽度小于 $100\mu m$ 的柔性微电极植入实验动物的大脑皮层,$1\mu m = 10^{-6}m$,用科学记数法表示 $100\mu m$ 是
1×10⁻⁴
m。答案:9.1×10⁻⁴
解析:
$1×10^{-4}$
10. 一个正多边形的每个内角为 $135^{\circ}$,则这个正多边形的边数为
8
。答案:10.8
解析:
设这个正多边形的边数为$n$。
因为正$n$边形的内角和公式为$(n - 2)×180^{\circ}$,且每个内角为$135^{\circ}$,所以可得方程:
$\frac{(n - 2)×180^{\circ}}{n} = 135^{\circ}$
解方程:
$(n - 2)×180 = 135n$
$180n - 360 = 135n$
$180n - 135n = 360$
$45n = 360$
$n = 8$
8
因为正$n$边形的内角和公式为$(n - 2)×180^{\circ}$,且每个内角为$135^{\circ}$,所以可得方程:
$\frac{(n - 2)×180^{\circ}}{n} = 135^{\circ}$
解方程:
$(n - 2)×180 = 135n$
$180n - 360 = 135n$
$180n - 135n = 360$
$45n = 360$
$n = 8$
8
11. 若 $2^{6} = 4^{a} = b^{2}$,则 $a + b$ 的值为
11或-5
。答案:11.11或-5 解析:
∵2⁶=4ᵃ=b²,
∴4ᵃ=b²=64,
∴a=3,b=±8,
∴a+b=11或-5.
∵2⁶=4ᵃ=b²,
∴4ᵃ=b²=64,
∴a=3,b=±8,
∴a+b=11或-5.
12. 某学校组织学生乘汽车到距离学校 50 千米的植物园春游,早晨 8:00 从学校出发,汽车匀速行驶,计划不能迟于 8:30 到达植物园。设汽车的速度为 $x$ 千米/时,则列一元一次不等式为
$\frac{30}{60}x\geq50$
(不用化简)。答案:12.$\frac{30}{60}x\geq50$
13. 已知命题:任何正数的平方都大于这个数本身,请举一个反例:
答案不唯一,如当正数为$\frac{1}{2}$时,$(\frac{1}{2})^2=$$\frac{1}{4}<\frac{1}{2}$
,说明该命题是假命题。答案:13.答案不唯一,如当正数为$\frac{1}{2}$时,$(\frac{1}{2})^2=$$\frac{1}{4}<\frac{1}{2}$
14. 如图所示为一个运算程序,若需要经过两次运算才能输出结果,则 $x$ 的取值范围是
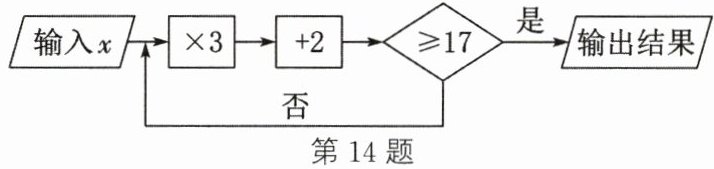
1≤x<5
。
答案:14.1≤x<5
解析:
解:第一次运算结果为$3x + 2$,因为需两次运算,所以第一次运算结果小于17,即$3x + 2 < 17$,解得$x < 5$。
第二次运算将第一次结果代入,即$3(3x + 2) + 2 \geq 17$,化简得$9x + 6 + 2 \geq 17$,$9x \geq 9$,解得$x \geq 1$。
综上,$1 \leq x < 5$。
$1 \leq x < 5$
第二次运算将第一次结果代入,即$3(3x + 2) + 2 \geq 17$,化简得$9x + 6 + 2 \geq 17$,$9x \geq 9$,解得$x \geq 1$。
综上,$1 \leq x < 5$。
$1 \leq x < 5$
15. 有下列两组数,第一组:$-\frac{13}{4}$,$0.3$,$\frac{1}{2}$,$2.25$,$-\frac{3}{10}$;第二组:$\frac{4}{5}$,$-\frac{1}{6}$,$3.2$,$\frac{13}{6}$。将第一组中的每一个数与第二组中的每一个数相乘,则所有乘积的和是
-3
。答案:15.-3
解析:
设第一组数的和为$S_1$,第二组数的和为$S_2$。
$S_1=-\frac{13}{4}+0.3+\frac{1}{2}+2.25-\frac{3}{10}$
$=-\frac{13}{4}+\frac{3}{10}+\frac{1}{2}+\frac{9}{4}-\frac{3}{10}$
$=(-\frac{13}{4}+\frac{9}{4})+(\frac{3}{10}-\frac{3}{10})+\frac{1}{2}$
$=-\frac{4}{4}+0+\frac{1}{2}$
$=-1+\frac{1}{2}=-\frac{1}{2}$
$S_2=\frac{4}{5}-\frac{1}{6}+3.2+\frac{13}{6}$
$=\frac{4}{5}+\frac{16}{5}+(-\frac{1}{6}+\frac{13}{6})$
$=\frac{20}{5}+\frac{12}{6}$
$=4 + 2=6$
所有乘积的和为$S_1× S_2=(-\frac{1}{2})×6=-3$
-3
$S_1=-\frac{13}{4}+0.3+\frac{1}{2}+2.25-\frac{3}{10}$
$=-\frac{13}{4}+\frac{3}{10}+\frac{1}{2}+\frac{9}{4}-\frac{3}{10}$
$=(-\frac{13}{4}+\frac{9}{4})+(\frac{3}{10}-\frac{3}{10})+\frac{1}{2}$
$=-\frac{4}{4}+0+\frac{1}{2}$
$=-1+\frac{1}{2}=-\frac{1}{2}$
$S_2=\frac{4}{5}-\frac{1}{6}+3.2+\frac{13}{6}$
$=\frac{4}{5}+\frac{16}{5}+(-\frac{1}{6}+\frac{13}{6})$
$=\frac{20}{5}+\frac{12}{6}$
$=4 + 2=6$
所有乘积的和为$S_1× S_2=(-\frac{1}{2})×6=-3$
-3
16. 若关于 $x$ 的不等式组 $\begin{cases}\frac{2x + 1}{2} + 3 > -1,\\x < m\end{cases}$ 的所有整数解的和是 $-9$,则 $m$ 的取值范围是 ______ 。
答案:16.-2<m≤-1或1<m≤2 解析:
∵原不等式组有解,
∴原不等式组的解集为$-\frac{9}{2}<x<m$.
∵不等式组的所有整数解的和是-9,
∴整数解是x=-4,-3,-2或x=-4,-3,-2,-1,0,1,
∴m的取值范围是-2<m≤-1或1<m≤2.
∵原不等式组有解,
∴原不等式组的解集为$-\frac{9}{2}<x<m$.
∵不等式组的所有整数解的和是-9,
∴整数解是x=-4,-3,-2或x=-4,-3,-2,-1,0,1,
∴m的取值范围是-2<m≤-1或1<m≤2.
17. 如图,$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F + \angle G = $_________$^{\circ}$。
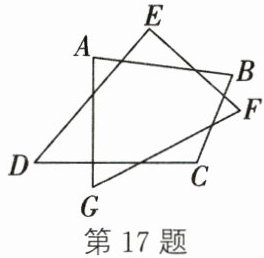

答案:
17.540 解析:如图,连接AE,BD,记AB与DE的交点为O,在四边形AGFE中,∠GAB+∠1+∠2+∠DEF+∠G+∠F=360°,在△BDC中,∠5+∠6+∠C=180°.
∵∠1+∠2+∠AOE=∠3+∠4+∠BOD,∠AOE=∠BOD,
∴∠1+∠2=∠3+∠4.
∵∠EDC=∠3+∠5,∠ABC=∠4+∠6,
∴∠GAB+∠ABC+∠C+∠EDC+∠DEF+∠F+∠G=∠GAB+∠4+∠6+∠C+∠3+∠5+∠DEF+∠F+∠G=∠GAB+∠3+∠4+∠DEF+∠G+∠F+∠5+∠6+∠C=(∠GAB+∠1+∠2+∠DEF+∠G+∠F)+(∠5+∠6+∠C)=360°+180°=540°.
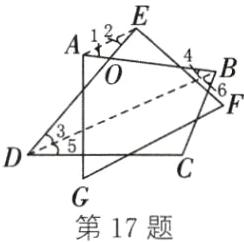
17.540 解析:如图,连接AE,BD,记AB与DE的交点为O,在四边形AGFE中,∠GAB+∠1+∠2+∠DEF+∠G+∠F=360°,在△BDC中,∠5+∠6+∠C=180°.
∵∠1+∠2+∠AOE=∠3+∠4+∠BOD,∠AOE=∠BOD,
∴∠1+∠2=∠3+∠4.
∵∠EDC=∠3+∠5,∠ABC=∠4+∠6,
∴∠GAB+∠ABC+∠C+∠EDC+∠DEF+∠F+∠G=∠GAB+∠4+∠6+∠C+∠3+∠5+∠DEF+∠F+∠G=∠GAB+∠3+∠4+∠DEF+∠G+∠F+∠5+∠6+∠C=(∠GAB+∠1+∠2+∠DEF+∠G+∠F)+(∠5+∠6+∠C)=360°+180°=540°.

18. 如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$AB = 13$,$AC = 12$,$BC = 5$,将 $\triangle ABC$ 绕点 $C$ 顺时针旋转,点 $A$,$B$ 的对应点分别是 $A'$,$B'$,$D$ 为线段 $AC$ 上一点,且 $CD = 4$,$E$ 为线段 $A'B'$ 上一动点。在旋转过程中,线段 $ED$ 长的取值范围是
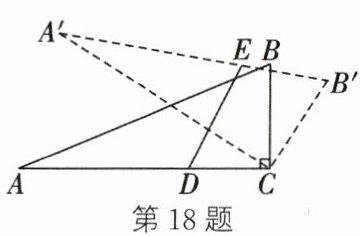
$\frac{8}{13} \leq ED\leq16$
。
答案:
18.$\frac{8}{13} \leq ED\leq16$ 解析:如图①,连接CE.
∵DE≥CE-CD,
∴当CE⊥A′B′,且点D在CE上时,DE的长最小(如图②).由旋转,可得BC=B′C=5,AC=A′C=12,AB=A′B′=13,∠ACB=∠A′CB′=90°.
∵$2S_{\triangle A'B'C}=A'C· B'C=A'B'· CE$,
∴$CE=\frac{A'C· B'C}{A'B'}=\frac{12×5}{13}=\frac{60}{13}$,
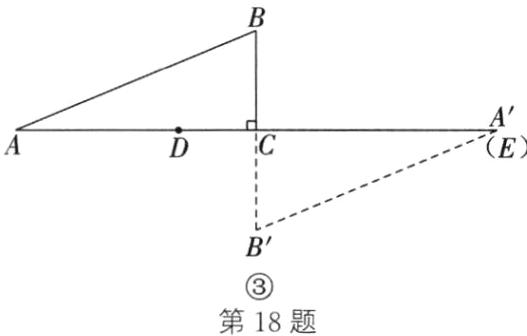
∴DE=CE-CD=$\frac{60}{13}-4=\frac{8}{13}$,即DE长的最小值为$\frac{8}{13}$.当点E与点A′重合,且点D在EC的延长线上时,DE的长最大(如图③).此时DE=CD+A′C=4+12=16.
∴线段ED长的取值范围是$\frac{8}{13} \leq ED\leq16$.


18.$\frac{8}{13} \leq ED\leq16$ 解析:如图①,连接CE.
∵DE≥CE-CD,
∴当CE⊥A′B′,且点D在CE上时,DE的长最小(如图②).由旋转,可得BC=B′C=5,AC=A′C=12,AB=A′B′=13,∠ACB=∠A′CB′=90°.
∵$2S_{\triangle A'B'C}=A'C· B'C=A'B'· CE$,
∴$CE=\frac{A'C· B'C}{A'B'}=\frac{12×5}{13}=\frac{60}{13}$,
∴DE=CE-CD=$\frac{60}{13}-4=\frac{8}{13}$,即DE长的最小值为$\frac{8}{13}$.当点E与点A′重合,且点D在EC的延长线上时,DE的长最大(如图③).此时DE=CD+A′C=4+12=16.
∴线段ED长的取值范围是$\frac{8}{13} \leq ED\leq16$.


