1. 若(
A.$a$
B.$2a$
C.$ab$
D.$2ab$
A
)·$2a^{2}b = 2a^{3}b$,则括号内应填的单项式为(A
)A.$a$
B.$2a$
C.$ab$
D.$2ab$
答案:1.A
解析:
设括号内的单项式为$x$,则$x · 2a^{2}b = 2a^{3}b$,解得$x = \frac{2a^{3}b}{2a^{2}b} = a$,答案选A。
2. 下列运算中,正确的是(
A.$a(a + 1) = a^{2} + 1$
B.$a(a - 1) = a^{2} - a$
C.$(a + 1)(a - 1) = a^{2} + 1$
D.$(a + 1)^{2} = a^{2} + 1$
B
)A.$a(a + 1) = a^{2} + 1$
B.$a(a - 1) = a^{2} - a$
C.$(a + 1)(a - 1) = a^{2} + 1$
D.$(a + 1)^{2} = a^{2} + 1$
答案:2.B
3. 若$(x + 3y)^{2} = (x - 3y)^{2} + M$,则$M$等于(
A.$6xy$
B.$12xy$
C.$-6xy$
D.$-12xy$
B
)A.$6xy$
B.$12xy$
C.$-6xy$
D.$-12xy$
答案:3.B
解析:
$(x + 3y)^{2} = x^{2} + 6xy + 9y^{2}$,$(x - 3y)^{2} = x^{2} - 6xy + 9y^{2}$,由$(x + 3y)^{2} = (x - 3y)^{2} + M$,得$x^{2} + 6xy + 9y^{2} = x^{2} - 6xy + 9y^{2} + M$,移项可得$M = x^{2} + 6xy + 9y^{2} - x^{2} + 6xy - 9y^{2} = 12xy$。
B
B
4. 下列算式中,能用平方差公式计算的是(
A.$(m + 2n)(2m - n)$
B.$(m + n)(m - n)$
C.$(m + n)(-m - n)$
D.$(-m + n)(n - m)$
B
)A.$(m + 2n)(2m - n)$
B.$(m + n)(m - n)$
C.$(m + n)(-m - n)$
D.$(-m + n)(n - m)$
答案:4.B
5. 方程$x(x - 1) - 2(x + 1) = x(x - 2)$的解为(
A.$x = 1$
B.$x = -1$
C.$x = -2$
D.$x = 2$
C
)A.$x = 1$
B.$x = -1$
C.$x = -2$
D.$x = 2$
答案:5.C
解析:
解:去括号,得$x^{2}-x - 2x - 2 = x^{2}-2x$,
移项、合并同类项,得$-x - 2 = 0$,
解得$x = -2$。
C
移项、合并同类项,得$-x - 2 = 0$,
解得$x = -2$。
C
6. 若$M = (a + 3)(a - 4)$,$N = (a + 2)(2a - 5)$,其中$a$为有理数,则$M$,$N$的大小关系为(
A.$M > N$
B.$M < N$
C.$M = N$
D.无法确定
B
)A.$M > N$
B.$M < N$
C.$M = N$
D.无法确定
答案:6.B
解析:
$M=(a+3)(a-4)=a^2 - a - 12$,$N=(a+2)(2a - 5)=2a^2 - a - 10$,$N - M=(2a^2 - a - 10)-(a^2 - a - 12)=a^2 + 2$,因为$a^2\geq0$,所以$a^2 + 2\geq2>0$,即$N - M>0$,所以$M<N$。
B
B
7. 如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”。下列数中,属于“幸福数”的是(
A.205
B.250
C.502
D.520
D
)A.205
B.250
C.502
D.520
答案:7.D 解析:设较小的奇数为x,则较大的奇数为x + 2。根据题意,得(x + 2)² - x² = x² + 4x + 4 - x² = 4x + 4。若4x + 4 = 205,则x = $\frac{201}{4}$,不是整数,不符合题意;若4x + 4 = 250,则x = $\frac{123}{2}$,不是整数,不符合题意;若4x + 4 = 502,则x = $\frac{249}{2}$,不是整数,不符合题意;若4x + 4 = 520,则x = 129,符合题意。
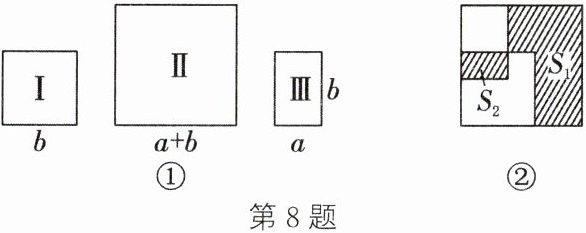
8. 如图①,Ⅰ是边长为$b$的正方形纸片,Ⅱ是边长为$a + b$的正方形纸片,Ⅲ是长为$b$、宽为$a$的长方形纸片$(b > a)$,将Ⅰ,Ⅲ按如图②所示的方式放入纸片Ⅱ内。若图②中两块阴影部分的面积分别为$S_{1}$和$S_{2}$,则要求$S_{1} - 2S_{2}$的值,只需要知道(
A.$a$的值
B.$b$的值
C.$a^{2} + b^{2}$的值
D.$a^{2} - b^{2}$的值
A
)
A.$a$的值
B.$b$的值
C.$a^{2} + b^{2}$的值
D.$a^{2} - b^{2}$的值
答案:8.A 解析:由题图,可知S₁ = S₁₁ - (S₁ + S₃ - S₂),S₂ = a[2b - (a + b)] = ab - a²,S₁₁ = (a + b)² = a² + b² + 2ab,S₁ = b²,S₃ = ab,即S₁ = a² + b² + 2ab - (b² + ab - ab + a²) = 2ab,所以S₁ - 2S₂ = 2ab - 2(ab - a²) = 2a²,故只需要知道a的值。
9. 计算:$3a^{3}·(-4a^{2}) =$
-12a⁵
。答案:9. -12a⁵
解析:
$-12a^{5}$
10. 计算$a(a + 1) - a$的结果是
a²
。答案:10.a²
解析:
$a(a + 1) - a$
$=a^2 + a - a$
$=a^2$
$=a^2 + a - a$
$=a^2$
11. 若$(1 + x)(2x^{2} + ax + 1)$的计算结果中$x^{2}$项的系数为$-2$,则$a$的值为
-4
。答案:11. -4
解析:
解:$(1 + x)(2x^{2} + ax + 1)$
$=1×(2x^{2} + ax + 1)+x×(2x^{2} + ax + 1)$
$=2x^{2} + ax + 1 + 2x^{3} + ax^{2} + x$
$=2x^{3}+(2 + a)x^{2}+(a + 1)x + 1$
因为$x^{2}$项的系数为$-2$,所以$2 + a=-2$,解得$a=-4$。
-4
$=1×(2x^{2} + ax + 1)+x×(2x^{2} + ax + 1)$
$=2x^{2} + ax + 1 + 2x^{3} + ax^{2} + x$
$=2x^{3}+(2 + a)x^{2}+(a + 1)x + 1$
因为$x^{2}$项的系数为$-2$,所以$2 + a=-2$,解得$a=-4$。
-4
12. 已知代数式$a^{2} + (2t - 1)ab + 4b^{2}$是一个完全平方式,则常数$t$的值为
$\frac{5}{2}$或 - $\frac{3}{2}$
。答案:12. $\frac{5}{2}$或 - $\frac{3}{2}$
解析:
解:因为代数式$a^{2} + (2t - 1)ab + 4b^{2}$是完全平方式,所以$(2t - 1)ab = \pm 2 · a · 2b$。
当$(2t - 1)ab = 2 · a · 2b$时,$2t - 1 = 4$,解得$t = \frac{5}{2}$;
当$(2t - 1)ab = -2 · a · 2b$时,$2t - 1 = -4$,解得$t = -\frac{3}{2}$。
综上,$t$的值为$\frac{5}{2}$或$-\frac{3}{2}$。
当$(2t - 1)ab = 2 · a · 2b$时,$2t - 1 = 4$,解得$t = \frac{5}{2}$;
当$(2t - 1)ab = -2 · a · 2b$时,$2t - 1 = -4$,解得$t = -\frac{3}{2}$。
综上,$t$的值为$\frac{5}{2}$或$-\frac{3}{2}$。
13. 在长为$3a + 2$、宽为$2a + 3$的长方形铁皮上,剪去一个边长为$a - 1(a > 1)$的小正方形,则剩余部分的面积为
5a² + 15a + 5
。答案:13.5a² + 15a + 5
解析:
长方形面积为$(3a + 2)(2a + 3)$,小正方形面积为$(a - 1)^2$。
$\begin{aligned}&(3a + 2)(2a + 3)-(a - 1)^2\\=&6a^2 + 9a + 4a + 6-(a^2 - 2a + 1)\\=&6a^2 + 13a + 6 - a^2 + 2a - 1\\=&5a^2 + 15a + 5\end{aligned}$
$5a^2 + 15a + 5$
$\begin{aligned}&(3a + 2)(2a + 3)-(a - 1)^2\\=&6a^2 + 9a + 4a + 6-(a^2 - 2a + 1)\\=&6a^2 + 13a + 6 - a^2 + 2a - 1\\=&5a^2 + 15a + 5\end{aligned}$
$5a^2 + 15a + 5$