14. 若$(x - 3)^{2} + (x - 7)^{2} = 30$,则$(x - 5)^{2}$的值为
11
。答案:14.11
解析:
设$t = x - 5$,则$x = t + 5$。
将$x = t + 5$代入$(x - 3)^2 + (x - 7)^2 = 30$,得:
$\begin{aligned}(t + 5 - 3)^2 + (t + 5 - 7)^2 &= 30\\(t + 2)^2 + (t - 2)^2 &= 30\\(t^2 + 4t + 4) + (t^2 - 4t + 4) &= 30\\2t^2 + 8 &= 30\\2t^2 &= 22\\t^2 &= 11\end{aligned}$
因为$t = x - 5$,所以$(x - 5)^2 = t^2 = 11$。
11
将$x = t + 5$代入$(x - 3)^2 + (x - 7)^2 = 30$,得:
$\begin{aligned}(t + 5 - 3)^2 + (t + 5 - 7)^2 &= 30\\(t + 2)^2 + (t - 2)^2 &= 30\\(t^2 + 4t + 4) + (t^2 - 4t + 4) &= 30\\2t^2 + 8 &= 30\\2t^2 &= 22\\t^2 &= 11\end{aligned}$
因为$t = x - 5$,所以$(x - 5)^2 = t^2 = 11$。
11
15. 已知$x = 2^{m} + 1$,$y = 3 + 2^{m + 1}$。若用含$x$的代数式表示$y$,则$y =$
2x + 1
。答案:15.2x + 1
解析:
由$x = 2^{m} + 1$,得$2^{m}=x - 1$。
$y = 3 + 2^{m + 1}=3 + 2×2^{m}$,将$2^{m}=x - 1$代入,得$y = 3 + 2(x - 1)=2x + 1$。
$y = 2x + 1$
$y = 3 + 2^{m + 1}=3 + 2×2^{m}$,将$2^{m}=x - 1$代入,得$y = 3 + 2(x - 1)=2x + 1$。
$y = 2x + 1$
16. 如果$2x^{2} + 2xy + y^{2} - 2x + 1 = 0$,那么$xy$的值为
-1
。答案:16. -1
解析:
$2x^{2} + 2xy + y^{2} - 2x + 1 = 0$,
将原式变形为:$(x^{2} + 2xy + y^{2}) + (x^{2} - 2x + 1) = 0$,
即$(x + y)^{2} + (x - 1)^{2} = 0$,
因为$(x + y)^{2} \geq 0$,$(x - 1)^{2} \geq 0$,
所以$x + y = 0$且$x - 1 = 0$,
解得$x = 1$,$y = -1$,
则$xy = 1×(-1) = -1$。
-1
将原式变形为:$(x^{2} + 2xy + y^{2}) + (x^{2} - 2x + 1) = 0$,
即$(x + y)^{2} + (x - 1)^{2} = 0$,
因为$(x + y)^{2} \geq 0$,$(x - 1)^{2} \geq 0$,
所以$x + y = 0$且$x - 1 = 0$,
解得$x = 1$,$y = -1$,
则$xy = 1×(-1) = -1$。
-1
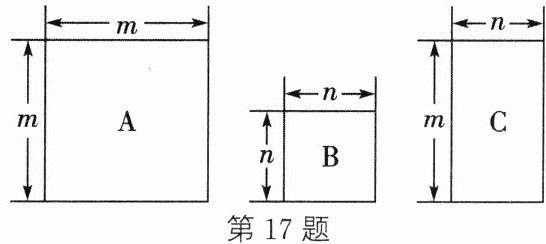
17. 现有如图所示的A,B,C三种纸片若干张。淇淇要用这三种纸片紧密拼接成一个没有缝隙的大正方形,她选取A纸片9张,再取B纸片1张,还需要取C纸片
6
张。
答案:17.6
解析:
设大正方形的边长为 $a$。
A纸片是边长为 $m$ 的正方形,面积为 $m^2$,9张A纸片面积为 $9m^2$;B纸片是边长为 $n$ 的正方形,面积为 $n^2$,1张B纸片面积为 $n^2$;C纸片是长为 $m$、宽为 $n$ 的长方形,面积为 $mn$,设需 $k$ 张C纸片,面积为 $kmn$。
大正方形面积为 $a^2 = 9m^2 + n^2 + kmn$。
因为是正方形,可设 $a = 3m + n$(或其他组合,经检验此组合合理),则 $a^2=(3m + n)^2 = 9m^2 + 6mn + n^2$。
对比可得 $k = 6$。
6
A纸片是边长为 $m$ 的正方形,面积为 $m^2$,9张A纸片面积为 $9m^2$;B纸片是边长为 $n$ 的正方形,面积为 $n^2$,1张B纸片面积为 $n^2$;C纸片是长为 $m$、宽为 $n$ 的长方形,面积为 $mn$,设需 $k$ 张C纸片,面积为 $kmn$。
大正方形面积为 $a^2 = 9m^2 + n^2 + kmn$。
因为是正方形,可设 $a = 3m + n$(或其他组合,经检验此组合合理),则 $a^2=(3m + n)^2 = 9m^2 + 6mn + n^2$。
对比可得 $k = 6$。
6
18. 如图①,我国南宋数学家杨辉在其著作《详解九章算法》中揭示了$(a + b)^{n}$($n$为非负整数)展开式的项数及各项系数的有关规律。后人也将图②称为“杨辉三角”,则$(a + b)^{7}$的展开式中所有项的系数和是
128
。答案:18.128 解析:当n = 0时,展开式中所有项的系数和为1 = 2⁰,当n = 1时,展开式中所有项的系数和为2 = 2¹;当n = 2时,展开式中所有项的系数和为4 = 2²……当n = 7时,展开式中所有项的系数和为2⁷ = 128。
19. (12分)计算:
(1)$(x - y)(x - 3y) - 2x(x - 2y)$;
(2)$(x + 2y)(x - 2y) - (x - 3y)^{2}$;
(3)$(3a + b - 2)(3a - b + 2)$;
(4)$(y^{2} - 9x^{2})[(3x - y)^{2} + (3x + y)^{2}]$。
(1)$(x - y)(x - 3y) - 2x(x - 2y)$;
(2)$(x + 2y)(x - 2y) - (x - 3y)^{2}$;
(3)$(3a + b - 2)(3a - b + 2)$;
(4)$(y^{2} - 9x^{2})[(3x - y)^{2} + (3x + y)^{2}]$。
答案:19.(1) -x² + 3y² (2) -13y² + 6xy (3)9a² - b² + 4b - 4 (4)2y⁴ - 162x⁴
解析:
(1)$(x - y)(x - 3y) - 2x(x - 2y)$
$=x^{2}-3xy-xy+3y^{2}-2x^{2}+4xy$
$=-x^{2}+3y^{2}$
(2)$(x + 2y)(x - 2y) - (x - 3y)^{2}$
$=x^{2}-4y^{2}-(x^{2}-6xy+9y^{2})$
$=x^{2}-4y^{2}-x^{2}+6xy-9y^{2}$
$=-13y^{2}+6xy$
(3)$(3a + b - 2)(3a - b + 2)$
$=[3a+(b-2)][3a-(b-2)]$
$=(3a)^{2}-(b-2)^{2}$
$=9a^{2}-(b^{2}-4b+4)$
$=9a^{2}-b^{2}+4b-4$
(4)$(y^{2} - 9x^{2})[(3x - y)^{2} + (3x + y)^{2}]$
$=(y^{2}-9x^{2})[(9x^{2}-6xy+y^{2})+(9x^{2}+6xy+y^{2})]$
$=(y^{2}-9x^{2})(18x^{2}+2y^{2})$
$=y^{2}·18x^{2}+y^{2}·2y^{2}-9x^{2}·18x^{2}-9x^{2}·2y^{2}$
$=18x^{2}y^{2}+2y^{4}-162x^{4}-18x^{2}y^{2}$
$=2y^{4}-162x^{4}$
$=x^{2}-3xy-xy+3y^{2}-2x^{2}+4xy$
$=-x^{2}+3y^{2}$
(2)$(x + 2y)(x - 2y) - (x - 3y)^{2}$
$=x^{2}-4y^{2}-(x^{2}-6xy+9y^{2})$
$=x^{2}-4y^{2}-x^{2}+6xy-9y^{2}$
$=-13y^{2}+6xy$
(3)$(3a + b - 2)(3a - b + 2)$
$=[3a+(b-2)][3a-(b-2)]$
$=(3a)^{2}-(b-2)^{2}$
$=9a^{2}-(b^{2}-4b+4)$
$=9a^{2}-b^{2}+4b-4$
(4)$(y^{2} - 9x^{2})[(3x - y)^{2} + (3x + y)^{2}]$
$=(y^{2}-9x^{2})[(9x^{2}-6xy+y^{2})+(9x^{2}+6xy+y^{2})]$
$=(y^{2}-9x^{2})(18x^{2}+2y^{2})$
$=y^{2}·18x^{2}+y^{2}·2y^{2}-9x^{2}·18x^{2}-9x^{2}·2y^{2}$
$=18x^{2}y^{2}+2y^{4}-162x^{4}-18x^{2}y^{2}$
$=2y^{4}-162x^{4}$
20. (6分)已知$a^{2} - a - 3 = 0$,求代数式$(a - 2)^{2} + (a - 1)(a + 3)$的值。
答案:20.原式 = a² - 4a + 4 + a² + 3a - a - 3 = 2a² - 2a + 1。因为a² - a - 3 = 0,所以a² - a = 3,所以2a² - 2a = 6,所以原式 = 6 + 1 = 7
解析:
解:$(a - 2)^{2} + (a - 1)(a + 3)$
$=a^{2}-4a + 4 + a^{2}+3a - a - 3$
$=2a^{2}-2a + 1$
因为$a^{2}-a - 3 = 0$,所以$a^{2}-a = 3$,则$2a^{2}-2a = 6$,所以原式$=6 + 1 = 7$。
$=a^{2}-4a + 4 + a^{2}+3a - a - 3$
$=2a^{2}-2a + 1$
因为$a^{2}-a - 3 = 0$,所以$a^{2}-a = 3$,则$2a^{2}-2a = 6$,所以原式$=6 + 1 = 7$。