新知梳理
1. 旋转的基本性质:旋转前后的两个图形中,对应点到旋转中心的距离
2. 将一条线段绕其一个端点旋转60°,连接对应点可以得到的图形是
1. 旋转的基本性质:旋转前后的两个图形中,对应点到旋转中心的距离
相等
,对应点与旋转中心连线所成的角都等于旋转角
.2. 将一条线段绕其一个端点旋转60°,连接对应点可以得到的图形是
等边三角形
;将一条线段绕其一个端点旋转90°,连接对应点可以得到的图形是等腰直角三角形
.答案:1.相等 旋转角 2.等边三角形 等腰直角三角形
1. 下列正方形网格中的△ABC绕点O逆时针旋转90°后的图案应该是(

A
)
答案:1.A
2. 如图,将△ABC绕点O顺时针旋转80°得到△DEF,则下列说法不一定正确的是(

A.AB=DE
B.∠CAB=∠FDE
C.∠AOD=80°
D.AB//DF
D
)
A.AB=DE
B.∠CAB=∠FDE
C.∠AOD=80°
D.AB//DF
答案:2.D
解析:
证明:
∵△ABC绕点O顺时针旋转80°得到△DEF,
∴△ABC≌△DEF,旋转角为80°。
A.
∵全等三角形对应边相等,
∴AB=DE,正确;
B.
∵全等三角形对应角相等,
∴∠CAB=∠FDE,正确;
C.
∵旋转角为80°,点A与点D为对应点,
∴∠AOD=80°,正确;
D. 旋转后AB与DF的位置关系不确定,不一定平行,错误。
答案:D
∵△ABC绕点O顺时针旋转80°得到△DEF,
∴△ABC≌△DEF,旋转角为80°。
A.
∵全等三角形对应边相等,
∴AB=DE,正确;
B.
∵全等三角形对应角相等,
∴∠CAB=∠FDE,正确;
C.
∵旋转角为80°,点A与点D为对应点,
∴∠AOD=80°,正确;
D. 旋转后AB与DF的位置关系不确定,不一定平行,错误。
答案:D
3. 如图,将△ABC绕点A逆时针旋转得到△ADE,点B的对应点D恰好落在BC边上.若DE⊥AC,∠CAD=25°,则∠B的度数为
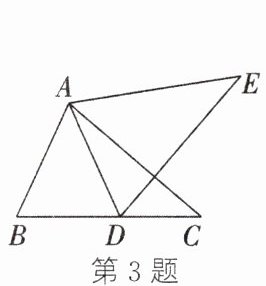
65°
.
答案:3.65°
解析:
证明:
∵△ABC绕点A逆时针旋转得到△ADE,
∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,
∵∠CAD=25°,
∴∠BAC=∠BAD+25°,∠DAE=∠CAE+25°,
∴∠BAD=∠CAE,
∵DE⊥AC,
∴∠AED=90°-∠CAE,
∵∠AED=∠ACB,
∴∠ACB=90°-∠CAE=90°-∠BAD,
∵AB=AD,
∴∠B=∠ADB,
∵∠ADB=∠CAD+∠ACB=25°+∠ACB,
∴∠B=25°+∠ACB,
∵∠B+∠BAC+∠ACB=180°,
∴∠B+(∠BAD+25°)+∠ACB=180°,
∴∠B+∠ACB+∠BAD+25°=180°,
∵∠B=25°+∠ACB,∠ACB=90°-∠BAD,
∴∠B=25°+90°-∠BAD=115°-∠BAD,
∴∠B+(90°-∠BAD)+∠BAD+25°=180°,
∴∠B+115°=180°,
∴∠B=65°.
故答案为:65°
∵△ABC绕点A逆时针旋转得到△ADE,
∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,
∵∠CAD=25°,
∴∠BAC=∠BAD+25°,∠DAE=∠CAE+25°,
∴∠BAD=∠CAE,
∵DE⊥AC,
∴∠AED=90°-∠CAE,
∵∠AED=∠ACB,
∴∠ACB=90°-∠CAE=90°-∠BAD,
∵AB=AD,
∴∠B=∠ADB,
∵∠ADB=∠CAD+∠ACB=25°+∠ACB,
∴∠B=25°+∠ACB,
∵∠B+∠BAC+∠ACB=180°,
∴∠B+(∠BAD+25°)+∠ACB=180°,
∴∠B+∠ACB+∠BAD+25°=180°,
∵∠B=25°+∠ACB,∠ACB=90°-∠BAD,
∴∠B=25°+90°-∠BAD=115°-∠BAD,
∴∠B+(90°-∠BAD)+∠BAD+25°=180°,
∴∠B+115°=180°,
∴∠B=65°.
故答案为:65°
4. 如图,△ABC是等腰直角三角形,∠BCA=90°,D是AB边上一点,△BCD逆时针旋转后到达△ACE的位置.
(1)图中相等的线段有
(2)图中相等的锐角是
(3)如果M是BC的中点,那么经过上述旋转,点M到达的位置是
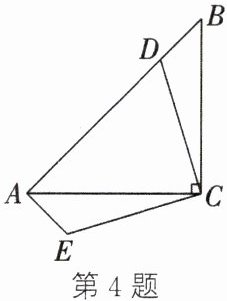
(1)图中相等的线段有
3
组;(2)图中相等的锐角是
∠B=∠BAC=∠CAE,∠BCD=∠ACE
;(3)如果M是BC的中点,那么经过上述旋转,点M到达的位置是
AC的中点处
.
答案:4.(1)3 (2)∠B=∠BAC=∠CAE,∠BCD=∠ACE (3)AC的中点处
解析:
(1)3
(2)$\angle B=\angle BAC=\angle CAE$,$\angle BCD=\angle ACE$
(3)$AC$的中点处
(2)$\angle B=\angle BAC=\angle CAE$,$\angle BCD=\angle ACE$
(3)$AC$的中点处
5. 如图,在正方形ABCD中,E为BC边上的一点,将△ABE顺时针旋转后得到△CBF.
(1)指出旋转中心及旋转角的度数;
(2)判断AE与CF的位置关系,并说明理由;
(3)若正方形ABCD的面积为18cm²,△BCF的面积为5cm²,求四边形AECD的面积.
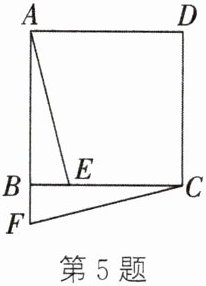
(1)指出旋转中心及旋转角的度数;
(2)判断AE与CF的位置关系,并说明理由;
(3)若正方形ABCD的面积为18cm²,△BCF的面积为5cm²,求四边形AECD的面积.

答案:
5.(1)旋转中心是点B,旋转角的度数是90° (2)AE⊥CF 理由:如图,延长AE交CF于点M.因为将△ABE顺时针旋转后得到△CBF,所以∠EAB=∠FCB.因为∠ABC=90°,所以∠BAE + ∠AEB=90°.又因为∠AEB=∠CEM,所以∠ECM+∠CEM=90°,所以∠CMA=90°,所以AE⊥CF.
(3)因为将△ABE顺时针旋转后得到△CBF,△BCF的面积为5cm²,所以△ABE的面积是5cm².又因为正方形ABCD的面积是18cm²,所以四边形AECD的面积是18 - 5 = 13(cm²)
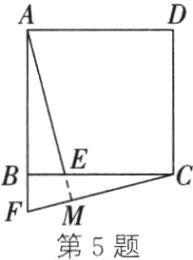
5.(1)旋转中心是点B,旋转角的度数是90° (2)AE⊥CF 理由:如图,延长AE交CF于点M.因为将△ABE顺时针旋转后得到△CBF,所以∠EAB=∠FCB.因为∠ABC=90°,所以∠BAE + ∠AEB=90°.又因为∠AEB=∠CEM,所以∠ECM+∠CEM=90°,所以∠CMA=90°,所以AE⊥CF.
(3)因为将△ABE顺时针旋转后得到△CBF,△BCF的面积为5cm²,所以△ABE的面积是5cm².又因为正方形ABCD的面积是18cm²,所以四边形AECD的面积是18 - 5 = 13(cm²)
