1. (2025·常熟期中)若$x^{3}· x^{m}y^{2n}=x^{9}y^{8}$,则$m + n$的值为(
A.6
B.7
C.9
D.10
D
)A.6
B.7
C.9
D.10
答案:1. D
解析:
因为$x^{3}· x^{m}y^{2n}=x^{3+m}y^{2n}$,又因为$x^{3}· x^{m}y^{2n}=x^{9}y^{8}$,所以$3 + m = 9$,$2n = 8$。解得$m = 6$,$n = 4$。则$m + n = 6 + 4 = 10$。
D
D
2. (2024·成都)下列计算正确的是(
A.$(3x)^{2}=3x^{2}$
B.$3x + 3y = 6xy$
C.$(x + y)^{2}=x^{2}+y^{2}$
D.$(x + 2)(x - 2)=x^{2}-4$
D
)A.$(3x)^{2}=3x^{2}$
B.$3x + 3y = 6xy$
C.$(x + y)^{2}=x^{2}+y^{2}$
D.$(x + 2)(x - 2)=x^{2}-4$
答案:2. D
3. (2024·金坛区期末)已知$2(x + 3)(x - 1)=2x^{2}+mx + n$,则$m - n$的值是(
A.$-10$
B.10
C.$-2$
D.2
B
)A.$-10$
B.10
C.$-2$
D.2
答案:3. B
解析:
$2(x + 3)(x - 1)$
$=2(x^{2}-x + 3x - 3)$
$=2(x^{2}+2x - 3)$
$=2x^{2}+4x - 6$
因为$2(x + 3)(x - 1)=2x^{2}+mx + n$,所以$m = 4$,$n=-6$。
$m - n=4 - (-6)=10$
B
$=2(x^{2}-x + 3x - 3)$
$=2(x^{2}+2x - 3)$
$=2x^{2}+4x - 6$
因为$2(x + 3)(x - 1)=2x^{2}+mx + n$,所以$m = 4$,$n=-6$。
$m - n=4 - (-6)=10$
B
4. (2024·锡山区期中)若$(x - m - 1)$与$(x + \frac{1}{2})$的积不含常数项,则$m =$(
A.$-1$
B.1
C.$-2$
D.2
A
)A.$-1$
B.1
C.$-2$
D.2
答案:4. A
解析:
$(x - m - 1)(x + \frac{1}{2})$
$=x^2 + \frac{1}{2}x - (m + 1)x - \frac{1}{2}(m + 1)$
$=x^2 + [\frac{1}{2} - (m + 1)]x - \frac{1}{2}(m + 1)$
因为积不含常数项,所以$-\frac{1}{2}(m + 1) = 0$
解得$m = -1$
A
$=x^2 + \frac{1}{2}x - (m + 1)x - \frac{1}{2}(m + 1)$
$=x^2 + [\frac{1}{2} - (m + 1)]x - \frac{1}{2}(m + 1)$
因为积不含常数项,所以$-\frac{1}{2}(m + 1) = 0$
解得$m = -1$
A
5. (2024·新北区期中)$(2 + 1)(2^{2}+1)(2^{4}+1)(2^{8}+1)(2^{16}+1)+1$的计算结果中个位数字是(
A.8
B.6
C.4
D.2
B
)A.8
B.6
C.4
D.2
答案:5. B
解析:
原式=$(2-1)(2+1)(2^{2}+1)(2^{4}+1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{2}-1)(2^{2}+1)(2^{4}+1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{4}-1)(2^{4}+1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{8}-1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{16}-1)(2^{16}+1)+1$
=$2^{32}-1+1$
=$2^{32}$
$2^{1}=2$,个位数字2;
$2^{2}=4$,个位数字4;
$2^{3}=8$,个位数字8;
$2^{4}=16$,个位数字6;
$2^{5}=32$,个位数字2;
个位数字以2,4,8,6循环,周期4。
$32÷4=8$,余数0,故$2^{32}$个位数字为6。
B
=$(2^{2}-1)(2^{2}+1)(2^{4}+1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{4}-1)(2^{4}+1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{8}-1)(2^{8}+1)(2^{16}+1)+1$
=$(2^{16}-1)(2^{16}+1)+1$
=$2^{32}-1+1$
=$2^{32}$
$2^{1}=2$,个位数字2;
$2^{2}=4$,个位数字4;
$2^{3}=8$,个位数字8;
$2^{4}=16$,个位数字6;
$2^{5}=32$,个位数字2;
个位数字以2,4,8,6循环,周期4。
$32÷4=8$,余数0,故$2^{32}$个位数字为6。
B
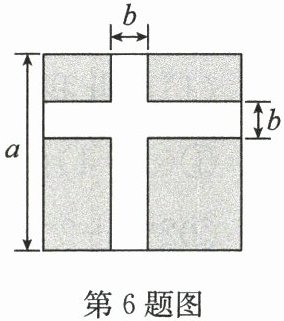
6. (2025·姑苏区期中)如图,某小区规划在边长为$a$米的正方形空地上种植草坪,为了方便行人,在空地中修建两条宽为$b$米的人行道,利用图中草坪面积的等量关系可以得到的公式是(
A.$a^{2}-2ab + b^{2}=(a - b)^{2}$
B.$a^{2}-ab = a(a - b)$
C.$a^{2}-b^{2}=(a + b)(a - b)$
D.$a^{2}+2ab + b^{2}=(a + b)^{2}$
A
)
A.$a^{2}-2ab + b^{2}=(a - b)^{2}$
B.$a^{2}-ab = a(a - b)$
C.$a^{2}-b^{2}=(a + b)(a - b)$
D.$a^{2}+2ab + b^{2}=(a + b)^{2}$
答案:6. A
解析:
解:正方形空地面积为$a^2$平方米。
两条人行道面积:横向人行道面积为$a × b$平方米,纵向人行道面积为$a × b$平方米,交叉部分面积为$b^2$平方米(重复计算,需减去),故人行道总面积为$ab + ab - b^2 = 2ab - b^2$平方米。
草坪面积 = 正方形面积 - 人行道面积,即$a^2 - (2ab - b^2) = a^2 - 2ab + b^2$平方米。
观察图形,草坪可拼成边长为$(a - b)$米的正方形,其面积为$(a - b)^2$平方米。
因此,$a^2 - 2ab + b^2 = (a - b)^2$。
A
两条人行道面积:横向人行道面积为$a × b$平方米,纵向人行道面积为$a × b$平方米,交叉部分面积为$b^2$平方米(重复计算,需减去),故人行道总面积为$ab + ab - b^2 = 2ab - b^2$平方米。
草坪面积 = 正方形面积 - 人行道面积,即$a^2 - (2ab - b^2) = a^2 - 2ab + b^2$平方米。
观察图形,草坪可拼成边长为$(a - b)$米的正方形,其面积为$(a - b)^2$平方米。
因此,$a^2 - 2ab + b^2 = (a - b)^2$。
A
7. (2025·宜兴期末)为了运用平方差公式计算$(x + 2y - 1)(x - 2y + 1)$,下列变形正确的是(
A.$[x-(2y + 1)]^{2}$
B.$[x+(2y - 1)][x-(2y - 1)]$
C.$[(xy - 2)+1][(xy - 2)-1]$
D.$[x+(2y - 1)]^{2}$
B
)A.$[x-(2y + 1)]^{2}$
B.$[x+(2y - 1)][x-(2y - 1)]$
C.$[(xy - 2)+1][(xy - 2)-1]$
D.$[x+(2y - 1)]^{2}$
答案:7. B
8. (2025·镇海区模拟)已知$(x - 2023)^{2}+(x - 2027)^{2}=34$,则$(x - 2025)^{2}$的值是(
A.5
B.9
C.13
D.17
C
)A.5
B.9
C.13
D.17
答案:8. C
解析:
设$t = x - 2025$,则$x - 2023 = t + 2$,$x - 2027 = t - 2$。
原方程可化为$(t + 2)^2 + (t - 2)^2 = 34$。
展开得$t^2 + 4t + 4 + t^2 - 4t + 4 = 34$,
合并同类项得$2t^2 + 8 = 34$,
移项得$2t^2 = 26$,
两边同时除以2得$t^2 = 13$,
即$(x - 2025)^2 = 13$。
C
原方程可化为$(t + 2)^2 + (t - 2)^2 = 34$。
展开得$t^2 + 4t + 4 + t^2 - 4t + 4 = 34$,
合并同类项得$2t^2 + 8 = 34$,
移项得$2t^2 = 26$,
两边同时除以2得$t^2 = 13$,
即$(x - 2025)^2 = 13$。
C
9. (2025·上海期末)计算$(2x - y)(x + y)$的结果为
$ 2x^{2}+xy - y^{2} $
.答案:9. $ 2x^{2}+xy - y^{2} $
解析:
$(2x - y)(x + y)$
$=2x · x + 2x · y - y · x - y · y$
$=2x^{2} + 2xy - xy - y^{2}$
$=2x^{2} + xy - y^{2}$
$=2x · x + 2x · y - y · x - y · y$
$=2x^{2} + 2xy - xy - y^{2}$
$=2x^{2} + xy - y^{2}$
10. 计算:$(-2a)^{3}·(a^{2}+3a - 1)=$
$ -8a^{5}-24a^{4}+8a^{3} $
.答案:10. $ -8a^{5}-24a^{4}+8a^{3} $
解析:
$(-2a)^{3}·(a^{2}+3a - 1)$
$=-8a^{3}·(a^{2}+3a - 1)$
$=-8a^{3}·a^{2}-8a^{3}·3a + 8a^{3}·1$
$=-8a^{5}-24a^{4}+8a^{3}$
$=-8a^{3}·(a^{2}+3a - 1)$
$=-8a^{3}·a^{2}-8a^{3}·3a + 8a^{3}·1$
$=-8a^{5}-24a^{4}+8a^{3}$