11. (2024·秦淮区期中)如果长方体的长为$3a - 4$,宽为$2a$,高为$2a$,则它的体积是
$ 12a^{3}-16a^{2} $
.答案:11. $ 12a^{3}-16a^{2} $
解析:
长方体体积 = 长×宽×高 = (3a - 4)×2a×2a = (3a - 4)×4a² = 12a³ - 16a²
12. (2024·海州区期末)已知$a - b = 2$,$ab = 5$,则$(a - 4)(b + 4)=$
$ -3 $
.答案:12. $ -3 $
解析:
$(a - 4)(b + 4)$
$=ab + 4a - 4b - 16$
$=ab + 4(a - b) - 16$
因为$a - b = 2$,$ab = 5$,所以原式$=5 + 4×2 - 16 = 5 + 8 - 16 = -3$
$=ab + 4a - 4b - 16$
$=ab + 4(a - b) - 16$
因为$a - b = 2$,$ab = 5$,所以原式$=5 + 4×2 - 16 = 5 + 8 - 16 = -3$
13. 如果$x^{2}-y^{2}=8$,$x - y = 2$,那么代数式$x^{2}+y^{2}$的值是
$ 10 $
.答案:13. $ 10 $
解析:
因为$x^{2}-y^{2}=(x + y)(x - y)=8$,且$x - y = 2$,所以$x + y = 8÷2 = 4$。联立$\begin{cases}x + y = 4 \\ x - y = 2\end{cases}$,两式相加得$2x = 6$,解得$x = 3$,将$x = 3$代入$x - y = 2$,得$y = 1$。则$x^{2}+y^{2}=3^{2}+1^{2}=9 + 1 = 10$。
14. 若$x^{2}+ax + 25$是关于$x$的完全平方式,则$a =$
$ \pm 10 $
.答案:14. $ \pm 10 $
解析:
$x^{2}+ax + 25$是完全平方式,可表示为$(x\pm5)^{2}$。
$(x + 5)^{2}=x^{2}+10x + 25$,则$a = 10$;
$(x - 5)^{2}=x^{2}-10x + 25$,则$a=-10$。
综上,$a = \pm 10$。
$(x + 5)^{2}=x^{2}+10x + 25$,则$a = 10$;
$(x - 5)^{2}=x^{2}-10x + 25$,则$a=-10$。
综上,$a = \pm 10$。
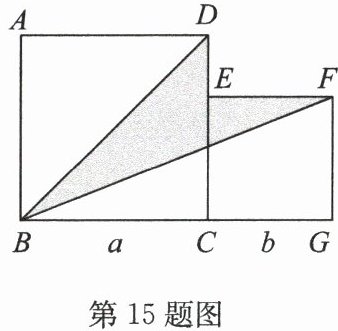
15. (2024·吴中区期中)如图,两个正方形的边长分别为$a$,$b$,若$a + b = 5$,$ab = 6$,则阴影部分的面积为
$ 3.5 $
.
答案:15. $ 3.5 $
解析:
解:阴影部分面积为两个正方形面积之和减去三个空白三角形面积。
两个正方形面积和:$a^2 + b^2$。
空白三角形面积分别为:
$S_{△ ABD}=\frac{1}{2}a^2$
$S_{△ BGF}=\frac{1}{2}(a + b)b$
$S_{△ DEF}=\frac{1}{2}b(a - b)$
阴影面积$S = a^2 + b^2 - \frac{1}{2}a^2 - \frac{1}{2}(a + b)b - \frac{1}{2}b(a - b)$,化简得$S=\frac{1}{2}(a^2 + b^2 - ab)$。
已知$a + b = 5$,$ab = 6$,则$a^2 + b^2=(a + b)^2 - 2ab=25 - 12 = 13$。
所以$S=\frac{1}{2}(13 - 6)=\frac{7}{2}=3.5$。
$3.5$
两个正方形面积和:$a^2 + b^2$。
空白三角形面积分别为:
$S_{△ ABD}=\frac{1}{2}a^2$
$S_{△ BGF}=\frac{1}{2}(a + b)b$
$S_{△ DEF}=\frac{1}{2}b(a - b)$
阴影面积$S = a^2 + b^2 - \frac{1}{2}a^2 - \frac{1}{2}(a + b)b - \frac{1}{2}b(a - b)$,化简得$S=\frac{1}{2}(a^2 + b^2 - ab)$。
已知$a + b = 5$,$ab = 6$,则$a^2 + b^2=(a + b)^2 - 2ab=25 - 12 = 13$。
所以$S=\frac{1}{2}(13 - 6)=\frac{7}{2}=3.5$。
$3.5$
16. (2025·宿城区期末)用简便方法计算:$\frac{1}{4}×(6.16)^{2}-4×(1.04)^{2}=$
$ 5.16 $
.答案:16. $ 5.16 $
解析:
$\frac{1}{4} × (6.16)^2 - 4 × (1.04)^2$
$=(\frac{1}{2} × 6.16)^2 - (2 × 1.04)^2$
$=(3.08)^2 - (2.08)^2$
$=(3.08 - 2.08)(3.08 + 2.08)$
$=1 × 5.16$
$=5.16$
$=(\frac{1}{2} × 6.16)^2 - (2 × 1.04)^2$
$=(3.08)^2 - (2.08)^2$
$=(3.08 - 2.08)(3.08 + 2.08)$
$=1 × 5.16$
$=5.16$
17. (2025·宿豫区期中)数形结合思想是最重要的数学思想之一,也是数学解题的重要方法.结合图形,写出$(2a + b + c)^{2}=$
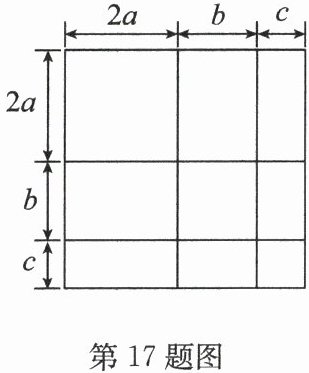
$ 4a^{2}+b^{2}+c^{2}+4ab + 4ac + 2bc $
.
答案:17. $ 4a^{2}+b^{2}+c^{2}+4ab + 4ac + 2bc $
18. 规律探究(2025·海淀区期末)我国南宋数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了$(a + b)^{n}$($n$为非负整数)展开式的项数及各项系数的有关规律.$(x - 2)^{5}$的展开式中$x$的一次项系数是

$ 80 $
.
答案:18. $ 80 $
解析:
$(x - 2)^{5}$展开式的通项为$T_{r+1}=\binom{5}{r}x^{5-r}(-2)^{r}$。令$5 - r = 1$,得$r = 4$。则一次项系数为$\binom{5}{4}(-2)^{4}=5×16 = 80$。
80
80
19. (12分)(2024·江宁区期末)计算:
(1)$x(x + 7)-(x - 3)(x + 2)$;
(2)$(a + 4)(a - 4)-(a - 1)^{2}$;
(3)$(m - 2n)^{2}(m + 2n)^{2}$;
(4)$(a - 2b - c)(a + 2b - c)$.
(1)$x(x + 7)-(x - 3)(x + 2)$;
(2)$(a + 4)(a - 4)-(a - 1)^{2}$;
(3)$(m - 2n)^{2}(m + 2n)^{2}$;
(4)$(a - 2b - c)(a + 2b - c)$.
答案:19. 解: (1) 原式 $ =x^{2}+7x-(x^{2}-x - 6)=x^{2}+7x - x^{2}+x + 6=8x + 6 $.
(2) 原式 $ =a^{2}-16-(a^{2}-2a + 1)=a^{2}-16 - a^{2}+2a - 1=2a - 17 $.
(3) 原式 $ =[(m - 2n)(m + 2n)]^{2}=(m^{2}-4n^{2})^{2}=m^{4}-8m^{2}n^{2}+16n^{4} $.
(4) 原式 $ =[(a - c)-2b][(a - c)+2b]=(a - c)^{2}-(2b)^{2}=a^{2}-2ac + c^{2}-4b^{2} $.
(2) 原式 $ =a^{2}-16-(a^{2}-2a + 1)=a^{2}-16 - a^{2}+2a - 1=2a - 17 $.
(3) 原式 $ =[(m - 2n)(m + 2n)]^{2}=(m^{2}-4n^{2})^{2}=m^{4}-8m^{2}n^{2}+16n^{4} $.
(4) 原式 $ =[(a - c)-2b][(a - c)+2b]=(a - c)^{2}-(2b)^{2}=a^{2}-2ac + c^{2}-4b^{2} $.