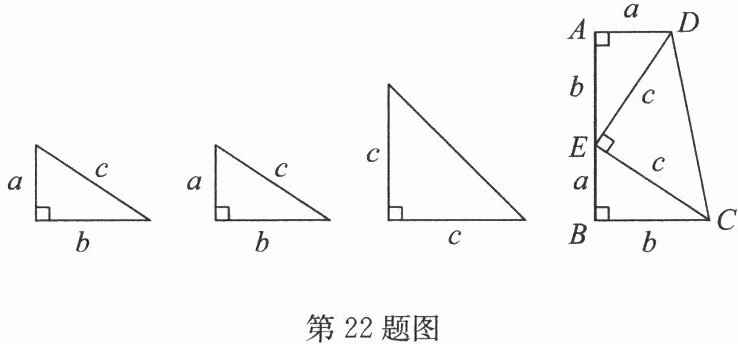
22. (8分)数学活动中,小明和同学动手拼图发现:两个边长分别为$a$,$b$,$c$的直角三角形和一个两条直角边都是$c$的直角三角形可以拼成如图所示的直角梯形.
(1)请你用两种不同的方法计算这个图形的面积,你能发现$a$,$b$,$c$之间有什么数量关系吗?请说明理由.
(2)若这个直角梯形的上、下底之差为$1\mathrm{cm}$,高为$7\mathrm{cm}$,请计算$△ DEC$的面积.
(1)请你用两种不同的方法计算这个图形的面积,你能发现$a$,$b$,$c$之间有什么数量关系吗?请说明理由.
(2)若这个直角梯形的上、下底之差为$1\mathrm{cm}$,高为$7\mathrm{cm}$,请计算$△ DEC$的面积.

答案:22. 解: (1) $ a^{2}+b^{2}=c^{2} $, 理由如下:
梯形的面积为 $ \frac{1}{2}(a + b)(a + b)=\frac{1}{2}(a + b)^{2} $.
三个三角形的面积和为 $ \frac{1}{2}ab×2+\frac{1}{2}c· c=ab+\frac{1}{2}c^{2} $,
所以 $ \frac{1}{2}(a + b)^{2}=ab+\frac{1}{2}c^{2} $, 整理, 得 $ a^{2}+b^{2}=c^{2} $.
(2) 设上底长为 $ x\ \mathrm{cm} $, 则下底长为 $ (x + 1)\mathrm{cm} $.
因为高为 $ 7\ \mathrm{cm} $, 所以 $ x + x + 1=7 $,
所以 $ x = 3 $, $ x + 1 = 4 $,
所以 $ S_{△ DEC}=\frac{1}{2}×(3^{2}+4^{2})=\frac{25}{2}(\mathrm{cm}^{2}) $.
梯形的面积为 $ \frac{1}{2}(a + b)(a + b)=\frac{1}{2}(a + b)^{2} $.
三个三角形的面积和为 $ \frac{1}{2}ab×2+\frac{1}{2}c· c=ab+\frac{1}{2}c^{2} $,
所以 $ \frac{1}{2}(a + b)^{2}=ab+\frac{1}{2}c^{2} $, 整理, 得 $ a^{2}+b^{2}=c^{2} $.
(2) 设上底长为 $ x\ \mathrm{cm} $, 则下底长为 $ (x + 1)\mathrm{cm} $.
因为高为 $ 7\ \mathrm{cm} $, 所以 $ x + x + 1=7 $,
所以 $ x = 3 $, $ x + 1 = 4 $,
所以 $ S_{△ DEC}=\frac{1}{2}×(3^{2}+4^{2})=\frac{25}{2}(\mathrm{cm}^{2}) $.
23. (10分)你能求$(x - 1)(x^{2015}+x^{2014}+x^{2013}+x^{2012}+···+x + 1)$的值吗?遇到这样的问题,我们可以先思考从简单的情形入手.
①$(x - 1)(x + 1)=x^{2}-1$;
②$(x - 1)(x^{2}+x + 1)=x^{3}-1$;
③$(x - 1)(x^{3}+x^{2}+x + 1)=x^{4}-1$;
……
(1)由此我们可以得到:
①$(x - 1)(x^{2015}+x^{2014}+x^{2013}+x^{2012}+···+x + 1)=$
②$2^{100}+2^{99}+2^{98}+2^{97}+···+2 + 1=$
(2)请利用上面的结论,完成下面的计算:
$x[(x + 1)^{2025}+(x + 1)^{2024}+(x + 1)^{2023}+(x + 1)^{2022}···+(x + 1)+1]$.
①$(x - 1)(x + 1)=x^{2}-1$;
②$(x - 1)(x^{2}+x + 1)=x^{3}-1$;
③$(x - 1)(x^{3}+x^{2}+x + 1)=x^{4}-1$;
……
(1)由此我们可以得到:
①$(x - 1)(x^{2015}+x^{2014}+x^{2013}+x^{2012}+···+x + 1)=$
$ x^{2016}-1 $
;②$2^{100}+2^{99}+2^{98}+2^{97}+···+2 + 1=$
$ 2^{101}-1 $
.(2)请利用上面的结论,完成下面的计算:
$x[(x + 1)^{2025}+(x + 1)^{2024}+(x + 1)^{2023}+(x + 1)^{2022}···+(x + 1)+1]$.
答案:23. (1) ① $ x^{2016}-1 $
② $ 2^{101}-1 $
(2) 解: 原式 $ =[(x + 1)-1][(x + 1)^{2025}+(x + 1)^{2024}+(x + 1)^{2023}+(x + 1)^{2022}+···+(x + 1)+1]=(x + 1)^{2026}-1 $.
② $ 2^{101}-1 $
(2) 解: 原式 $ =[(x + 1)-1][(x + 1)^{2025}+(x + 1)^{2024}+(x + 1)^{2023}+(x + 1)^{2022}+···+(x + 1)+1]=(x + 1)^{2026}-1 $.