1. 下图是2024年巴黎奥运会,即第33届夏季奥林匹克运动会比赛项目运动图标,其中属于轴对称图形的是(
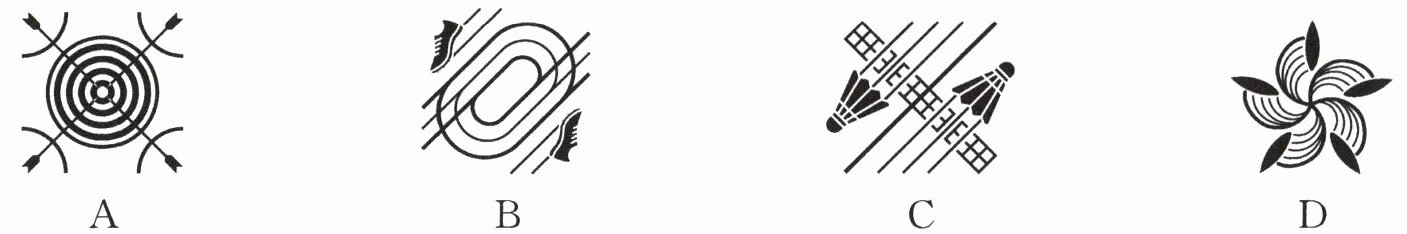
A
)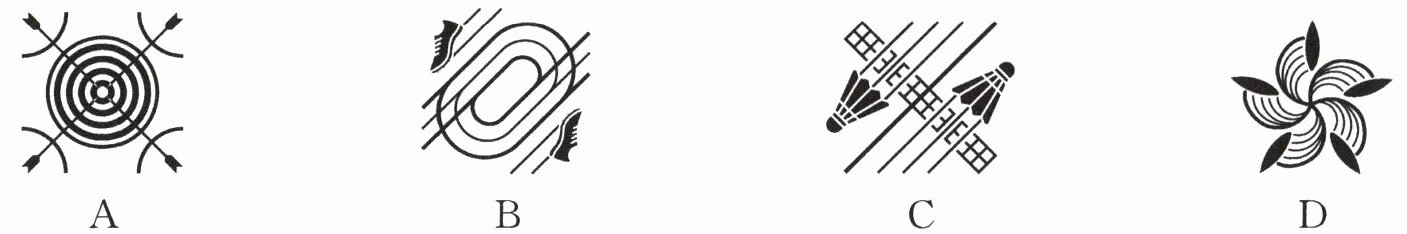
答案:1. A
2. 下列正多边形中,绕其中心旋转45°后,能和自身重合的是(
A.正三角形
B.正六边形
C.正方形
D.正八边形
D
)A.正三角形
B.正六边形
C.正方形
D.正八边形
答案:2. D
解析:
正多边形绕中心旋转能与自身重合的最小角度为$\frac{360°}{n}$($n$为边数)。
正三角形:$\frac{360°}{3}=120°$,$45°$不是$120°$的整数倍,不符合。
正六边形:$\frac{360°}{6}=60°$,$45°$不是$60°$的整数倍,不符合。
正方形:$\frac{360°}{4}=90°$,$45°$不是$90°$的整数倍,不符合。
正八边形:$\frac{360°}{8}=45°$,$45°$是$45°$的整数倍,符合。
D
正三角形:$\frac{360°}{3}=120°$,$45°$不是$120°$的整数倍,不符合。
正六边形:$\frac{360°}{6}=60°$,$45°$不是$60°$的整数倍,不符合。
正方形:$\frac{360°}{4}=90°$,$45°$不是$90°$的整数倍,不符合。
正八边形:$\frac{360°}{8}=45°$,$45°$是$45°$的整数倍,符合。
D
3. (2025·宿城区期中)下列图形中既是轴对称图形又是中心对称图形的是(

D
)
答案:3. D
4. (2025·建邺区期中)如图,将△ABC沿BC方向平移4cm得到△DEF.若BF=7CE,则BC的长为(
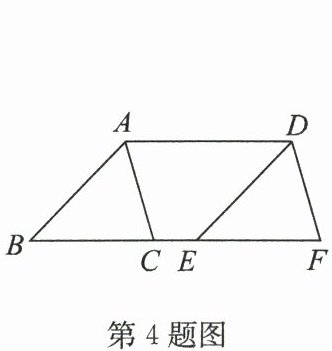
A.2cm
B.2.5cm
C.3cm
D.3.5cm
C
)
A.2cm
B.2.5cm
C.3cm
D.3.5cm
答案:4. C
解析:
证明:
∵△ABC沿BC方向平移4cm得到△DEF,
∴BC=EF,平移距离为4cm,即BE=4cm。
设CE=x cm,则BF=7x cm。
∵BF=BE+EF,EF=BC,BE=4cm,
∴7x=4+BC。
又
∵BC=BE-CE=4-x,
∴7x=4+(4-x),
7x=8-x,
8x=8,
x=1。
∴BC=4-x=4-1=3cm。
答案:C
∵△ABC沿BC方向平移4cm得到△DEF,
∴BC=EF,平移距离为4cm,即BE=4cm。
设CE=x cm,则BF=7x cm。
∵BF=BE+EF,EF=BC,BE=4cm,
∴7x=4+BC。
又
∵BC=BE-CE=4-x,
∴7x=4+(4-x),
7x=8-x,
8x=8,
x=1。
∴BC=4-x=4-1=3cm。
答案:C
5. 一个图形经过旋转变换,下列说法中:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有改变.正确的有(
A.4个
B.3个
C.2个
D.1个
B
)A.4个
B.3个
C.2个
D.1个
答案:5. B
解析:
②对应线段相等;③对应角相等;④图形的形状和大小都没有改变,正确的有3个。
B
B
6. (2025·高淳区期末)将一圆形纸片对折后再对折得到如图所示的扇形,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是(

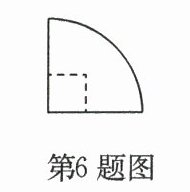
A
)

答案:6. A