7. (2024·金坛区期末)如图,在四边形ABCD中,AD=CD,AB=CB,我们把这种两组邻边分别相等的四边形叫作“筝形”.下列关于“筝形”的结论错误的是(
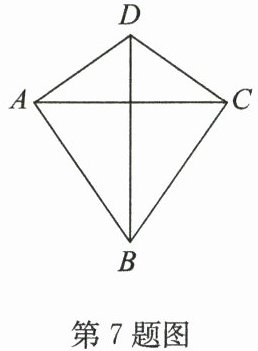
A.对角线AC,BD互相垂直平分
B.直线BD是筝形的对称轴
C.对角线BD平分∠ABC
D.筝形的面积等于对角线AC与BD的乘积的一半
A
)
A.对角线AC,BD互相垂直平分
B.直线BD是筝形的对称轴
C.对角线BD平分∠ABC
D.筝形的面积等于对角线AC与BD的乘积的一半
答案:7. A
解析:
证明:
在筝形$ABCD$中,$AD=CD$,$AB=CB$,$AC$为公共边,
$\therefore △ ABC ≌ △ ADC$(SSS),
$\therefore ∠ BAC = ∠ DAC$,$∠ BCA = ∠ DCA$,
$\therefore AC$平分$∠ BAD$和$∠ BCD$。
设$AC$与$BD$交于点$O$,
在$△ ABO$和$△ ADO$中,
$\because AB=AD$,$∠ BAO = ∠ DAO$,$AO=AO$,
$\therefore △ ABO ≌ △ ADO$(SAS),
$\therefore BO=DO$,$∠ AOB = ∠ AOD = 90°$,
$\therefore AC ⊥ BD$,$BD$被$AC$平分,但$AC$不一定被$BD$平分(只有当$AB=AD$时才平分),故A错误。
$\because △ ABO ≌ △ ADO$,$△ CBO ≌ △ CDO$,
$\therefore$直线$BD$是筝形的对称轴,B正确。
$\because △ ABO ≌ △ ADO$,$\therefore ∠ ABO = ∠ ADO$,同理$∠ CBO = ∠ CDO$,
$\therefore BD$平分$∠ ABC$和$∠ ADC$,C正确。
筝形面积$S = S_{△ ABC} + S_{△ ADC} = \frac{1}{2}AC · BO + \frac{1}{2}AC · DO = \frac{1}{2}AC · (BO + DO) = \frac{1}{2}AC · BD$,D正确。
结论错误的是A。
答案:A
在筝形$ABCD$中,$AD=CD$,$AB=CB$,$AC$为公共边,
$\therefore △ ABC ≌ △ ADC$(SSS),
$\therefore ∠ BAC = ∠ DAC$,$∠ BCA = ∠ DCA$,
$\therefore AC$平分$∠ BAD$和$∠ BCD$。
设$AC$与$BD$交于点$O$,
在$△ ABO$和$△ ADO$中,
$\because AB=AD$,$∠ BAO = ∠ DAO$,$AO=AO$,
$\therefore △ ABO ≌ △ ADO$(SAS),
$\therefore BO=DO$,$∠ AOB = ∠ AOD = 90°$,
$\therefore AC ⊥ BD$,$BD$被$AC$平分,但$AC$不一定被$BD$平分(只有当$AB=AD$时才平分),故A错误。
$\because △ ABO ≌ △ ADO$,$△ CBO ≌ △ CDO$,
$\therefore$直线$BD$是筝形的对称轴,B正确。
$\because △ ABO ≌ △ ADO$,$\therefore ∠ ABO = ∠ ADO$,同理$∠ CBO = ∠ CDO$,
$\therefore BD$平分$∠ ABC$和$∠ ADC$,C正确。
筝形面积$S = S_{△ ABC} + S_{△ ADC} = \frac{1}{2}AC · BO + \frac{1}{2}AC · DO = \frac{1}{2}AC · (BO + DO) = \frac{1}{2}AC · BD$,D正确。
结论错误的是A。
答案:A
8. 如图,将△ABC绕着点A逆时针旋转65°,得到△AED.若∠E=35°,AD//BC,有下列结论:①AC=AD;②∠BAE=80°;③BC=AE;④∠D=65°.其中正确的有(
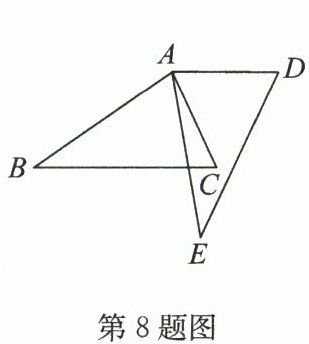
A.4个
B.3个
C.2个
D.1个
C
)
A.4个
B.3个
C.2个
D.1个
答案:8. C
9. 如图,把△ABC沿BC方向向右平移2cm到△DEF的位置,AC与DF的关系是
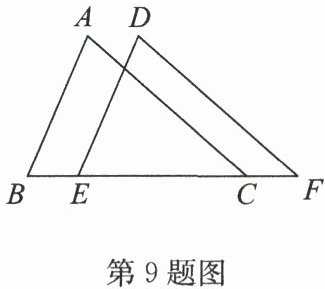
平行且相等
,BE+CF=4
cm.
答案:9. 平行且相等 4
10. 如图,将长为6,宽为4的长方形ABCD先向右平移2个单位长度,再向下平移1个单位长度,得到长方形A'B'C'D',则阴影部分的面积为
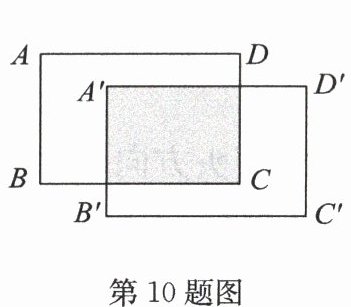
12
.
答案:10. 12
解析:
解:长方形ABCD长为6,宽为4。向右平移2个单位,向下平移1个单位后,阴影部分的长为$6 - 2 = 4$,宽为$4 - 1 = 3$,面积为$4×3 = 12$。
12
12
11. (2025·兴化期末)如图是“赵爽弦图”.有下列关于“赵爽弦图”的说法:①只是轴对称图形;②只是中心对称图形;③既是轴对称图形又是中心对称图形;④该图形绕着某个点旋转90°后能与自身重合.其中正确的是
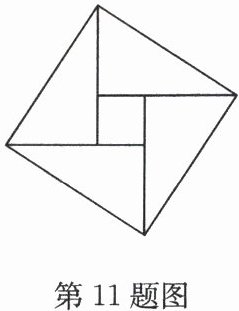
②④
.(填序号)
答案:11. ②④
12. 如图,AO所在的直线是△ABC的对称轴,点D,E是AO上的两点,已知图中阴影部分的面积为9,则△ABC的面积为.
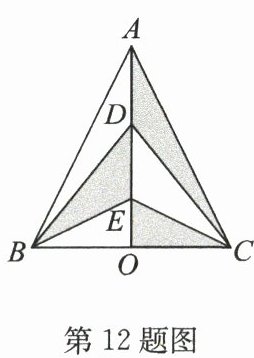

答案:18
解析:
∵AO是△ABC的对称轴,∴△ABC关于AO对称,即△ABO≌△ACO,S△ABO=S△ACO=1/2S△ABC。
∵D,E在AO上,∴△ABD≌△ACD,△BDE≌△CDE,设S△ABD=S△ACD=a,S△BDE=S△CDE=b。
阴影部分面积=S△ABD+S△ACD+S△BDE+S△CDE=2a+2b=9,∴a+b=4.5。
S△ABO=S△ABD+S△BDE+S△BOE,S△ACO=S△ACD+S△CDE+S△COE,又S△BOE=S△COE(对称),设S△BOE=S△COE=c。
则S△ABO=a+b+c=4.5+c,S△ABC=2S△ABO=2(4.5+c)=9+2c。
又∵阴影部分若包含△BOE和△COE,则阴影面积=2a+2b+2c=9+2c=9,∴2c=0,即E与O重合。
此时S△ABC=9+0=9?矛盾,故阴影部分为2(a+b)=9,而△ABC面积=2(a+b+c)+2c?不对。
重新考虑:AO为对称轴,阴影部分关于AO对称,面积为9,故对称轴一侧阴影面积为4.5。△ABC面积为对称轴一侧总面积的2倍,而一侧总面积=阴影面积+非阴影面积,若阴影部分为一侧全部,则△ABC面积=2×9=18。
∵D,E在AO上,∴△ABD≌△ACD,△BDE≌△CDE,设S△ABD=S△ACD=a,S△BDE=S△CDE=b。
阴影部分面积=S△ABD+S△ACD+S△BDE+S△CDE=2a+2b=9,∴a+b=4.5。
S△ABO=S△ABD+S△BDE+S△BOE,S△ACO=S△ACD+S△CDE+S△COE,又S△BOE=S△COE(对称),设S△BOE=S△COE=c。
则S△ABO=a+b+c=4.5+c,S△ABC=2S△ABO=2(4.5+c)=9+2c。
又∵阴影部分若包含△BOE和△COE,则阴影面积=2a+2b+2c=9+2c=9,∴2c=0,即E与O重合。
此时S△ABC=9+0=9?矛盾,故阴影部分为2(a+b)=9,而△ABC面积=2(a+b+c)+2c?不对。
重新考虑:AO为对称轴,阴影部分关于AO对称,面积为9,故对称轴一侧阴影面积为4.5。△ABC面积为对称轴一侧总面积的2倍,而一侧总面积=阴影面积+非阴影面积,若阴影部分为一侧全部,则△ABC面积=2×9=18。
13. (2025·宿城区期中)有下列图形:线段,角,长方形,梯形,平行四边形,圆,等边三角形.其中,既是轴对称图形又是中心对称图形的有个.
答案:线段:是轴对称图形(对称轴为线段垂直平分线和线段所在直线),也是中心对称图形(对称中心为线段中点)。
角:是轴对称图形(对称轴为角平分线所在直线),不是中心对称图形。
长方形:是轴对称图形(对称轴为对边中点连线所在直线),也是中心对称图形(对称中心为对角线交点)。
梯形:一般梯形不是轴对称图形也不是中心对称图形;等腰梯形是轴对称图形(对称轴为两底中点连线所在直线),但不是中心对称图形。题目中未明确梯形类型,按一般梯形处理,故梯形既不是轴对称图形也不是中心对称图形。
平行四边形:不是轴对称图形(特殊平行四边形如矩形、菱形、正方形除外,但题目中平行四边形为一般平行四边形),是中心对称图形(对称中心为对角线交点)。
圆:是轴对称图形(任意一条直径所在直线都是对称轴),也是中心对称图形(对称中心为圆心)。
等边三角形:是轴对称图形(对称轴为三条高所在直线),不是中心对称图形。
综上,既是轴对称图形又是中心对称图形的有线段、长方形、圆,共3个。
3
角:是轴对称图形(对称轴为角平分线所在直线),不是中心对称图形。
长方形:是轴对称图形(对称轴为对边中点连线所在直线),也是中心对称图形(对称中心为对角线交点)。
梯形:一般梯形不是轴对称图形也不是中心对称图形;等腰梯形是轴对称图形(对称轴为两底中点连线所在直线),但不是中心对称图形。题目中未明确梯形类型,按一般梯形处理,故梯形既不是轴对称图形也不是中心对称图形。
平行四边形:不是轴对称图形(特殊平行四边形如矩形、菱形、正方形除外,但题目中平行四边形为一般平行四边形),是中心对称图形(对称中心为对角线交点)。
圆:是轴对称图形(任意一条直径所在直线都是对称轴),也是中心对称图形(对称中心为圆心)。
等边三角形:是轴对称图形(对称轴为三条高所在直线),不是中心对称图形。
综上,既是轴对称图形又是中心对称图形的有线段、长方形、圆,共3个。
3
14. 正方形既是轴对称图形,又是中心对称图形,它有条对称轴,对称中心是.
答案:4;两条对角线的交点
15. (2024·泰兴期中)如图,P为∠AOB内一点,分别作出点P关于OA,OB的对称点P₁,P₂,连接P₁P₂交OA于点M,交OB于点N,连接PM,PN.若P₁P₂=12,则△PMN的周长为.
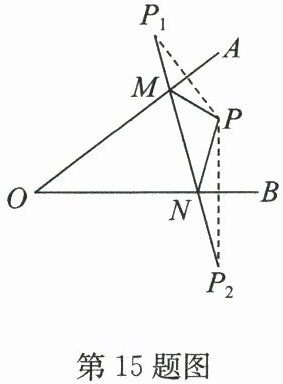

答案:∵点P关于OA的对称点为P₁,
∴OA垂直平分PP₁,
∴PM = P₁M。
∵点P关于OB的对称点为P₂,
∴OB垂直平分PP₂,
∴PN = P₂N。
∵P₁P₂ = 12,
∴△PMN的周长 = PM + MN + PN = P₁M + MN + P₂N = P₁P₂ = 12。
12
∴OA垂直平分PP₁,
∴PM = P₁M。
∵点P关于OB的对称点为P₂,
∴OB垂直平分PP₂,
∴PN = P₂N。
∵P₁P₂ = 12,
∴△PMN的周长 = PM + MN + PN = P₁M + MN + P₂N = P₁P₂ = 12。
12
16. 张老汉打算在院落里种上蔬菜.如图,院落为东西长32m,南北宽20m的长方形.为了行走方便,要修筑同样宽的三条道路,余下的部分要种上蔬菜,若每条道路的宽均为1m,则蔬菜的总种植面积是.
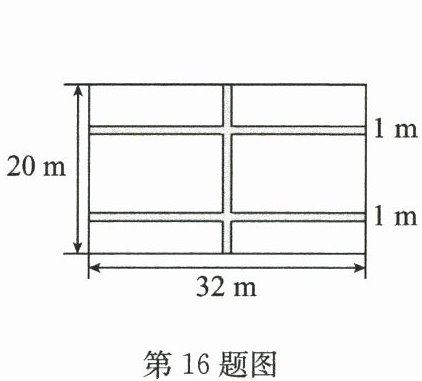

答案:总面积:32×20=640(m²)
道路面积:横向道路1条,面积32×1=32(m²);纵向道路2条,每条面积20×1=20(m²),两条共40(m²)。交叉部分2处,每处1×1=1(m²),共2(m²)。
道路总面积:32+40-2=70(m²)
蔬菜种植面积:640-70=570(m²)
570
道路面积:横向道路1条,面积32×1=32(m²);纵向道路2条,每条面积20×1=20(m²),两条共40(m²)。交叉部分2处,每处1×1=1(m²),共2(m²)。
道路总面积:32+40-2=70(m²)
蔬菜种植面积:640-70=570(m²)
570