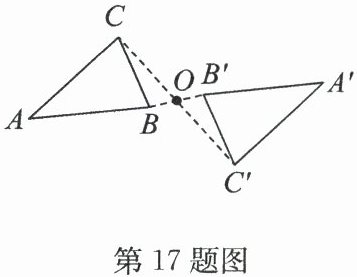
17. (2025·秦淮区期末)如图,△ABC与△A'B'C'关于点O成中心对称,有下列结论:①线段AA'与线段CC'互相平分;②∠BCO=∠B'C'O;③AC//A'C';④∠ABC=∠A'C'B'.其中正确的是.(填序号)

答案:①由于$\bigtriangleup ABC$与$\bigtriangleup A^{\prime}B^{\prime}C^{\prime}$关于点$O$成中心对称,
根据中心对称图形的性质,线段$AA^{\prime}$和线段$CC^{\prime}$都会经过对称中心$O$,并且被$O$平分。
所以,线段$AA^{\prime}$与线段$CC^{\prime}$互相平分,故①正确。
②由于中心对称,我们有$\bigtriangleup ABC ≌ \bigtriangleup A^{\prime}B^{\prime}C^{\prime}$。
从对称性,我们知道$OB = OB^{\prime}$,$OC = OC^{\prime}$,且$∠ BOC = ∠ B^{\prime}OC^{\prime}$。
根据三角形的全等性质,我们得到$∠ BCO = ∠ B^{\prime}C^{\prime}O$,故②正确。
③由于$\bigtriangleup ABC ≌ \bigtriangleup A^{\prime}B^{\prime}C^{\prime}$,
根据全等三角形的对应角相等,我们有$∠ A = ∠ A^{\prime}$。
由于线段$AA^{\prime}$和$CC^{\prime}$被$O$平分,
根据平行线的交替内角性质,我们得到$AC // A^{\prime}C^{\prime}$,故③正确。
④从$\bigtriangleup ABC ≌ \bigtriangleup A^{\prime}B^{\prime}C^{\prime}$,
我们只能得到对应角相等,即$∠ ABC = ∠ A^{\prime}B^{\prime}C^{\prime}$,
并不能直接得到$∠ ABC = ∠ A^{\prime}C^{\prime}B^{\prime}$,故④错误。
故答案为:①②③。
根据中心对称图形的性质,线段$AA^{\prime}$和线段$CC^{\prime}$都会经过对称中心$O$,并且被$O$平分。
所以,线段$AA^{\prime}$与线段$CC^{\prime}$互相平分,故①正确。
②由于中心对称,我们有$\bigtriangleup ABC ≌ \bigtriangleup A^{\prime}B^{\prime}C^{\prime}$。
从对称性,我们知道$OB = OB^{\prime}$,$OC = OC^{\prime}$,且$∠ BOC = ∠ B^{\prime}OC^{\prime}$。
根据三角形的全等性质,我们得到$∠ BCO = ∠ B^{\prime}C^{\prime}O$,故②正确。
③由于$\bigtriangleup ABC ≌ \bigtriangleup A^{\prime}B^{\prime}C^{\prime}$,
根据全等三角形的对应角相等,我们有$∠ A = ∠ A^{\prime}$。
由于线段$AA^{\prime}$和$CC^{\prime}$被$O$平分,
根据平行线的交替内角性质,我们得到$AC // A^{\prime}C^{\prime}$,故③正确。
④从$\bigtriangleup ABC ≌ \bigtriangleup A^{\prime}B^{\prime}C^{\prime}$,
我们只能得到对应角相等,即$∠ ABC = ∠ A^{\prime}B^{\prime}C^{\prime}$,
并不能直接得到$∠ ABC = ∠ A^{\prime}C^{\prime}B^{\prime}$,故④错误。
故答案为:①②③。
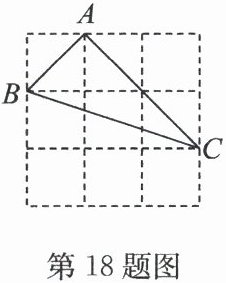
18. (2025·钟吾初中月考)如图的3×3的正方形网格中,△ABC的顶点都在小正方形的顶点上,这样的三角形称为格点三角形,在网格中与△ABC关于某直线成轴对称的格点三角形一共有个.

答案:5
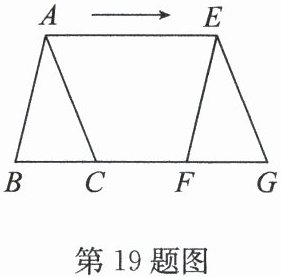
19. (6分)如图,△EFG是由△ABC沿箭头方向平移得到的.
(1)若∠BAC=35°,求∠FEG的度数;
(2)若EG=2cm,求AC的长;
(3)若AE=2.5cm,求BF,CG的长.
(1)若∠BAC=35°,求∠FEG的度数;
(2)若EG=2cm,求AC的长;
(3)若AE=2.5cm,求BF,CG的长.

答案:(1) 由于△EFG是由△ABC平移得到的,平移不改变角的度数,
所以,$∠ FEG = ∠ BAC = 35°$。
(2) 由于△EFG是由△ABC平移得到的,平移不改变线段的长度,
所以,$AC = EG = 2 \mathrm{cm}$。
(3) 由于△EFG是由△ABC平移得到的,平移距离相等,
所以,$AE = BF = CG = 2.5 \mathrm{cm}$。
所以,$∠ FEG = ∠ BAC = 35°$。
(2) 由于△EFG是由△ABC平移得到的,平移不改变线段的长度,
所以,$AC = EG = 2 \mathrm{cm}$。
(3) 由于△EFG是由△ABC平移得到的,平移距离相等,
所以,$AE = BF = CG = 2.5 \mathrm{cm}$。
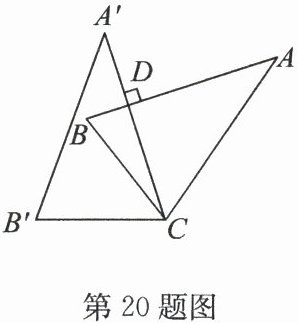
20. (8分)如图,在△ABC中,∠B=70°,将△ABC绕点C逆时针旋转52°得到△A'B'C,且AB⊥A'C于点D,求∠A'CB'的度数.

答案:72°
解析:
∵△ABC绕点C逆时针旋转52°得到△A'B'C,
∴∠ACA'=52°(旋转角),∠A'CB'=∠ACB(对应角相等)。
∵AB⊥A'C于点D,
∴∠ADC=90°。
在Rt△ADC中,∠A+∠ACD=90°,
又∵∠ACD=∠ACA'=52°,
∴∠A=90°-52°=38°。
在△ABC中,∠A+∠B+∠ACB=180°,∠B=70°,
∴∠ACB=180°-∠A-∠B=180°-38°-70°=72°。
∴∠A'CB'=∠ACB=72°。
∴∠ACA'=52°(旋转角),∠A'CB'=∠ACB(对应角相等)。
∵AB⊥A'C于点D,
∴∠ADC=90°。
在Rt△ADC中,∠A+∠ACD=90°,
又∵∠ACD=∠ACA'=52°,
∴∠A=90°-52°=38°。
在△ABC中,∠A+∠B+∠ACB=180°,∠B=70°,
∴∠ACB=180°-∠A-∠B=180°-38°-70°=72°。
∴∠A'CB'=∠ACB=72°。
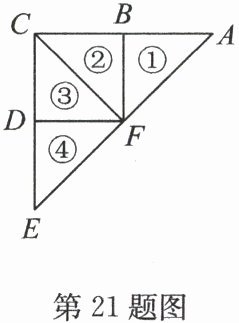
21. (8分)如图所示的图形是由四个能够完全重合的等腰直角三角形拼成的,认真观察后,解答下列问题:
(1)图中有哪些三角形关于直线CF成轴对称?
(2)图中有哪些三角形可以由三角形①旋转得到?写出相应的旋转中心和旋转角度.
(3)图中有哪些三角形可以由三角形①平移得到?说出平移的方向和距离.
(1)图中有哪些三角形关于直线CF成轴对称?
(2)图中有哪些三角形可以由三角形①旋转得到?写出相应的旋转中心和旋转角度.
(3)图中有哪些三角形可以由三角形①平移得到?说出平移的方向和距离.

答案:答案略
解析:
(1)三角形①与三角形②关于直线CF成轴对称。
(2)三角形②可以由三角形①以点F为旋转中心,顺时针旋转90°得到;三角形③可以由三角形①以点F为旋转中心,顺时针旋转180°得到;三角形④可以由三角形①以点F为旋转中心,顺时针旋转270°得到。
(3)无三角形可以由三角形①平移得到。
(2)三角形②可以由三角形①以点F为旋转中心,顺时针旋转90°得到;三角形③可以由三角形①以点F为旋转中心,顺时针旋转180°得到;三角形④可以由三角形①以点F为旋转中心,顺时针旋转270°得到。
(3)无三角形可以由三角形①平移得到。