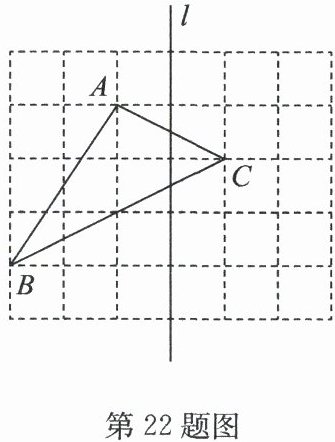
22. (8分)如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C在小正方形的顶点上.
(1)△ABC的面积为;
(2)在图中画出与△ABC关于直线l成轴对称的△A'B'C';
(3)在直线l上找一点P,使PA+PB的长最短.
(1)△ABC的面积为;
(2)在图中画出与△ABC关于直线l成轴对称的△A'B'C';
(3)在直线l上找一点P,使PA+PB的长最短.

答案:(1)
用正方格纸中割补法:
完整方格为:$3×3=9$,
三角形外多算小三角形面积:$1+1.5+2=4.5$,
$\bigtriangleup ABC$面积= $ 4 × 3 - \frac{1}{2} × 1 × 3 - \frac{1}{2} × 2 × 3 - \frac{1}{2} × 1 × 2 - 1$,
即$12 - 1.5 - 3 - 1 - 1 = 5 - 0.5= 5$。
或直接计算:
$\bigtriangleup ABC面积 = \frac{1}{2} × 底 × 高 = \frac{1}{2} × 2 × 3 - 1× 2= 5 - (补上计算多余部分)= 5$。
答案为:$5$。
(2)
$A^{\prime} (2, 4)$,
$B^{\prime} (-1, 1)$,
$C^{\prime} (2, 2)$。
(3)
点 $P$ 在直线 $l$ 上,且使 $PA + PB$ 最短,
点 $P$ 为 $A$ 和 $B^{\prime}$ 连线与直线 $l$ 的交点,
点 $P$ 的坐标为 $(0, 2)$。
用正方格纸中割补法:
完整方格为:$3×3=9$,
三角形外多算小三角形面积:$1+1.5+2=4.5$,
$\bigtriangleup ABC$面积= $ 4 × 3 - \frac{1}{2} × 1 × 3 - \frac{1}{2} × 2 × 3 - \frac{1}{2} × 1 × 2 - 1$,
即$12 - 1.5 - 3 - 1 - 1 = 5 - 0.5= 5$。
或直接计算:
$\bigtriangleup ABC面积 = \frac{1}{2} × 底 × 高 = \frac{1}{2} × 2 × 3 - 1× 2= 5 - (补上计算多余部分)= 5$。
答案为:$5$。
(2)
$A^{\prime} (2, 4)$,
$B^{\prime} (-1, 1)$,
$C^{\prime} (2, 2)$。
(3)
点 $P$ 在直线 $l$ 上,且使 $PA + PB$ 最短,
点 $P$ 为 $A$ 和 $B^{\prime}$ 连线与直线 $l$ 的交点,
点 $P$ 的坐标为 $(0, 2)$。
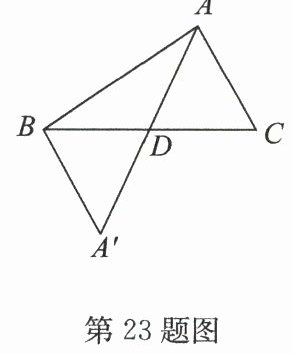
23. (8分)(2025·天宁区期中)如图,在△ABC中,D是BC边的中点,△A'BD与△ACD关于点D成中心对称.
(1)直接写出图中所有相等的线段;
(2)若∠BAC=85°,求∠A'BA的度数;
(3)若BC=10cm,AC=6cm,AA'=11cm,求△ACD的周长.
(1)直接写出图中所有相等的线段;
(2)若∠BAC=85°,求∠A'BA的度数;
(3)若BC=10cm,AC=6cm,AA'=11cm,求△ACD的周长.

答案:(1) AD=A'D,AC=A'B,BD=CD。
(2) ∵△A'BD与△ACD关于点D成中心对称,∴AD=A'D,BD=CD,∴四边形ABA'C是平行四边形,∴AC//A'B,∴∠BAC+∠A'BA=180°,∵∠BAC=85°,∴∠A'BA=180°-85°=95°。
(3) ∵D是BC中点,BC=10cm,∴CD=BC/2=5cm。∵△A'BD与△ACD关于点D成中心对称,∴AD=A'D,∵AA'=11cm,∴AD=AA'/2=5.5cm。△ACD的周长=AC+CD+AD=6+5+5.5=16.5cm。
(2) ∵△A'BD与△ACD关于点D成中心对称,∴AD=A'D,BD=CD,∴四边形ABA'C是平行四边形,∴AC//A'B,∴∠BAC+∠A'BA=180°,∵∠BAC=85°,∴∠A'BA=180°-85°=95°。
(3) ∵D是BC中点,BC=10cm,∴CD=BC/2=5cm。∵△A'BD与△ACD关于点D成中心对称,∴AD=A'D,∵AA'=11cm,∴AD=AA'/2=5.5cm。△ACD的周长=AC+CD+AD=6+5+5.5=16.5cm。
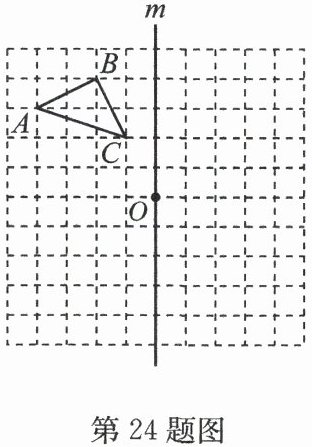
24. (8分)(2024·淮北中学月考)在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC绕点C顺时针旋转90°得到的△A₁B₁C;
(2)在网格中画出△ABC关于直线m对称的△A₂B₂C₂;
(3)在网格中画出△ABC绕点O顺时针旋转180°得到的△A₃B₃C₃;
(4)在网格中画出△ABC向下平移6个单位长度再向左平移1个单位长度得到的△A₄B₄C₄.
(1)在网格中画出△ABC绕点C顺时针旋转90°得到的△A₁B₁C;
(2)在网格中画出△ABC关于直线m对称的△A₂B₂C₂;
(3)在网格中画出△ABC绕点O顺时针旋转180°得到的△A₃B₃C₃;
(4)在网格中画出△ABC向下平移6个单位长度再向左平移1个单位长度得到的△A₄B₄C₄.

答案:(1)
绕点$C$顺时针旋转$90°$,$A$点坐标变化为:$A$相对于$C$的坐标为$(-1, 1)$,顺时针旋转$90°$后,坐标为$(1, 1)$,因此$A_1$的坐标为$C$的坐标加上$(1, 1)$,即$A_1$在$(0, 0)$基础上变化为$(1, -1)$(相对坐标变换后加上$C$的坐标$(1, 1)$,实际$A_1$为$(2, 1)$的网格点,通过图形直接确定$A_1$、$B_1$位置,画出$△ A_1B_1C$。
同理确定$B$绕$C$顺时针旋转$90°$后的$B_1$位置。
画出$△ A_1B_1C$。
(2)
关于直线$m$对称,$A$点对称后$A_2$位置根据对称轴$m$确定,$B$点对称后$B_2$位置确定,$C$点在对称轴上,位置不变。
画出$△ A_2B_2C_2$。
(3)
绕点$O$顺时针旋转$180°$,$A$点坐标$(x,y)$变为$(-x, -y)$,同理确定$B$、$C$旋转后$A_3$、$B_3$、$C_3$位置($C$绕$O$旋转$180°$后位置改变)。
画出$△ A_3B_3C_3$。
(4)
向下平移$6$个单位长度,$A$点纵坐标减$6$,$B$、$C$同理;再向左平移$1$个单位长度,$A$、$B$、$C$横坐标减$1$,确定$A_4$、$B_4$、$C_4$位置。
画出$△ A_4B_4C_4$。
图形答案依据网格准确画出对应图形(由于无法实际画图,以文字说明绘图方法,实际答题需在网格中准确绘制)。
绕点$C$顺时针旋转$90°$,$A$点坐标变化为:$A$相对于$C$的坐标为$(-1, 1)$,顺时针旋转$90°$后,坐标为$(1, 1)$,因此$A_1$的坐标为$C$的坐标加上$(1, 1)$,即$A_1$在$(0, 0)$基础上变化为$(1, -1)$(相对坐标变换后加上$C$的坐标$(1, 1)$,实际$A_1$为$(2, 1)$的网格点,通过图形直接确定$A_1$、$B_1$位置,画出$△ A_1B_1C$。
同理确定$B$绕$C$顺时针旋转$90°$后的$B_1$位置。
画出$△ A_1B_1C$。
(2)
关于直线$m$对称,$A$点对称后$A_2$位置根据对称轴$m$确定,$B$点对称后$B_2$位置确定,$C$点在对称轴上,位置不变。
画出$△ A_2B_2C_2$。
(3)
绕点$O$顺时针旋转$180°$,$A$点坐标$(x,y)$变为$(-x, -y)$,同理确定$B$、$C$旋转后$A_3$、$B_3$、$C_3$位置($C$绕$O$旋转$180°$后位置改变)。
画出$△ A_3B_3C_3$。
(4)
向下平移$6$个单位长度,$A$点纵坐标减$6$,$B$、$C$同理;再向左平移$1$个单位长度,$A$、$B$、$C$横坐标减$1$,确定$A_4$、$B_4$、$C_4$位置。
画出$△ A_4B_4C_4$。
图形答案依据网格准确画出对应图形(由于无法实际画图,以文字说明绘图方法,实际答题需在网格中准确绘制)。