8. (2024·南京)某商场促销方案规定:单笔消费金额每满 100 元立减 10 元. 例如,单笔消费金额为 208 元时,立减 20 元. 甲在该商场单笔购买 2 件 A 商品,立减了 20 元;乙在该商场单笔购买 2 件 A 商品与 1 件 B 商品,立减了 30 元. 若 B 商品的单价是整数元,则它的最小值是(
A.1 元
B.99 元
C.101 元
D.199 元
A
)A.1 元
B.99 元
C.101 元
D.199 元
答案:8. A
解析:
设A商品单价为$x$元,B商品单价为$y$元。
由甲购买2件A商品立减20元,得:$200 ≤ 2x < 300$,即$100 ≤ x < 150$。
由乙购买2件A商品与1件B商品立减30元,得:$300 ≤ 2x + y < 400$。
因为$100 ≤ x < 150$,所以$200 ≤ 2x < 300$,则$300 - 2x ≤ y < 400 - 2x$。
当$x$取最大值接近150时,$2x$接近300,$y$的最小值接近$300 - 300 = 0$,又因$y$为正整数,所以$y$最小值为1元。
A
由甲购买2件A商品立减20元,得:$200 ≤ 2x < 300$,即$100 ≤ x < 150$。
由乙购买2件A商品与1件B商品立减30元,得:$300 ≤ 2x + y < 400$。
因为$100 ≤ x < 150$,所以$200 ≤ 2x < 300$,则$300 - 2x ≤ y < 400 - 2x$。
当$x$取最大值接近150时,$2x$接近300,$y$的最小值接近$300 - 300 = 0$,又因$y$为正整数,所以$y$最小值为1元。
A
9. 用不等式表示“$x$与$a$的平方差不是正数”为
$x^{2}-a^{2}≤0$
.答案:9. $x^{2}-a^{2}≤0$
10. (新趋势·结论开放)(2025·宿豫区期末)写出一个解集如图所示的不等式组:.
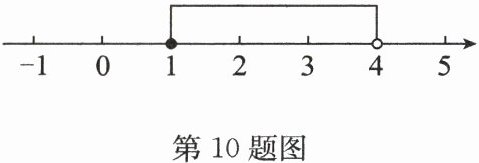

答案:10. $ \begin{cases}x - 1≥0, \\ x - 4<0\end{cases} $(答案不唯一)
解析:
$\begin{cases}x - 1≥0 \\ x - 4 < 0\end{cases}$
11. 不等式$\frac{1 + x}{2} ≥ \frac{2x + 1}{3}$的非负整数解为
0,1
.答案:11. 0,1
解析:
解:去分母,得$3(1 + x) ≥ 2(2x + 1)$
去括号,得$3 + 3x ≥ 4x + 2$
移项,得$3x - 4x ≥ 2 - 3$
合并同类项,得$-x ≥ -1$
系数化为1,得$x ≤ 1$
所以不等式的非负整数解为0,1
去括号,得$3 + 3x ≥ 4x + 2$
移项,得$3x - 4x ≥ 2 - 3$
合并同类项,得$-x ≥ -1$
系数化为1,得$x ≤ 1$
所以不等式的非负整数解为0,1
12. 若$2 < 2x - 2 < 10$,则$x$的取值范围是
$ 2< x<6 $
.答案:12. $ 2< x<6 $
解析:
解:$2 < 2x - 2 < 10$
$2 + 2 < 2x < 10 + 2$
$4 < 2x < 12$
$2 < x < 6$
$2 + 2 < 2x < 10 + 2$
$4 < 2x < 12$
$2 < x < 6$
13. (2024·如东区期末)不等式$\frac{3x - 1}{5} - \frac{x - 1}{2} ≥ 1$的最小整数解是
7
.答案:13. 7
解析:
去分母,得:$2(3x - 1) - 5(x - 1) ≥ 10$
去括号,得:$6x - 2 - 5x + 5 ≥ 10$
移项,得:$6x - 5x ≥ 10 + 2 - 5$
合并同类项,得:$x ≥ 7$
最小整数解是7
去括号,得:$6x - 2 - 5x + 5 ≥ 10$
移项,得:$6x - 5x ≥ 10 + 2 - 5$
合并同类项,得:$x ≥ 7$
最小整数解是7
14. (2024·丹徒区期末)三个连续正整数的和不大于 33,这样的正整数有
10
组.答案:14. 10
解析:
设三个连续正整数分别为$n$,$n + 1$,$n + 2$($n$为正整数)。
由题意得:$n + (n + 1) + (n + 2) ≤ 33$
化简得:$3n + 3 ≤ 33$
$3n ≤ 30$
$n ≤ 10$
因为$n$为正整数,所以$n$可取$1,2,3,···,10$,共10个值。
10
由题意得:$n + (n + 1) + (n + 2) ≤ 33$
化简得:$3n + 3 ≤ 33$
$3n ≤ 30$
$n ≤ 10$
因为$n$为正整数,所以$n$可取$1,2,3,···,10$,共10个值。
10
15. (2025·金坛区期末)如果关于$x$的不等式组$\begin{cases}\frac{x + 3}{2} ≥ x - 1, \\ 3x + 6 > a + 4\end{cases}$有且只有 5 个整数解,那么符合条件的所有整数$a$的和为 ______ .
答案:15. 9
解析:
解不等式组:
1. 解$\frac{x + 3}{2} ≥ x - 1$,得$x + 3 ≥ 2x - 2$,$x ≤ 5$。
2. 解$3x + 6 > a + 4$,得$3x > a - 2$,$x > \frac{a - 2}{3}$。
不等式组的解集为$\frac{a - 2}{3} < x ≤ 5$。
整数解为5,4,3,2,1,共5个,所以$0 ≤ \frac{a - 2}{3} < 1$。
解得$2 ≤ a < 5$,整数$a$为2,3,4。
和为$2 + 3 + 4 = 9$。
9
1. 解$\frac{x + 3}{2} ≥ x - 1$,得$x + 3 ≥ 2x - 2$,$x ≤ 5$。
2. 解$3x + 6 > a + 4$,得$3x > a - 2$,$x > \frac{a - 2}{3}$。
不等式组的解集为$\frac{a - 2}{3} < x ≤ 5$。
整数解为5,4,3,2,1,共5个,所以$0 ≤ \frac{a - 2}{3} < 1$。
解得$2 ≤ a < 5$,整数$a$为2,3,4。
和为$2 + 3 + 4 = 9$。
9
16. 现用甲、乙两种汽车将 46 吨防洪物资运往灾区,甲种汽车载重 5 吨,乙种汽车载重 4 吨. 若一共安排 10 辆汽车运送这些物资,则甲种汽车至少应安排
6
辆.答案:16. 6
解析:
设甲种汽车安排$x$辆,则乙种汽车安排$(10 - x)$辆。
根据题意,得$5x + 4(10 - x) ≥ 46$
$5x + 40 - 4x ≥ 46$
$x ≥ 6$
甲种汽车至少应安排$6$辆。
根据题意,得$5x + 4(10 - x) ≥ 46$
$5x + 40 - 4x ≥ 46$
$x ≥ 6$
甲种汽车至少应安排$6$辆。
17. 用若干辆载重量为 6 吨的货车运一批货物,若每辆汽车只装 4 吨货物,则剩下 18 吨货物;若每辆汽车装 6 吨货物,则最后一辆货车装的货物不足 5 吨. 若设有$x$辆货车,则$x$应满足的不等式组是.
答案:17. $ \begin{cases}4x + 18 - 6(x - 1)<5, \\ 4x + 18 - 6(x - 1)≥0\end{cases} $
18. 对于有理数$a$,$b$,定义运算“※”为$a※b = a + 3b$. 例如$5※2 = 5 + 3×2 = 11$,则关于$x$的不等式$x※m < 2$有且只有一个正整数解时,$m$的取值范围是
$ 0≤ m<\frac{1}{3} $
.答案:18. $ 0≤ m<\frac{1}{3} $
解析:
解:由定义知$x※m = x + 3m$,则不等式为$x + 3m < 2$,解得$x < 2 - 3m$。
因为不等式有且只有一个正整数解,正整数解只能为$1$,所以$1 < 2 - 3m ≤ 2$。
解$1 < 2 - 3m$得$3m < 1$,即$m < \frac{1}{3}$;
解$2 - 3m ≤ 2$得$-3m ≤ 0$,即$m ≥ 0$。
综上,$0 ≤ m < \frac{1}{3}$。
$0≤ m<\frac{1}{3}$
因为不等式有且只有一个正整数解,正整数解只能为$1$,所以$1 < 2 - 3m ≤ 2$。
解$1 < 2 - 3m$得$3m < 1$,即$m < \frac{1}{3}$;
解$2 - 3m ≤ 2$得$-3m ≤ 0$,即$m ≥ 0$。
综上,$0 ≤ m < \frac{1}{3}$。
$0≤ m<\frac{1}{3}$
19. (8 分)解下列不等式(组):
(1)$1 - \frac{x + 6}{2} < \frac{2x + 1}{3}$;
(2)$\begin{cases}x - 1 < 0, \\ \frac{5x + 1}{2} ≥ x - 1.\end{cases}$
(1)$1 - \frac{x + 6}{2} < \frac{2x + 1}{3}$;
(2)$\begin{cases}x - 1 < 0, \\ \frac{5x + 1}{2} ≥ x - 1.\end{cases}$
答案:19. 解:(1)去分母,得 $ 6 - 3(x + 6)<2(2x + 1) $,
去括号,得 $ 6 - 3x - 18<4x + 2 $,
移项,得 $ - 3x - 4x<2 - 6 + 18 $,
合并同类项,得 $ - 7x<14 $,
两边都除以 - 7,得 $ x> - 2 $。
(2)$ \begin{cases}x - 1<0,① \\ \frac{5x + 1}{2}≥ x - 1,②\end{cases} $
解不等式①,得 $ x<1 $,
解不等式②,得 $ x≥ - 1 $,
所以原不等式组的解集为 $ - 1≤ x<1 $。
去括号,得 $ 6 - 3x - 18<4x + 2 $,
移项,得 $ - 3x - 4x<2 - 6 + 18 $,
合并同类项,得 $ - 7x<14 $,
两边都除以 - 7,得 $ x> - 2 $。
(2)$ \begin{cases}x - 1<0,① \\ \frac{5x + 1}{2}≥ x - 1,②\end{cases} $
解不等式①,得 $ x<1 $,
解不等式②,得 $ x≥ - 1 $,
所以原不等式组的解集为 $ - 1≤ x<1 $。