20. (6 分)求不等式$- 3 < 4x - 7 ≤ 9$的整数解.
答案:20. 解:因为 $ - 3<4x - 7≤9 $,
所以 $ - 3 + 7<4x - 7 + 7≤9 + 7 $,即 $ 4<4x≤16 $,
所以 $ 1< x≤4 $。
所以原不等式的解集为 $ 1< x≤4 $,其整数解为 2,3,4。
所以 $ - 3 + 7<4x - 7 + 7≤9 + 7 $,即 $ 4<4x≤16 $,
所以 $ 1< x≤4 $。
所以原不等式的解集为 $ 1< x≤4 $,其整数解为 2,3,4。
21. (6 分)(2024·眉山)解不等式:$\frac{x + 1}{3} - 1 ≤ \frac{2 - x}{2}$,把它的解集表示在如图所示的数轴上.


答案:
21. 解:去分母,得 $ 2(x + 1) - 6≤3(2 - x) $,
去括号,得 $ 2x + 2 - 6≤6 - 3x $,
移项,得 $ 2x + 3x≤6 + 6 - 2 $,
合并同类项,得 $ 5x≤10 $,
两边都除以 5,得 $ x≤2 $,
所以原不等式的解集为 $ x≤2 $,在数轴上表示如答图。

21. 解:去分母,得 $ 2(x + 1) - 6≤3(2 - x) $,
去括号,得 $ 2x + 2 - 6≤6 - 3x $,
移项,得 $ 2x + 3x≤6 + 6 - 2 $,
合并同类项,得 $ 5x≤10 $,
两边都除以 5,得 $ x≤2 $,
所以原不等式的解集为 $ x≤2 $,在数轴上表示如答图。

22. (6 分)(2024·天津)解不等式组$\begin{cases}2x + 1 ≤ 3,① \\ 3x - 1 ≥ x - 7.②\end{cases}$
请结合题意填空,完成本题的解答.
(1)解不等式①,得
(2)解不等式②,得
(3)把不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为
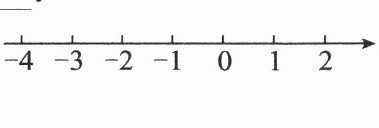
请结合题意填空,完成本题的解答.
(1)解不等式①,得
$ x≤1 $
;(2)解不等式②,得
$ x≥ - 3 $
;(3)把不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为
$ - 3≤ x≤1 $
.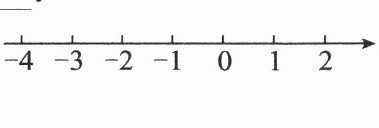
答案:
22. (1)$ x≤1 $ (2)$ x≥ - 3 $
(3)解:解集在数轴上表示如答图。
(4)$ - 3≤ x≤1 $

22. (1)$ x≤1 $ (2)$ x≥ - 3 $
(3)解:解集在数轴上表示如答图。
(4)$ - 3≤ x≤1 $

23. (6 分)关于$x$,$y$的方程组$\begin{cases}x + 3y = 3 - 2k, \\ 3x + y = 1 + k\end{cases}$的解满足$x + y > 0$,且关于$x$的不等式组$\begin{cases}x - 2(x - 1) ≤ 3, \\ \frac{2k + x}{3} ≥ x\end{cases}$有解,求所有符合条件的整数$k$的值的和.
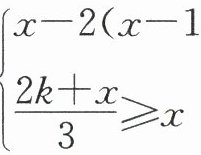
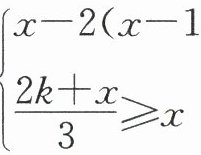
答案:23. 解:$ \begin{cases}x + 3y = 3 - 2k,① \\ 3x + y = 1 + k,②\end{cases} $
① + ②,得 $ 4x + 4y = 4 - k $,所以 $ x + y = 1 - \frac{1}{4}k $。
因为 $ x + y>0 $,所以 $ 1 - \frac{1}{4}k>0 $,解得 $ k<4 $。
$ \begin{cases}x - 2(x - 1)≤3,③ \\ \frac{2k + x}{3}≥ x,④\end{cases} $
解不等式③,得 $ x≥ - 1 $,
解不等式④,得 $ x≤ k $。
因为关于 $ x $ 的不等式组 $ \begin{cases}x - 2(x - 1)≤3, \\ \frac{2k + x}{3}≥ x\end{cases} $ 有解,
所以 $ k≥ - 1 $,
综上可得,$ - 1≤ k<4 $,
所以符合条件的整数 $ k $ 的值的和为 $ - 1 + 0 + 1 + 2 + 3 = 5 $。
① + ②,得 $ 4x + 4y = 4 - k $,所以 $ x + y = 1 - \frac{1}{4}k $。
因为 $ x + y>0 $,所以 $ 1 - \frac{1}{4}k>0 $,解得 $ k<4 $。
$ \begin{cases}x - 2(x - 1)≤3,③ \\ \frac{2k + x}{3}≥ x,④\end{cases} $
解不等式③,得 $ x≥ - 1 $,
解不等式④,得 $ x≤ k $。
因为关于 $ x $ 的不等式组 $ \begin{cases}x - 2(x - 1)≤3, \\ \frac{2k + x}{3}≥ x\end{cases} $ 有解,
所以 $ k≥ - 1 $,
综上可得,$ - 1≤ k<4 $,
所以符合条件的整数 $ k $ 的值的和为 $ - 1 + 0 + 1 + 2 + 3 = 5 $。
24. (6 分)已知关于$x$,$y$的方程组$\begin{cases}x - y = m + 6, \\ x + y = 3m + 2\end{cases}$的解满足$x ≥ 0$,$y < 0$.
(1)求$m$的取值范围;
(2)在$m$的取值范围内,当$m$取何整数时,不等式$(2m + 1)x < 2m + 1$的解集为$x > 1$?
(1)求$m$的取值范围;
(2)在$m$的取值范围内,当$m$取何整数时,不等式$(2m + 1)x < 2m + 1$的解集为$x > 1$?
答案:24. 解:(1)$ \begin{cases}x - y = m + 6,① \\ x + y = 3m + 2,②\end{cases} $
① + ②,得 $ 2x = 4m + 8 $,解得 $ x = 2m + 4 $。
② - ①,得 $ 2y = 2m - 4 $,解得 $ y = m - 2 $,
故原方程组的解为 $ \begin{cases}x = 2m + 4, \\ y = m - 2.\end{cases} $
因为方程组 $ \begin{cases}x - y = m + 6, \\ x + y = 3m + 2\end{cases} $ 的解满足 $ x≥0 $,$ y<0 $,
所以 $ \begin{cases}2m + 4≥0, \\ m - 2<0,\end{cases} $ 解得 $ - 2≤ m<2 $。
所以 $ m $ 的取值范围是 $ - 2≤ m<2 $。
(2)因为不等式 $ (2m + 1)x<2m + 1 $ 的解集为 $ x>1 $,
所以 $ 2m + 1<0 $,即 $ m< - \frac{1}{2} $。
又因为 $ - 2≤ m<2 $,所以 $ - 2≤ m< - \frac{1}{2} $。
又因为 $ m $ 是整数,所以 $ m $ 的值是 - 2 或 - 1。
① + ②,得 $ 2x = 4m + 8 $,解得 $ x = 2m + 4 $。
② - ①,得 $ 2y = 2m - 4 $,解得 $ y = m - 2 $,
故原方程组的解为 $ \begin{cases}x = 2m + 4, \\ y = m - 2.\end{cases} $
因为方程组 $ \begin{cases}x - y = m + 6, \\ x + y = 3m + 2\end{cases} $ 的解满足 $ x≥0 $,$ y<0 $,
所以 $ \begin{cases}2m + 4≥0, \\ m - 2<0,\end{cases} $ 解得 $ - 2≤ m<2 $。
所以 $ m $ 的取值范围是 $ - 2≤ m<2 $。
(2)因为不等式 $ (2m + 1)x<2m + 1 $ 的解集为 $ x>1 $,
所以 $ 2m + 1<0 $,即 $ m< - \frac{1}{2} $。
又因为 $ - 2≤ m<2 $,所以 $ - 2≤ m< - \frac{1}{2} $。
又因为 $ m $ 是整数,所以 $ m $ 的值是 - 2 或 - 1。