1.(2025·姑苏区期末)下列语句:①正整数和负整数都是整数;②含有未知数的等式叫作方程;③对顶角相等;④在同一平面内,不相交的两条直线叫作平行线. 其中属于定义的是(
A.①②
B.①③
C.②④
D.①②③④
C
)A.①②
B.①③
C.②④
D.①②③④
答案:1.C
2. 下列命题中,是真命题的是(
A.同位角相等
B.0 没有相反数
C.若 $ a^{2}=b^{2} $,则 $ a = b $
D.等角的余角相等
D
)A.同位角相等
B.0 没有相反数
C.若 $ a^{2}=b^{2} $,则 $ a = b $
D.等角的余角相等
答案:2.D
3.(2025·宿豫区期中)六边形的外角和是(
A.$ 1080^{\circ} $
B.$ 720^{\circ} $
C.$ 360^{\circ} $
D.$ 180^{\circ} $
C
)A.$ 1080^{\circ} $
B.$ 720^{\circ} $
C.$ 360^{\circ} $
D.$ 180^{\circ} $
答案:3.C
4. 用反证法证明命题“等腰三角形的底角是锐角”时,第一步应假设(
A.等腰三角形的底角是直角或钝角
B.等腰三角形的底角是直角
C.等腰三角形的底角是钝角
D.等腰三角形的底角是锐角
A
)A.等腰三角形的底角是直角或钝角
B.等腰三角形的底角是直角
C.等腰三角形的底角是钝角
D.等腰三角形的底角是锐角
答案:4.A
5.(2024·经开区期末)在$ △ ABC $中,满足下列条件:①$ ∠ A = 60^{\circ} $,$ ∠ C = 30^{\circ} $;②$ ∠ A - ∠ B = ∠ C $;③$ ∠ A:∠ B:∠ C = 3:4:5 $;④$ ∠ A + ∠ C = 90^{\circ} $. 能确定$ △ ABC $是直角三角形的有(
A.1 个
B.2 个
C.3 个
D.4 个
C
)A.1 个
B.2 个
C.3 个
D.4 个
答案:5.C
解析:
①在△ABC中,∠A=60°,∠C=30°,则∠B=180°-∠A-∠C=180°-60°-30°=90°,是直角三角形;
②∠A-∠B=∠C,又∠A+∠B+∠C=180°,则∠A-∠B+∠A+∠B=180°,2∠A=180°,∠A=90°,是直角三角形;
③∠A:∠B:∠C=3:4:5,设∠A=3x,∠B=4x,∠C=5x,3x+4x+5x=180°,12x=180°,x=15°,∠C=5×15°=75°,不是直角三角形;
④∠A+∠C=90°,则∠B=180°-(∠A+∠C)=90°,是直角三角形。
能确定△ABC是直角三角形的有①②④,共3个。
C
②∠A-∠B=∠C,又∠A+∠B+∠C=180°,则∠A-∠B+∠A+∠B=180°,2∠A=180°,∠A=90°,是直角三角形;
③∠A:∠B:∠C=3:4:5,设∠A=3x,∠B=4x,∠C=5x,3x+4x+5x=180°,12x=180°,x=15°,∠C=5×15°=75°,不是直角三角形;
④∠A+∠C=90°,则∠B=180°-(∠A+∠C)=90°,是直角三角形。
能确定△ABC是直角三角形的有①②④,共3个。
C
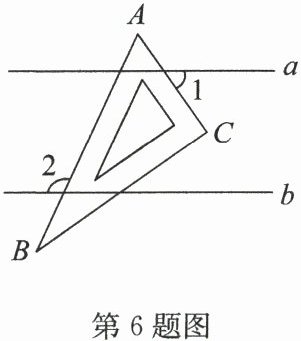
6.(2024·宿豫区期末)如图,直线 $ a // b $,一块含 $ 60^{\circ} $角的直角三角尺 $ ABC(∠ A = 60^{\circ}) $按如图所示放置. 若 $ ∠ 1 = 55^{\circ} $,则 $ ∠ 2 $的度数为(
A.$ 105^{\circ} $
B.$ 110^{\circ} $
C.$ 115^{\circ} $
D.$ 120^{\circ} $
C
)
A.$ 105^{\circ} $
B.$ 110^{\circ} $
C.$ 115^{\circ} $
D.$ 120^{\circ} $
答案:6.C
解析:
解:设三角尺的直角顶点为$D$(图中未标出,假设为$AC$与直线$a$的交点),延长$BC$交直线$b$于点$E$。
因为直线$a// b$,所以$∠ 1$的同位角(设为$∠ AED$)等于$∠ 1 = 55^{\circ}$。
在$△ ADE$中,$∠ A = 60^{\circ}$,$∠ AED = 55^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$∠ ADE = 180^{\circ} - 60^{\circ} - 55^{\circ} = 65^{\circ}$。
因为$∠ ADE$与$∠ 2$互补(平角定义),所以$∠ 2 = 180^{\circ} - 65^{\circ} = 115^{\circ}$。
答案:C
因为直线$a// b$,所以$∠ 1$的同位角(设为$∠ AED$)等于$∠ 1 = 55^{\circ}$。
在$△ ADE$中,$∠ A = 60^{\circ}$,$∠ AED = 55^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$∠ ADE = 180^{\circ} - 60^{\circ} - 55^{\circ} = 65^{\circ}$。
因为$∠ ADE$与$∠ 2$互补(平角定义),所以$∠ 2 = 180^{\circ} - 65^{\circ} = 115^{\circ}$。
答案:C
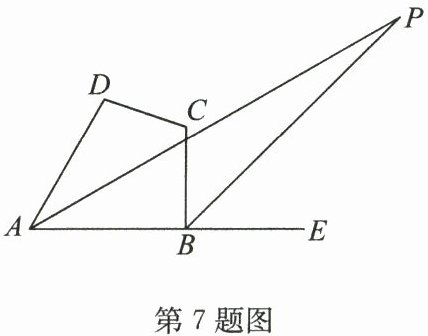
7. 如图,在四边形 $ ABCD $中,$ ∠ DAB $的平分线与$ ∠ ABC $的外角平分线相交于点 $ P $,且$ ∠ D + ∠ C = 210^{\circ} $,则$ ∠ P = $(
A.$ 10^{\circ} $
B.$ 15^{\circ} $
C.$ 30^{\circ} $
D.$ 40^{\circ} $
B
)
A.$ 10^{\circ} $
B.$ 15^{\circ} $
C.$ 30^{\circ} $
D.$ 40^{\circ} $
答案:7.B
解析:
解:在四边形$ABCD$中,$∠ DAB + ∠ ABC + ∠ C + ∠ D = 360^{\circ}$,
$\because ∠ D + ∠ C = 210^{\circ}$,
$\therefore ∠ DAB + ∠ ABC = 360^{\circ} - 210^{\circ} = 150^{\circ}$。
$\because AP$平分$∠ DAB$,$BP$平分$∠ ABC$的外角,
$\therefore ∠ PAB = \frac{1}{2}∠ DAB$,$∠ PBE = \frac{1}{2}(180^{\circ} - ∠ ABC)$。
在$△ ABP$中,$∠ P + ∠ PAB = ∠ PBE$,
$\therefore ∠ P = ∠ PBE - ∠ PAB = \frac{1}{2}(180^{\circ} - ∠ ABC) - \frac{1}{2}∠ DAB$
$= 90^{\circ} - \frac{1}{2}(∠ ABC + ∠ DAB) = 90^{\circ} - \frac{1}{2} × 150^{\circ} = 15^{\circ}$。
答案:B
$\because ∠ D + ∠ C = 210^{\circ}$,
$\therefore ∠ DAB + ∠ ABC = 360^{\circ} - 210^{\circ} = 150^{\circ}$。
$\because AP$平分$∠ DAB$,$BP$平分$∠ ABC$的外角,
$\therefore ∠ PAB = \frac{1}{2}∠ DAB$,$∠ PBE = \frac{1}{2}(180^{\circ} - ∠ ABC)$。
在$△ ABP$中,$∠ P + ∠ PAB = ∠ PBE$,
$\therefore ∠ P = ∠ PBE - ∠ PAB = \frac{1}{2}(180^{\circ} - ∠ ABC) - \frac{1}{2}∠ DAB$
$= 90^{\circ} - \frac{1}{2}(∠ ABC + ∠ DAB) = 90^{\circ} - \frac{1}{2} × 150^{\circ} = 15^{\circ}$。
答案:B
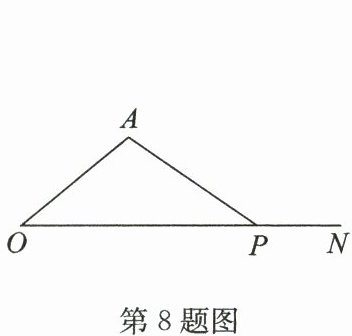
8.(2025·宿豫区期中)如图,$ P $是射线 $ ON $上一动点(不与点 $ O $重合),$ ∠ O = 40^{\circ} $. 若$ △ AOP $是钝角三角形,则$ ∠ A $的取值范围是(
A.$ 0^{\circ} < ∠ A < 50^{\circ} $
B.$ 90^{\circ} < ∠ A < 180^{\circ} $
C.$ 0^{\circ} < ∠ A < 40^{\circ} $或 $ 90^{\circ} < ∠ A < 140^{\circ} $
D.$ 0^{\circ} < ∠ A < 50^{\circ} $或 $ 90^{\circ} < ∠ A < 140^{\circ} $
D
)
A.$ 0^{\circ} < ∠ A < 50^{\circ} $
B.$ 90^{\circ} < ∠ A < 180^{\circ} $
C.$ 0^{\circ} < ∠ A < 40^{\circ} $或 $ 90^{\circ} < ∠ A < 140^{\circ} $
D.$ 0^{\circ} < ∠ A < 50^{\circ} $或 $ 90^{\circ} < ∠ A < 140^{\circ} $
答案:8.D
解析:
解:在△AOP中,∠O=40°,∠A+∠O+∠APO=180°,则∠A+∠APO=140°。
情况1:∠O为锐角,∠A为钝角
∠A>90°,且∠APO=140°-∠A>0°,
∴90°<∠A<140°。
情况2:∠O为锐角,∠APO为钝角
∠APO>90°,则∠A=140°-∠APO<50°,
又∠A>0°,
∴0°<∠A<50°。
综上,∠A的取值范围是0°<∠A<50°或90°<∠A<140°。
答案:D
情况1:∠O为锐角,∠A为钝角
∠A>90°,且∠APO=140°-∠A>0°,
∴90°<∠A<140°。
情况2:∠O为锐角,∠APO为钝角
∠APO>90°,则∠A=140°-∠APO<50°,
又∠A>0°,
∴0°<∠A<50°。
综上,∠A的取值范围是0°<∠A<50°或90°<∠A<140°。
答案:D