9. 下列语句:①水仙属多年生草本植物;②对顶角相等;③一个数的绝对值一定是非负数吗?④直角都相等;⑤圆的面积;⑥$ ∠ AOB = 90^{\circ} $. 其中属于命题的是
①②④
.(填序号)答案:9.①②④
10. 把“二元一次方程是整式方程”改写成“如果……,那么……”的形式为
如果一个方程是二元一次方程,那么这个方程是整式方程
.答案:10.如果一个方程是二元一次方程,那么这个方程是整式方程
11. 给“非负数”下的定义为
大于或等于0的数叫作非负数
.答案:11.大于或等于0的数叫作非负数
12.(2025·宿豫区期末)命题“在数轴上,表示互为相反数的两个数的点到原点的距离相等”的逆命题是
在数轴上,到原点的距离相等的两个点表示的数互为相反数
.答案:12.在数轴上,到原点的距离相等的两个点表示的数互为相反数
13. 有下列说法:①若 $ a $与 $ b $互为相反数,则 $ a + b = 0 $;②若 $ ab = 1 $,则 $ a $与 $ b $互为倒数;③两点之间,直线最短;④若$ ∠ α + ∠ β = 90^{\circ} $,且$ ∠ β $与$ ∠ \gamma $互余,则$ ∠ α $与$ ∠ \gamma $互余;⑤若$ ∠ α $为锐角,且$ ∠ α $与$ ∠ β $互补,$ ∠ α $与$ ∠ \gamma $互余,则$ ∠ β - ∠ \gamma = 90^{\circ} $. 其中正确的有
①②⑤
.(填序号)答案:13.①②⑤
14. 一个零件的横截面是正八边形,每个内角都相等,则每个内角的度数是
135
$ ^{\circ} $.答案:14.135
解析:
正八边形的内角和为$(8 - 2)×180^{\circ}=1080^{\circ}$,每个内角的度数是$1080^{\circ}÷8 = 135^{\circ}$。
15. 如图,点 $ D $在$ △ ABC $的边 $ AC $的延长线上,$ BC // DE $. 若$ ∠ B = 32^{\circ} $,$ ∠ D = 72^{\circ} $,则$ ∠ A $的度数是
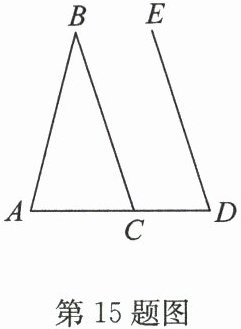
76°
.
答案:15.76°
16.(2025·宿城区期中)如图是一副三角尺拼成的图案,则$ ∠ AED $的度数为
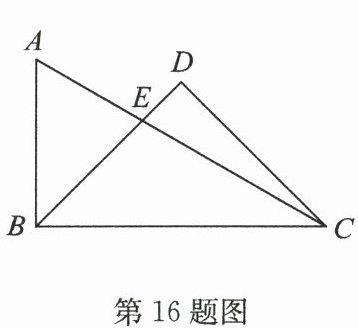
105°
.
答案:16.105°
解析:
解:在三角尺中,$∠ABC=90°$,$∠BAC=45°$,$∠DCE=30°$,$∠DEC=90°$。
在$△ ABC$中,$∠ACB=180°-∠BAC-∠ABC=180°-45°-90°=45°$。
$∠ECD=30°$,则$∠BCE=∠ACB - ∠ECD=45° - 30°=15°$。
在$△ BEC$中,$∠BEC=180°-∠EBC-∠BCE=180°-90°-15°=75°$。
$∠AED$与$∠BEC$是对顶角,所以$∠AED=∠BEC=75°$。
答案:$75°$
在$△ ABC$中,$∠ACB=180°-∠BAC-∠ABC=180°-45°-90°=45°$。
$∠ECD=30°$,则$∠BCE=∠ACB - ∠ECD=45° - 30°=15°$。
在$△ BEC$中,$∠BEC=180°-∠EBC-∠BCE=180°-90°-15°=75°$。
$∠AED$与$∠BEC$是对顶角,所以$∠AED=∠BEC=75°$。
答案:$75°$
17.(2025·宿城区期中)如图,一束平行太阳光线 $ FA $,$ GB $照射到各内角都相等的五边形 $ ABCDE $上. 若$ ∠ ABG = 50^{\circ} $,则$ ∠ FAE $的度数是
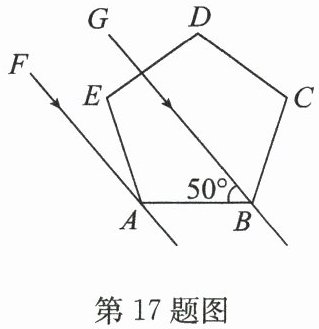
22
$ ^{\circ} $.
答案:17.22
解析:
解:五边形内角和为$(5 - 2)×180^{\circ} = 540^{\circ}$,各内角相等,故每个内角为$540^{\circ}÷5 = 108^{\circ}$,即$∠ABC = 108^{\circ}$。
因为$FA// GB$,所以$∠FAB + ∠ABG = 180^{\circ}$(两直线平行,同旁内角互补)。
已知$∠ABG = 50^{\circ}$,则$∠FAB = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
又因为$∠FAB = ∠FAE + ∠EAB$,且$∠EAB = 108^{\circ}$,所以$∠FAE = ∠FAB - ∠EAB = 130^{\circ} - 108^{\circ} = 22^{\circ}$。
22
因为$FA// GB$,所以$∠FAB + ∠ABG = 180^{\circ}$(两直线平行,同旁内角互补)。
已知$∠ABG = 50^{\circ}$,则$∠FAB = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
又因为$∠FAB = ∠FAE + ∠EAB$,且$∠EAB = 108^{\circ}$,所以$∠FAE = ∠FAB - ∠EAB = 130^{\circ} - 108^{\circ} = 22^{\circ}$。
22
18.(2024·达州)如图,在$ △ ABC $中,$ AE_{1} $,$ BE_{1} $分别是内角$ ∠ CAB $,外角$ ∠ CBD $的三等分线,且$ ∠ E_{1}AD = \frac{1}{3}∠ CAB $,$ ∠ E_{1}BD = \frac{1}{3}∠ CBD $;在$ △ ABE_{1} $中,$ AE_{2} $,$ BE_{2} $分别是内角$ ∠ E_{1}AB $,外角 $ E_{1}BD $的三等分线,且$ ∠ E_{2}AD = \frac{1}{3}∠ E_{1}AB $,$ ∠ E_{2}BD = \frac{1}{3}∠ E_{1}BD $,…,以此规律作下去. 若$ ∠ C = m^{\circ} $,则$ ∠ E_{n} = \_\_\_\_\_\_ ^{\circ} $.
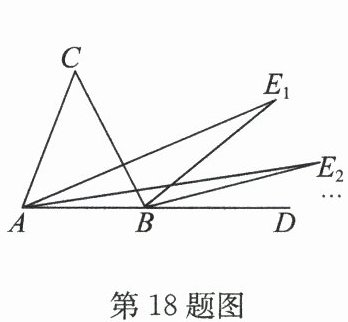

答案:18. $\frac{m}{3^{n}}$
解析:
证明:设$∠ CAB = 3α$,则$∠ E_{1}AD = α$,$∠ E_{1}AB = 3α - α = 2α$。
$∠ CBD$是$△ ABC$的外角,$∠ CBD = ∠ C + ∠ CAB = m^{\circ} + 3α$,$∠ E_{1}BD = \frac{1}{3}∠ CBD = \frac{m^{\circ} + 3α}{3} = \frac{m^{\circ}}{3} + α$。
在$△ ABE_{1}$中,$∠ E_{1}BD$是外角,$∠ E_{1}BD = ∠ E_{1}AB + ∠ E_{1}$,即$\frac{m^{\circ}}{3} + α = 2α + ∠ E_{1}$,解得$∠ E_{1} = \frac{m^{\circ}}{3}$。
同理,在$△ ABE_{1}$中,设$∠ E_{1}AB = 3β$,则$∠ E_{2}AD = β$,$∠ E_{2}AB = 3β - β = 2β$,$∠ E_{1}BD = 3\gamma$,$∠ E_{2}BD = \gamma$,可得$∠ E_{2} = \frac{∠ E_{1}}{3} = \frac{m^{\circ}}{3^{2}}$。
以此类推,$∠ E_{n} = \frac{m}{3^{n}}$。
$\frac{m}{3^{n}}$
$∠ CBD$是$△ ABC$的外角,$∠ CBD = ∠ C + ∠ CAB = m^{\circ} + 3α$,$∠ E_{1}BD = \frac{1}{3}∠ CBD = \frac{m^{\circ} + 3α}{3} = \frac{m^{\circ}}{3} + α$。
在$△ ABE_{1}$中,$∠ E_{1}BD$是外角,$∠ E_{1}BD = ∠ E_{1}AB + ∠ E_{1}$,即$\frac{m^{\circ}}{3} + α = 2α + ∠ E_{1}$,解得$∠ E_{1} = \frac{m^{\circ}}{3}$。
同理,在$△ ABE_{1}$中,设$∠ E_{1}AB = 3β$,则$∠ E_{2}AD = β$,$∠ E_{2}AB = 3β - β = 2β$,$∠ E_{1}BD = 3\gamma$,$∠ E_{2}BD = \gamma$,可得$∠ E_{2} = \frac{∠ E_{1}}{3} = \frac{m^{\circ}}{3^{2}}$。
以此类推,$∠ E_{n} = \frac{m}{3^{n}}$。
$\frac{m}{3^{n}}$
19.(6 分)写出下列命题的逆命题,并判断原命题与逆命题的真假.
(1)如果一个整数为偶数,那么它能被 2 整除;
(2)如果 $ x $满足 $ |x - 5| = 3 $,那么 $ x = 8 $.
(1)如果一个整数为偶数,那么它能被 2 整除;
(2)如果 $ x $满足 $ |x - 5| = 3 $,那么 $ x = 8 $.
答案:19.解:(1)逆命题:如果一个整数能被2整除,那么这个数是偶数.原命题是真命题,逆命题也是真命题.
(2)逆命题:如果x = 8,那么|x−5| = 3.原命题是假命题,逆命题是真命题.
(2)逆命题:如果x = 8,那么|x−5| = 3.原命题是假命题,逆命题是真命题.