20.(6 分)如图,点 $ C $,$ E $,$ B $,$ F $在一条直线上,$ AC // FD $,$ ∠ A = ∠ D $. 求证:$ AB // DE $.
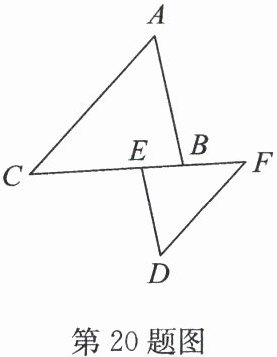

答案:20.证明:因为AC//FD,所以∠C = ∠F.
又因为∠A = ∠D,∠A + ∠C + ∠ABC = ∠D + ∠F + ∠DEF = 180°,
所以∠ABC = ∠DEF,所以AB//DE.
又因为∠A = ∠D,∠A + ∠C + ∠ABC = ∠D + ∠F + ∠DEF = 180°,
所以∠ABC = ∠DEF,所以AB//DE.
21.(6 分)小明同学观察下列式子:$ 3^{2} - 1^{2} = 8 $;$ 5^{2} - 3^{2} = 16 $;$ 7^{2} - 5^{2} = 24 $;$ 9^{2} - 7^{2} = 32 $;…;他发现了下面的结论:两个连续奇数的平方差一定是 8 的倍数. 请运用你所学过的知识,说明小明得到的结论是正确的.
答案:21.解:设两个连续的奇数为2n + 1,2n−1,n为整数.因为(2n + 1)²−(2n−1)² = 4n² + 4n + 1−(4n²−4n + 1)= 4n² + 4n + 1−4n² + 4n−1 = 8n(n为整数),所以两个连续奇数的平方差一定是8的倍数.
解析:
解:设两个连续的奇数为$2n + 1$,$2n - 1$,$n$为整数。
$\begin{aligned}(2n + 1)^2 - (2n - 1)^2&=4n^2 + 4n + 1 - (4n^2 - 4n + 1)\\&=4n^2 + 4n + 1 - 4n^2 + 4n - 1\\&=8n\end{aligned}$
因为$n$为整数,所以$8n$是$8$的倍数,即两个连续奇数的平方差一定是$8$的倍数。
$\begin{aligned}(2n + 1)^2 - (2n - 1)^2&=4n^2 + 4n + 1 - (4n^2 - 4n + 1)\\&=4n^2 + 4n + 1 - 4n^2 + 4n - 1\\&=8n\end{aligned}$
因为$n$为整数,所以$8n$是$8$的倍数,即两个连续奇数的平方差一定是$8$的倍数。
22.(6 分)根据命题“若两条平行线被第三条直线所截,则同旁内角的平分线互相垂直”,画出图形,写出已知、求证(不用证明).
答案:
22.解:已知:如答图,AB//CD,直线EF分别交AB,CD 于点G,H,GO平分∠BGF,HO平分∠DHE.
求证:OG⊥OH.
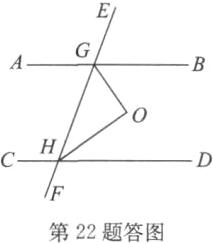
22.解:已知:如答图,AB//CD,直线EF分别交AB,CD 于点G,H,GO平分∠BGF,HO平分∠DHE.
求证:OG⊥OH.

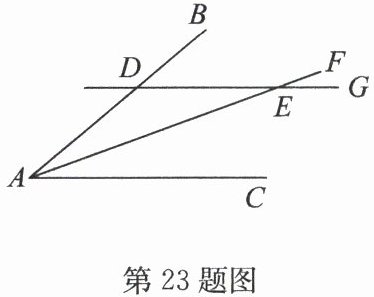
23.(6 分)(2024·宿豫区期末)如图,点 $ D $在 $ AB $上,直线 $ DG $交 $ AF $于点 $ E $. 请从①$ DG // AC $;②$ AF $平分$ ∠ BAC $;③$ ∠ DAE = ∠ DEA $中任选两个作为条件,余下一个作为结论,构造一个真命题,并求证.
已知:
证明:
已知:
①②
,求证:③
.(填序号)证明:

答案:23.解:(答案不唯一)
已知:①②,
求证:③.
证明:因为DG//AC,所以∠DEA = ∠EAC.
因为AF平分∠BAC,所以∠DAE = ∠EAC,
所以∠DAE = ∠DEA.
已知:①②,
求证:③.
证明:因为DG//AC,所以∠DEA = ∠EAC.
因为AF平分∠BAC,所以∠DAE = ∠EAC,
所以∠DAE = ∠DEA.