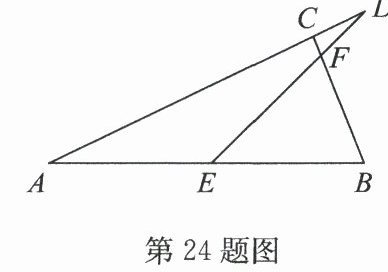
24.(8 分)如图,$ ∠ BCD = 94^{\circ} $,$ ∠ A = 26^{\circ} $,$ ∠ BED = 45^{\circ} $,求$ ∠ B $和$ ∠ BFD $的度数.

答案:24.解:因为∠BCD = 94°,∠A = 26°,
所以∠B = ∠BCD−∠A = 94°−26° = 68°,
因为∠BED = 45°,
所以∠BFD = ∠BED + ∠B = 45° + 68° = 113°
所以∠B = ∠BCD−∠A = 94°−26° = 68°,
因为∠BED = 45°,
所以∠BFD = ∠BED + ∠B = 45° + 68° = 113°
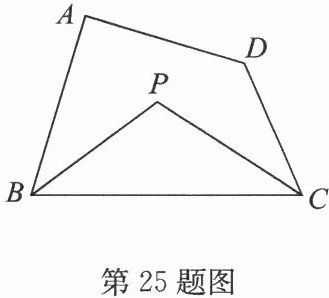
25.(8 分)(2025·钟吾初中期末)如图,在四边形 $ ABCD $中,$ BP $,$ CP $分别平分$ ∠ ABC $和$ ∠ BCD $. 若$ ∠ A = 90^{\circ} $,$ ∠ D = 130^{\circ} $,求$ ∠ P $的度数.

答案:25.解:因为∠A = 90°,∠D = 130°,
所以∠ABC + ∠BCD = 360°−∠A−∠D = 140°.
因为BP,CP分别平分∠ABC和∠BCD,
所以∠PBC = $\frac{1}{2}$∠ABC,∠PCB = $\frac{1}{2}$∠BCD,
所以∠PBC + ∠PCB = $\frac{1}{2}$∠ABC + $\frac{1}{2}$∠BCD = $\frac{1}{2}$(∠ABC + ∠BCD)= 70°,
所以∠P = 180°−(∠PBC + ∠PCB)= 180°−70° = 110°.
所以∠ABC + ∠BCD = 360°−∠A−∠D = 140°.
因为BP,CP分别平分∠ABC和∠BCD,
所以∠PBC = $\frac{1}{2}$∠ABC,∠PCB = $\frac{1}{2}$∠BCD,
所以∠PBC + ∠PCB = $\frac{1}{2}$∠ABC + $\frac{1}{2}$∠BCD = $\frac{1}{2}$(∠ABC + ∠BCD)= 70°,
所以∠P = 180°−(∠PBC + ∠PCB)= 180°−70° = 110°.
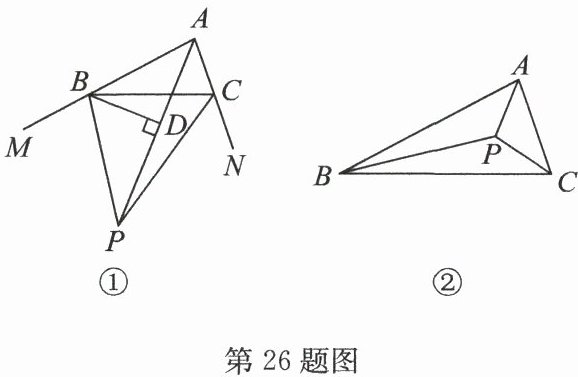
26.(8 分)(2025·宿城区期末)在$ △ ABC $中,记$ ∠ BAC = α $,$ ∠ ACB = β $.
(1)如图①,若 $ AP $平分$ ∠ BAC $,$ BP $,$ CP $分别平分$ △ ABC $的外角$ ∠ CBM $和$ ∠ BCN $,$ BD ⊥ AP $于点 $ D $.
①用含 $ α $的代数式表示$ ∠ BPC $的度数;
②用含 $ β $的代数式表示$ ∠ PBD $的度数.
(2)如图②,若 $ P $为$ △ ABC $的三条内角平分线的交点,且 $ BD ⊥ AP $于点 $ D $.
①请补全图形;
②猜想(1)中的两个结论是否发生变化? 如果不变,请说明理由;如果变化,直接写出正确的结论.
(1)如图①,若 $ AP $平分$ ∠ BAC $,$ BP $,$ CP $分别平分$ △ ABC $的外角$ ∠ CBM $和$ ∠ BCN $,$ BD ⊥ AP $于点 $ D $.
①用含 $ α $的代数式表示$ ∠ BPC $的度数;
②用含 $ β $的代数式表示$ ∠ PBD $的度数.
(2)如图②,若 $ P $为$ △ ABC $的三条内角平分线的交点,且 $ BD ⊥ AP $于点 $ D $.
①请补全图形;
②猜想(1)中的两个结论是否发生变化? 如果不变,请说明理由;如果变化,直接写出正确的结论.

答案:
26.解:(1)①
因为BP,CP分别平分△ABC的外角∠CBM 和∠BCN,
所以∠PBC = ∠PBM = $\frac{1}{2}$∠CBM = $\frac{1}{2}$(α + β),∠BCP = $\frac{1}{2}$∠BCN = $\frac{1}{2}$(180°−β),
所以∠BPC = 180°−∠PBC−∠BCP = 180°−$\frac{1}{2}$(α + β)−$\frac{1}{2}$(180°−β)= 90°−$\frac{1}{2}$α.
②在直角△PBD中,∠PBD = 90°−∠BPD,
因为∠BPD = ∠PBM−∠PAM = $\frac{1}{2}$(α + β)−$\frac{1}{2}$α = $\frac{1}{2}$β,
所以∠PBD = 90°−$\frac{1}{2}$β.
(2)①如答图所示.

②(1)中的两个结论发生了变化,∠BPC = 90°+$\frac{1}{2}$α,∠PBD = $\frac{1}{2}$β.
26.解:(1)①
因为BP,CP分别平分△ABC的外角∠CBM 和∠BCN,
所以∠PBC = ∠PBM = $\frac{1}{2}$∠CBM = $\frac{1}{2}$(α + β),∠BCP = $\frac{1}{2}$∠BCN = $\frac{1}{2}$(180°−β),
所以∠BPC = 180°−∠PBC−∠BCP = 180°−$\frac{1}{2}$(α + β)−$\frac{1}{2}$(180°−β)= 90°−$\frac{1}{2}$α.
②在直角△PBD中,∠PBD = 90°−∠BPD,
因为∠BPD = ∠PBM−∠PAM = $\frac{1}{2}$(α + β)−$\frac{1}{2}$α = $\frac{1}{2}$β,
所以∠PBD = 90°−$\frac{1}{2}$β.
(2)①如答图所示.

②(1)中的两个结论发生了变化,∠BPC = 90°+$\frac{1}{2}$α,∠PBD = $\frac{1}{2}$β.