1. 不等式组$\begin{cases}3x - 1 ≥ x + 1,\\x + 4 > 4x - 2\end{cases}$的解集是( )
A.$1 ≤ x < 2$
B.$x ≤ 1$
C.$x > 2$
D.$1 < x ≤ 2$
A.$1 ≤ x < 2$
B.$x ≤ 1$
C.$x > 2$
D.$1 < x ≤ 2$
答案:1. A
解析:
解不等式组:
1. 解不等式 $3x - 1 ≥ x + 1$:
$3x - x ≥ 1 + 1$
$2x ≥ 2$
$x ≥ 1$
2. 解不等式 $x + 4 > 4x - 2$:
$4 + 2 > 4x - x$
$6 > 3x$
$x < 2$
综上,不等式组的解集为 $1 ≤ x < 2$。
A
1. 解不等式 $3x - 1 ≥ x + 1$:
$3x - x ≥ 1 + 1$
$2x ≥ 2$
$x ≥ 1$
2. 解不等式 $x + 4 > 4x - 2$:
$4 + 2 > 4x - x$
$6 > 3x$
$x < 2$
综上,不等式组的解集为 $1 ≤ x < 2$。
A
2. (2025·怀文中学月考)若$a^x = 64$,$a^y = \frac{64}{a}$,用含$x$的代数式表示$y$是(
A.$y = x - 1$
B.$y = x + 1$
C.$x = y - 1$
D.$x = y + 1$
A
)A.$y = x - 1$
B.$y = x + 1$
C.$x = y - 1$
D.$x = y + 1$
答案:2. A
解析:
因为$a^y = \frac{64}{a} = 64 · a^{-1}$,又因为$a^x = 64$,所以$a^y = a^x · a^{-1} = a^{x - 1}$,则$y = x - 1$。
A
A
3. 若关于$x$,$y$的方程组$\begin{cases}3mx - y = n,\\2x + ny = m\end{cases}$的解为$\begin{cases}x = 1,\\y = 1\end{cases}$,则$(m - n)^2$等于( )
A.1
B.4
C.9
D.25
A.1
B.4
C.9
D.25
答案:3. B
解析:
将$\begin{cases}x = 1\\y = 1\end{cases}$代入方程组$\begin{cases}3mx - y = n\\2x + ny = m\end{cases}$,得:
$\begin{cases}3m×1 - 1 = n \\2×1 + n×1 = m\end{cases}$
化简为:
$\begin{cases}3m - n = 1 \\m - n = 2\end{cases}$
用第一个方程减第二个方程:$(3m - n) - (m - n) = 1 - 2$,即$2m = -1$,解得$m=-\dfrac{1}{2}$。
将$m=-\dfrac{1}{2}$代入$m - n = 2$,得$-\dfrac{1}{2} - n = 2$,解得$n=-\dfrac{5}{2}$。
则$m - n=-\dfrac{1}{2}-(-\dfrac{5}{2})=2$,$(m - n)^2=2^2 = 4$。
B
$\begin{cases}3m×1 - 1 = n \\2×1 + n×1 = m\end{cases}$
化简为:
$\begin{cases}3m - n = 1 \\m - n = 2\end{cases}$
用第一个方程减第二个方程:$(3m - n) - (m - n) = 1 - 2$,即$2m = -1$,解得$m=-\dfrac{1}{2}$。
将$m=-\dfrac{1}{2}$代入$m - n = 2$,得$-\dfrac{1}{2} - n = 2$,解得$n=-\dfrac{5}{2}$。
则$m - n=-\dfrac{1}{2}-(-\dfrac{5}{2})=2$,$(m - n)^2=2^2 = 4$。
B
4. 如图,在四边形$ABCD$中,$∠ ADC = ∠ ABC = 90°$,与$∠ ADC$,$∠ ABC$相邻的两外角的平分线交于点$E$,若$∠ A = 50°$,则$∠ E$的度数为(
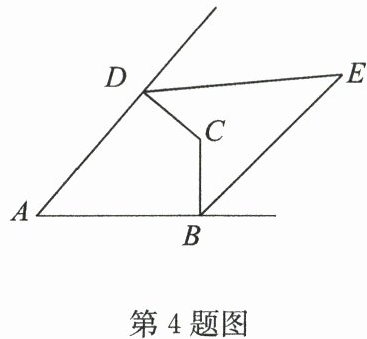
A.$60°$
B.$50°$
C.$40°$
D.$30°$
C
)
A.$60°$
B.$50°$
C.$40°$
D.$30°$
答案:4. C
解析:
解:在四边形$ABCD$中,$∠ ADC = ∠ ABC = 90°$,$∠ A = 50°$,
$∠ C=360°-∠ A-∠ ADC-∠ ABC=360° - 50° - 90° - 90°=130°$。
$∠ ADC$相邻外角为$180° - 90°=90°$,其平分线分外角为$45°$;
$∠ ABC$相邻外角为$180° - 90°=90°$,其平分线分外角为$45°$。
在四边形$BCDE$中,$∠ E=360° - ∠ C - 45° - 45°=360° - 130° - 90°=140°$,
$∠ E$为所求角的补角,故$∠ E=180° - 140°=40°$。
答案:C
$∠ C=360°-∠ A-∠ ADC-∠ ABC=360° - 50° - 90° - 90°=130°$。
$∠ ADC$相邻外角为$180° - 90°=90°$,其平分线分外角为$45°$;
$∠ ABC$相邻外角为$180° - 90°=90°$,其平分线分外角为$45°$。
在四边形$BCDE$中,$∠ E=360° - ∠ C - 45° - 45°=360° - 130° - 90°=140°$,
$∠ E$为所求角的补角,故$∠ E=180° - 140°=40°$。
答案:C
5. 定义一种新的运算:若$a ≠ 0$,则有$a※b = a^{-2} + ab + | - b |$,那么$(-\frac{1}{2})※2$的值是
5
.答案:5. 5
解析:
$(-\frac{1}{2})※2$
$=(-\frac{1}{2})^{-2}+(-\frac{1}{2})×2+|-2|$
$=4+(-1)+2$
$=5$
$=(-\frac{1}{2})^{-2}+(-\frac{1}{2})×2+|-2|$
$=4+(-1)+2$
$=5$
6. 已知关于$x$,$y$的二元一次方程组$\begin{cases}x + y = 1,\\x - y = a\end{cases}$的解满足$x > y$,则$a$的取值范围是 ______ .
答案:6. $ a > 0 $
解析:
解:解方程组$\begin{cases}x + y = 1 \\ x - y = a\end{cases}$,
两式相加得:$2x = 1 + a$,解得$x = \dfrac{1 + a}{2}$,
两式相减得:$2y = 1 - a$,解得$y = \dfrac{1 - a}{2}$,
因为$x > y$,所以$\dfrac{1 + a}{2} > \dfrac{1 - a}{2}$,
两边同时乘以$2$得:$1 + a > 1 - a$,
移项得:$a + a > 1 - 1$,
合并同类项得:$2a > 0$,
解得:$a > 0$。
$a > 0$
两式相加得:$2x = 1 + a$,解得$x = \dfrac{1 + a}{2}$,
两式相减得:$2y = 1 - a$,解得$y = \dfrac{1 - a}{2}$,
因为$x > y$,所以$\dfrac{1 + a}{2} > \dfrac{1 - a}{2}$,
两边同时乘以$2$得:$1 + a > 1 - a$,
移项得:$a + a > 1 - 1$,
合并同类项得:$2a > 0$,
解得:$a > 0$。
$a > 0$
7. 如图,$∠ ABC = 40°$,$D$为$∠ ABC$内部的一点,以$D$为顶点,作$∠ EDF$,使得$DE // BC$,$DF // AB$,则$∠ EDF =$
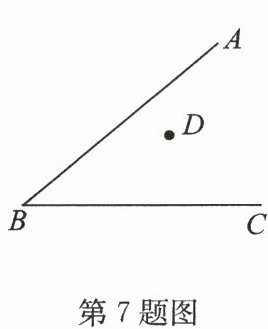
$ 40 ^ { \circ } $或$ 140 ^ { \circ } $
.
答案:7. $ 40 ^ { \circ } $或$ 140 ^ { \circ } $
解析:
解:分两种情况:
当$DE$与$BA$同向,$DF$与$BC$同向时,
因为$DE// BC$,所以$∠ EDB+∠ ABC=180°$,
因为$DF// AB$,所以$∠ FDB+∠ ABC=180°$,
所以$∠ EDF=∠ ABC=40°$;
当$DE$与$BA$反向,$DF$与$BC$同向时,
因为$DE// BC$,所以$∠ EDB=∠ ABC=40°$,
因为$DF// AB$,所以$∠ FDB=180°-∠ ABC=140°$,
所以$∠ EDF=180°-40°=140°$。
综上,$∠ EDF=40°$或$140°$。
当$DE$与$BA$同向,$DF$与$BC$同向时,
因为$DE// BC$,所以$∠ EDB+∠ ABC=180°$,
因为$DF// AB$,所以$∠ FDB+∠ ABC=180°$,
所以$∠ EDF=∠ ABC=40°$;
当$DE$与$BA$反向,$DF$与$BC$同向时,
因为$DE// BC$,所以$∠ EDB=∠ ABC=40°$,
因为$DF// AB$,所以$∠ FDB=180°-∠ ABC=140°$,
所以$∠ EDF=180°-40°=140°$。
综上,$∠ EDF=40°$或$140°$。
8. 对于有理数$x$,我们规定$\{x\}$表示不小于$x$的最小整数,如$\{2.2\} = 3$,$\{2\} = 2$,$\{ - 2.5\} = - 2$,若$\{\frac{x + 4}{10}\} = 3$,则$x$的取值范围是
$ 16 < x ≤ 26 $
.答案:8. $ 16 < x ≤ 26 $
解析:
解:由题意得,$2 < \frac{x + 4}{10} ≤ 3$
两边同时乘以10:$20 < x + 4 ≤ 30$
两边同时减去4:$16 < x ≤ 26$
$16 < x ≤ 26$
两边同时乘以10:$20 < x + 4 ≤ 30$
两边同时减去4:$16 < x ≤ 26$
$16 < x ≤ 26$