9. (10分)如图,在正方形网格中,每个小正方形的边长均为1个单位长度,$△ ABC$的三个顶点都在网格顶点处,按要求画图:
(1)将$△ ABC$平移到$△ A_1B_1C_1$的位置,点$C$的对应点为$C_1$,画出$△ A_1B_1C_1$;
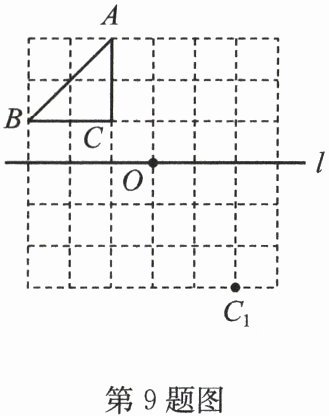
(2)将$△ ABC$绕点$O$顺时针旋转$90°$得到$△ A_2B_2C_2$,画出$△ A_2B_2C_2$;
(3)$△ A_3B_3C_3$与$△ ABC$关于直线$l$对称,画出$△ A_3B_3C_3$.
(1)将$△ ABC$平移到$△ A_1B_1C_1$的位置,点$C$的对应点为$C_1$,画出$△ A_1B_1C_1$;

(2)将$△ ABC$绕点$O$顺时针旋转$90°$得到$△ A_2B_2C_2$,画出$△ A_2B_2C_2$;
(3)$△ A_3B_3C_3$与$△ ABC$关于直线$l$对称,画出$△ A_3B_3C_3$.
答案:
9. 解: (1)(2)(3)如答图所示.
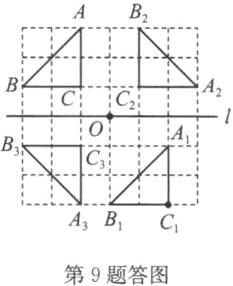
9. 解: (1)(2)(3)如答图所示.

10. (10分)(2024·常州)解方程组和不等式组:
(1)$\begin{cases}x - y = 0,\\3x + y = 4;\end{cases}$
(2)$\begin{cases}3x - 6 < 0,\frac{x - 1}{2} < x.\end{cases}$
(1)$\begin{cases}x - y = 0,\\3x + y = 4;\end{cases}$
(2)$\begin{cases}3x - 6 < 0,\frac{x - 1}{2} < x.\end{cases}$
答案:10. 解: (1)$ \{ \begin{array} { l } { x - y = 0 , ① } \\ { 3 x + y = 4 , ② } \end{array} $
①+②, 得$ 4 x = 4 $, 解得$ x = 1 $.
把$ x = 1 $代入①, 得$ y = 1 $.
所以原方程组的解为$ \{ \begin{array} { l } { x = 1 , } \\ { y = 1 . } \end{array} $
(2)$ \{ \begin{array} { l } { 3 x - 6 < 0 , ① } \\ { \frac { x - 1 } { 2 } < x , ② } \end{array} $
解不等式①, 得$ x < 2 $.
解不等式②, 得$ x > - 1 $.
所以原不等式组的解集为$ - 1 < x < 2 $.
①+②, 得$ 4 x = 4 $, 解得$ x = 1 $.
把$ x = 1 $代入①, 得$ y = 1 $.
所以原方程组的解为$ \{ \begin{array} { l } { x = 1 , } \\ { y = 1 . } \end{array} $
(2)$ \{ \begin{array} { l } { 3 x - 6 < 0 , ① } \\ { \frac { x - 1 } { 2 } < x , ② } \end{array} $
解不等式①, 得$ x < 2 $.
解不等式②, 得$ x > - 1 $.
所以原不等式组的解集为$ - 1 < x < 2 $.
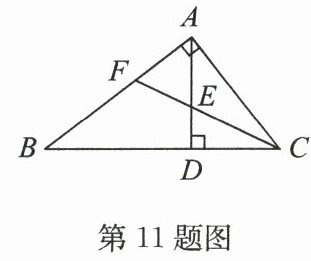
11. (16分)如图,在$△ ABC$中,$∠ BAC = 90°$,$AD$是$BC$边上的高,$CF$平分$∠ ACB$,分别交$AD$,$AB$于点$E$,$F$.
求证:(1)$∠ DAC = ∠ ABC$;
(2)$∠ AFE = ∠ AEF$.
求证:(1)$∠ DAC = ∠ ABC$;
(2)$∠ AFE = ∠ AEF$.

答案:11. 证明: (1)因为$ ∠ B A C = 90 ^ { \circ } $,
所以$ ∠ A B C + ∠ A C B = 90 ^ { \circ } $.
因为AD是BC边上的高, 所以$ A D ⊥ B C $,
所以$ ∠ A D C = 90 ^ { \circ } $, 所以$ ∠ D A C + ∠ A C B = 90 ^ { \circ } $,
所以$ ∠ D A C = ∠ A B C $.
(2)因为CF平分$ ∠ A C B $, 所以$ ∠ A C F = ∠ B C F $.
因为$ ∠ B A C = ∠ A D C = 90 ^ { \circ } $,
所以$ ∠ A F E + ∠ A C F = ∠ C E D + ∠ B C F = 90 ^ { \circ } $,
所以$ ∠ A F E = ∠ C E D $.
又因为$ ∠ A E F = ∠ C E D $, 所以$ ∠ A F E = ∠ A E F $.
所以$ ∠ A B C + ∠ A C B = 90 ^ { \circ } $.
因为AD是BC边上的高, 所以$ A D ⊥ B C $,
所以$ ∠ A D C = 90 ^ { \circ } $, 所以$ ∠ D A C + ∠ A C B = 90 ^ { \circ } $,
所以$ ∠ D A C = ∠ A B C $.
(2)因为CF平分$ ∠ A C B $, 所以$ ∠ A C F = ∠ B C F $.
因为$ ∠ B A C = ∠ A D C = 90 ^ { \circ } $,
所以$ ∠ A F E + ∠ A C F = ∠ C E D + ∠ B C F = 90 ^ { \circ } $,
所以$ ∠ A F E = ∠ C E D $.
又因为$ ∠ A E F = ∠ C E D $, 所以$ ∠ A F E = ∠ A E F $.
12. (16分)某中学为促进阳光体育运动发展,计划购进足球、排球充实体育器材,若购买足球30个,排球20个,共需资金2600元;若购买足球40个,排球30个,共需资金3600元.
(1)分别求足球、排球的单价;
(2)若该校计划购进这两种球共60个,学校最多能够提供资金2800元,则最多能购买足球多少个?
(1)分别求足球、排球的单价;
(2)若该校计划购进这两种球共60个,学校最多能够提供资金2800元,则最多能购买足球多少个?
答案:12. 解: (1)设足球、排球的单价分别为x元,y元, 根据题意, 得$ \{ \begin{array} { l } { 30 x + 20 y = 2600 , } \\ { 40 x + 30 y = 3600 , } \end{array} $解得$ \{ \begin{array} { l } { x = 60 , } \\ { y = 40 . } \end{array} $
答: 足球的单价为60元, 排球的单价为40元.
(2)设购买足球x个, 则购买排球$ ( 60 - x ) $个, 根据题意, 得$ 60 x + 40 ( 60 - x ) ≤ 2800 $,
解得$ x ≤ 20 $.
答: 最多能购买足球20个.
答: 足球的单价为60元, 排球的单价为40元.
(2)设购买足球x个, 则购买排球$ ( 60 - x ) $个, 根据题意, 得$ 60 x + 40 ( 60 - x ) ≤ 2800 $,
解得$ x ≤ 20 $.
答: 最多能购买足球20个.