1. 关于$(a - b)(a^{2} + b) - a(a^{2} - ab + b)$的计算结果,下列说法中正确的是(
A.与字母$a$的取值无关
B.与字母$b$的取值无关
C.与字母$a,b$的取值都无关
D.以上都不正确
A
)A.与字母$a$的取值无关
B.与字母$b$的取值无关
C.与字母$a,b$的取值都无关
D.以上都不正确
答案:1. A
解析:
$\begin{aligned}&(a - b)(a^{2} + b) - a(a^{2} - ab + b)\\=&a^{3} + ab - a^{2}b - b^{2} - (a^{3} - a^{2}b + ab)\\=&a^{3} + ab - a^{2}b - b^{2} - a^{3} + a^{2}b - ab\\=&-b^{2}\end{aligned}$
结果为$-b^{2}$,与字母$a$的取值无关。
A
结果为$-b^{2}$,与字母$a$的取值无关。
A
2. (2025·昆山期末)已知关于$x$的不等式组$\begin{cases}x - 2 < 3x - 6, \\x < m\end{cases}$无解,那么$m$的取值范围是( )
A.$m < 2$
B.$m > 2$
C.$m≤ 2$
D.$m≥ 2$
A.$m < 2$
B.$m > 2$
C.$m≤ 2$
D.$m≥ 2$
答案:2. C
解析:
解不等式组:
1. 解$x - 2 < 3x - 6$,移项得$x - 3x < -6 + 2$,即$-2x < -4$,两边同时除以$-2$,不等号方向改变,得$x > 2$。
2. 第二个不等式为$x < m$。
因为不等式组无解,所以$x > 2$与$x < m$没有公共部分,即$m ≤ 2$。
C
1. 解$x - 2 < 3x - 6$,移项得$x - 3x < -6 + 2$,即$-2x < -4$,两边同时除以$-2$,不等号方向改变,得$x > 2$。
2. 第二个不等式为$x < m$。
因为不等式组无解,所以$x > 2$与$x < m$没有公共部分,即$m ≤ 2$。
C
3. (2024·溧阳期末)下列命题的逆命题是真命题的是(
A.同位角相等
B.若$x > 0,y > 0$,则$x + y > 0$
C.若$x + y = 0$,则$x$与$y$互为相反数
D.若$a = b$,则$a^{2} = b^{2}$
C
)A.同位角相等
B.若$x > 0,y > 0$,则$x + y > 0$
C.若$x + y = 0$,则$x$与$y$互为相反数
D.若$a = b$,则$a^{2} = b^{2}$
答案:3. C
4. 某校开展消防安全知识竞赛,计划拿出 1800 元钱全部用于购买甲、乙两种奖品(两种奖品都购买)奖励表现突出的班级,已知甲种奖品每件 150 元,乙种奖品每件 100 元,则购买方案有(
A.5 种
B.6 种
C.7 种
D.8 种
A
)A.5 种
B.6 种
C.7 种
D.8 种
答案:4. A
解析:
设购买甲种奖品$x$件,乙种奖品$y$件。
由题意得:$150x + 100y = 1800$,化简得$3x + 2y = 36$,即$y = \frac{36 - 3x}{2}$。
因为$x$,$y$为正整数,所以$36 - 3x$必须为正偶数,$3x$为偶数,$x$为偶数。
$x > 0$,$y > 0$,则$\frac{36 - 3x}{2} > 0$,解得$x < 12$。
$x$可取2,4,6,8,10,共5种。
A
由题意得:$150x + 100y = 1800$,化简得$3x + 2y = 36$,即$y = \frac{36 - 3x}{2}$。
因为$x$,$y$为正整数,所以$36 - 3x$必须为正偶数,$3x$为偶数,$x$为偶数。
$x > 0$,$y > 0$,则$\frac{36 - 3x}{2} > 0$,解得$x < 12$。
$x$可取2,4,6,8,10,共5种。
A
5. 已知$1 = 1^{2},1 + 3 = 2^{2},1 + 3 + 5 = 3^{2},···$,则$1 + 3 + 5 + 7 + ··· + 2025 = $(
A.$1012^{2}$
B.$1013^{2}$
C.$2024^{2}$
D.$2025^{2}$
B
)A.$1012^{2}$
B.$1013^{2}$
C.$2024^{2}$
D.$2025^{2}$
答案:5. B
解析:
观察已知等式:$1 = 1^{2}$,$1 + 3 = 2^{2}$,$1 + 3 + 5 = 3^{2}$,···,规律为从1开始的连续n个奇数的和等于$n^{2}$。
数列$1, 3, 5, ···, 2025$是首项为1,公差为2的等差数列,设项数为n,由通项公式$a_n = 1 + (n - 1)×2 = 2n - 1$,令$2n - 1 = 2025$,解得$n = 1013$。
所以$1 + 3 + 5 + ··· + 2025 = 1013^{2}$
B
数列$1, 3, 5, ···, 2025$是首项为1,公差为2的等差数列,设项数为n,由通项公式$a_n = 1 + (n - 1)×2 = 2n - 1$,令$2n - 1 = 2025$,解得$n = 1013$。
所以$1 + 3 + 5 + ··· + 2025 = 1013^{2}$
B
6. 若$2x^{2} - x - 7 = 0$,则$x(x - 3) + (x + 1)^{2} = $
8
.答案:6. 8
解析:
$x(x - 3) + (x + 1)^{2}$
$=x^{2}-3x+x^{2}+2x + 1$
$=2x^{2}-x + 1$
因为$2x^{2}-x - 7 = 0$,所以$2x^{2}-x=7$。
则$2x^{2}-x + 1=7 + 1=8$
8
$=x^{2}-3x+x^{2}+2x + 1$
$=2x^{2}-x + 1$
因为$2x^{2}-x - 7 = 0$,所以$2x^{2}-x=7$。
则$2x^{2}-x + 1=7 + 1=8$
8
7. 当$x = $
-1 或 -2
时,$(2x + 3)^{x + 2} = 1$.答案:7. -1 或 -2
解析:
分三种情况讨论:
1. 当指数为0,底数不为0时:$x + 2 = 0$,解得$x = -2$,此时底数$2x + 3 = 2×(-2) + 3 = -1 ≠ 0$,符合题意;
2. 当底数为1时:$2x + 3 = 1$,解得$x = -1$,此时指数$x + 2 = -1 + 2 = 1$,$1^1 = 1$,符合题意;
3. 当底数为-1,指数为偶数时:$2x + 3 = -1$,解得$x = -2$,此时指数$x + 2 = 0$,$0$是偶数,$(-1)^0 = 1$,但此情况与第一种情况结果相同。
综上,$x = -1$或$x = -2$。
-1 或 -2
1. 当指数为0,底数不为0时:$x + 2 = 0$,解得$x = -2$,此时底数$2x + 3 = 2×(-2) + 3 = -1 ≠ 0$,符合题意;
2. 当底数为1时:$2x + 3 = 1$,解得$x = -1$,此时指数$x + 2 = -1 + 2 = 1$,$1^1 = 1$,符合题意;
3. 当底数为-1,指数为偶数时:$2x + 3 = -1$,解得$x = -2$,此时指数$x + 2 = 0$,$0$是偶数,$(-1)^0 = 1$,但此情况与第一种情况结果相同。
综上,$x = -1$或$x = -2$。
-1 或 -2
8. 如图,一副三角尺按如图所示放置($∠ C = 60^{\circ},∠ D = 45^{\circ}$),则$∠ DFB = $
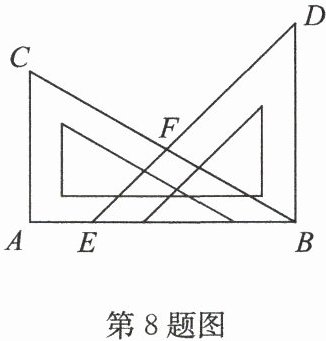
75°
.
答案:8. 75°
解析:
解:由题意知,三角尺中,$∠C=60^{\circ}$,$∠D=45^{\circ}$,则$∠ABC=30^{\circ}$,$∠BAD=90^{\circ}$,$∠ABD=45^{\circ}$。
在$△ ABE$中,$∠AEB=180^{\circ}-∠A-∠ABE=180^{\circ}-90^{\circ}-30^{\circ}=60^{\circ}$,所以$∠FED=∠AEB=60^{\circ}$。
在$△ FED$中,$∠DFB=∠D+∠FED=45^{\circ}+30^{\circ}=75^{\circ}$。
$75^{\circ}$
在$△ ABE$中,$∠AEB=180^{\circ}-∠A-∠ABE=180^{\circ}-90^{\circ}-30^{\circ}=60^{\circ}$,所以$∠FED=∠AEB=60^{\circ}$。
在$△ FED$中,$∠DFB=∠D+∠FED=45^{\circ}+30^{\circ}=75^{\circ}$。
$75^{\circ}$
9. (2024·大庆)不等式组$\begin{cases}x > \dfrac{x - 2}{2}, \\5x - 3 < 9 + x\end{cases}$的整数解有 ______ 个.
答案:9. 4
解析:
解不等式组:
1. 解不等式 $x > \dfrac{x - 2}{2}$:
两边同乘2得:$2x > x - 2$,
移项得:$2x - x > -2$,
解得:$x > -2$。
2. 解不等式 $5x - 3 < 9 + x$:
移项得:$5x - x < 9 + 3$,
合并同类项得:$4x < 12$,
解得:$x < 3$。
不等式组的解集为$-2 < x < 3$,整数解为$-1, 0, 1, 2$,共4个。
4
1. 解不等式 $x > \dfrac{x - 2}{2}$:
两边同乘2得:$2x > x - 2$,
移项得:$2x - x > -2$,
解得:$x > -2$。
2. 解不等式 $5x - 3 < 9 + x$:
移项得:$5x - x < 9 + 3$,
合并同类项得:$4x < 12$,
解得:$x < 3$。
不等式组的解集为$-2 < x < 3$,整数解为$-1, 0, 1, 2$,共4个。
4