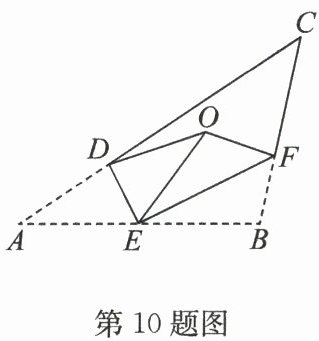
10. (2025·宿豫区期末)如图,将$△ ABC$沿$DE,EF$翻折,顶点$A,B$均落在点$O$处,且$EA$与$EB$重合于线段$EO$.若$∠ CDO + ∠ CFO = 88^{\circ}$,则$∠ C$的度数为
46
$^{\circ}$.
答案:10. 46
解析:
证明:由翻折性质得,∠A=∠DOE,∠B=∠FOE,∠ADO=2∠CDO,∠BFO=2∠CFO。
∵EA与EB重合于EO,
∴∠AOB=∠DOE+∠FOE=∠A+∠B。
∵∠CDO+∠CFO=88°,
∴∠ADO+∠BFO=2×88°=176°。
∵四边形ADOE、四边形BFOE内角和均为360°,
∴∠A+∠DOE+∠ADO+∠AEO=360°,∠B+∠FOE+∠BFO+∠BEO=360°。
又∠AEO+∠BEO=180°,∠A=∠DOE,∠B=∠FOE,
∴2∠A+∠ADO+2∠B+∠BFO+180°=720°,
即2(∠A+∠B)+176°=540°,解得∠A+∠B=182°。
在△ABC中,∠C=180°-(∠A+∠B)=180°-134°=46°。
46
∵EA与EB重合于EO,
∴∠AOB=∠DOE+∠FOE=∠A+∠B。
∵∠CDO+∠CFO=88°,
∴∠ADO+∠BFO=2×88°=176°。
∵四边形ADOE、四边形BFOE内角和均为360°,
∴∠A+∠DOE+∠ADO+∠AEO=360°,∠B+∠FOE+∠BFO+∠BEO=360°。
又∠AEO+∠BEO=180°,∠A=∠DOE,∠B=∠FOE,
∴2∠A+∠ADO+2∠B+∠BFO+180°=720°,
即2(∠A+∠B)+176°=540°,解得∠A+∠B=182°。
在△ABC中,∠C=180°-(∠A+∠B)=180°-134°=46°。
46
11. (16 分)(1)解方程组:$\begin{cases}3x - y = 5, \\5x + 2y = 23;\end{cases}$
(2)解不等式组:$\begin{cases}2x - 5 < 3x + 4, \\\dfrac{1 - x}{3} > \dfrac{x}{2}.\end{cases}$
(2)解不等式组:$\begin{cases}2x - 5 < 3x + 4, \\\dfrac{1 - x}{3} > \dfrac{x}{2}.\end{cases}$
答案:11. 解: (1) $\begin{cases}3x - y = 5,①\\5x + 2y = 23,②\end{cases}$
由①, 得 $y = 3x - 5$.
把 $y = 3x - 5$ 代入②, 得 $5x + 2(3x - 5) = 23$,
解得 $x = 3$.
把 $x = 3$ 代入①, 得 $y = 4$.
所以原方程组的解为 $\begin{cases}x = 3,\\y = 4.\end{cases}$
(2) $\begin{cases}2x - 5 < 3x + 4,①\\\dfrac{1 - x}{3} > \dfrac{x}{2},②\end{cases}$
解不等式①, 得 $x > -9$, 解不等式②, 得 $x < \dfrac{2}{5}$,
所以原不等式组的解集为 $-9 < x < \dfrac{2}{5}$.
由①, 得 $y = 3x - 5$.
把 $y = 3x - 5$ 代入②, 得 $5x + 2(3x - 5) = 23$,
解得 $x = 3$.
把 $x = 3$ 代入①, 得 $y = 4$.
所以原方程组的解为 $\begin{cases}x = 3,\\y = 4.\end{cases}$
(2) $\begin{cases}2x - 5 < 3x + 4,①\\\dfrac{1 - x}{3} > \dfrac{x}{2},②\end{cases}$
解不等式①, 得 $x > -9$, 解不等式②, 得 $x < \dfrac{2}{5}$,
所以原不等式组的解集为 $-9 < x < \dfrac{2}{5}$.
12. (16 分)(2024·贵州)为增强学生的劳动意识,养成劳动的习惯和品质,某校组织学生参加劳动实践.经学校与劳动基地联系,计划组织学生种植甲、乙两种作物.如果种植 3 亩甲作物和 2 亩乙作物需要 27 名学生,种植 2 亩甲作物和 2 亩乙作物需要 22 名学生.
根据以上信息,解答下列问题:
(1)种植 1 亩甲作物和 1 亩乙作物分别需要多少名学生?
(2)种植甲、乙两种作物共 10 亩,所需学生人数不超过 55 人,至少种植甲作物多少亩?
根据以上信息,解答下列问题:
(1)种植 1 亩甲作物和 1 亩乙作物分别需要多少名学生?
(2)种植甲、乙两种作物共 10 亩,所需学生人数不超过 55 人,至少种植甲作物多少亩?
答案:12. 解: (1) 设种植 1 亩甲作物需要 $x$ 名学生, 种植 1 亩乙作物需要 $y$ 名学生.
根据题意, 得 $\begin{cases}3x + 2y = 27,\\2x + 2y = 22,\end{cases}$ 解得 $\begin{cases}x = 5,\\y = 6.\end{cases}$
答: 种植 1 亩甲作物需要 5 名学生, 种植 1 亩乙作物需要 6 名学生.
(2) 设种植甲作物 $m$ 亩, 则种植乙作物 $(10 - m)$ 亩.
根据题意, 得 $5m + 6(10 - m) ≤ 55$, 解得 $m ≥ 5$.
答: 至少种植甲作物 5 亩.
根据题意, 得 $\begin{cases}3x + 2y = 27,\\2x + 2y = 22,\end{cases}$ 解得 $\begin{cases}x = 5,\\y = 6.\end{cases}$
答: 种植 1 亩甲作物需要 5 名学生, 种植 1 亩乙作物需要 6 名学生.
(2) 设种植甲作物 $m$ 亩, 则种植乙作物 $(10 - m)$ 亩.
根据题意, 得 $5m + 6(10 - m) ≤ 55$, 解得 $m ≥ 5$.
答: 至少种植甲作物 5 亩.
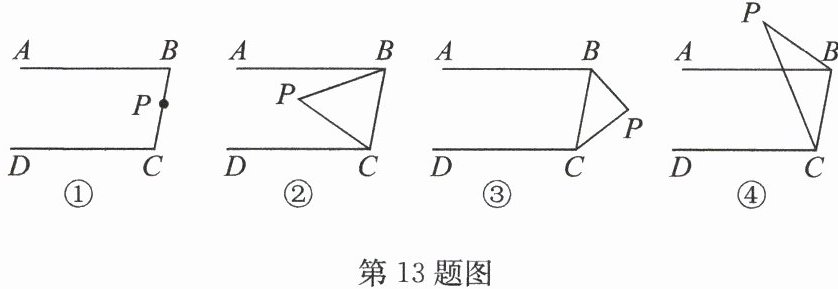
13. (18 分)观察发现:
已知$AB// CD,P$是平面上一个动点.当点$P$在直线$AB,CD$之间,且在$BC$(不与点$B,C$重合)上时,如图①,容易发现:$∠ ABP + ∠ DCP = ∠ BPC$.
拓展探究:
(1)当点$P$位于直线$AB,CD$之间,且在$BC$左侧时,如图②,$∠ ABP,∠ DCP,∠ BPC$之间有何关系? 请说明理由;
(2)当点$P$位于直线$AB,CD$之间,且在$BC$右侧时,如图③,直接写出$∠ ABP,∠ DCP,∠ BPC$之间的关系;
(3)当点$P$位于直线$AB,CD$的同侧时,如图④,直接写出$∠ ABP,∠ DCP,∠ BPC$之间的关系.
已知$AB// CD,P$是平面上一个动点.当点$P$在直线$AB,CD$之间,且在$BC$(不与点$B,C$重合)上时,如图①,容易发现:$∠ ABP + ∠ DCP = ∠ BPC$.
拓展探究:
(1)当点$P$位于直线$AB,CD$之间,且在$BC$左侧时,如图②,$∠ ABP,∠ DCP,∠ BPC$之间有何关系? 请说明理由;
(2)当点$P$位于直线$AB,CD$之间,且在$BC$右侧时,如图③,直接写出$∠ ABP,∠ DCP,∠ BPC$之间的关系;
(3)当点$P$位于直线$AB,CD$的同侧时,如图④,直接写出$∠ ABP,∠ DCP,∠ BPC$之间的关系.

答案:
13. 解: (1) $∠ ABP + ∠ DCP = ∠ BPC$.
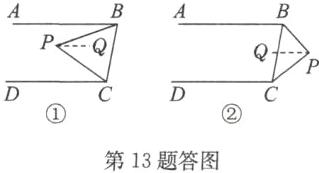
理由: 如答图①, 过点 $P$ 作直线 $PQ // AB$,
所以 $∠ ABP = ∠ BPQ$.
因为 $AB // CD$, 所以 $DC // PQ$,
所以 $∠ DCP = ∠ CPQ$,
所以 $∠ ABP + ∠ DCP = ∠ BPQ + ∠ CPQ = ∠ BPC$.
(2) $∠ ABP + ∠ BPC + ∠ DCP = 360^{\circ}$.
理由: 如答图②, 过点 $P$ 作 $PQ // AB$, 则 $DC // PQ$,
所以 $∠ ABP + ∠ BPQ = 180^{\circ}$, $∠ DCP + ∠ CPQ = 180^{\circ}$,
所以 $∠ ABP + ∠ BPQ + ∠ CPQ + ∠ DCP = 360^{\circ}$,
即 $∠ ABP + ∠ BPC + ∠ DCP = 360^{\circ}$.
(3) $∠ BPC = ∠ DCP - ∠ ABP$.
13. 解: (1) $∠ ABP + ∠ DCP = ∠ BPC$.
理由: 如答图①, 过点 $P$ 作直线 $PQ // AB$,
所以 $∠ ABP = ∠ BPQ$.
因为 $AB // CD$, 所以 $DC // PQ$,
所以 $∠ DCP = ∠ CPQ$,
所以 $∠ ABP + ∠ DCP = ∠ BPQ + ∠ CPQ = ∠ BPC$.

(2) $∠ ABP + ∠ BPC + ∠ DCP = 360^{\circ}$.
理由: 如答图②, 过点 $P$ 作 $PQ // AB$, 则 $DC // PQ$,
所以 $∠ ABP + ∠ BPQ = 180^{\circ}$, $∠ DCP + ∠ CPQ = 180^{\circ}$,
所以 $∠ ABP + ∠ BPQ + ∠ CPQ + ∠ DCP = 360^{\circ}$,
即 $∠ ABP + ∠ BPC + ∠ DCP = 360^{\circ}$.
(3) $∠ BPC = ∠ DCP - ∠ ABP$.