1. 下列运算正确的是 (
A.$x^{6}÷ x^{2}=x^{3}$
B.$a(x - y)=ax - ay$
C.$(-x^{2}y)^{3}=x^{6}y^{3}$
D.$(x - y)^{2}=x^{2}-y^{2}$
B
)A.$x^{6}÷ x^{2}=x^{3}$
B.$a(x - y)=ax - ay$
C.$(-x^{2}y)^{3}=x^{6}y^{3}$
D.$(x - y)^{2}=x^{2}-y^{2}$
答案:1. B
2. 已知不等式组$\begin{cases}x + 1< 2a,\\x - b> 1\end{cases}$的解集是$2< x< 3$,则关于$x$的方程$ax + b = 0$的解是 ( )
A.$x = 0$
B.$x=\frac{1}{2}$
C.$x = 1$
D.$x=-\frac{1}{2}$
A.$x = 0$
B.$x=\frac{1}{2}$
C.$x = 1$
D.$x=-\frac{1}{2}$
答案:2. D
解析:
解:解不等式组$\begin{cases}x + 1< 2a \\x - b> 1\end{cases}$,得$b + 1<x<2a - 1$。
因为解集是$2<x<3$,所以$\begin{cases}b + 1 = 2 \\2a - 1 = 3\end{cases}$,解得$\begin{cases}a = 2 \\b = 1\end{cases}$。
方程$ax + b = 0$为$2x + 1 = 0$,解得$x=-\frac{1}{2}$。
D
因为解集是$2<x<3$,所以$\begin{cases}b + 1 = 2 \\2a - 1 = 3\end{cases}$,解得$\begin{cases}a = 2 \\b = 1\end{cases}$。
方程$ax + b = 0$为$2x + 1 = 0$,解得$x=-\frac{1}{2}$。
D
3. (2024·天津)《孙子算经》是我国古代著名的数学典籍,其中有一道题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳度之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 4.5 尺;将绳子对折再量长木,长木还剩余 1 尺. 问木长多少尺? 设木长$x$尺,绳子长$y$尺,则可以列出的方程组为 (
A.$\begin{cases}y - x = 4.5,\\x - 0.5y = 1\end{cases}$
B.$\begin{cases}y - x = 4.5,\\x + 0.5y = 1\end{cases}$
C.$\begin{cases}x + y = 4.5,\\x - y = 1\end{cases}$
D.$\begin{cases}x + y = 4.5,\\y - x = 1\end{cases}$
A
)A.$\begin{cases}y - x = 4.5,\\x - 0.5y = 1\end{cases}$
B.$\begin{cases}y - x = 4.5,\\x + 0.5y = 1\end{cases}$
C.$\begin{cases}x + y = 4.5,\\x - y = 1\end{cases}$
D.$\begin{cases}x + y = 4.5,\\y - x = 1\end{cases}$
答案:3. A
4. (2024·江宁区期末)如图,在$△ ABC$中,$∠ CAB = 75^{\circ}$,将$△ ABC$绕点$A$旋转到$△ AB'C'$的位置,使得$CC'// AB$,则$∠ BAB'$的度数是 (
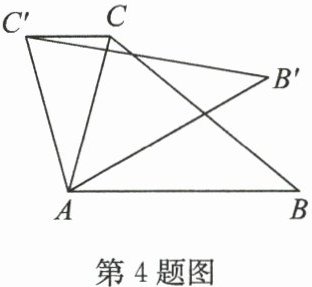
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
A
)
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
答案:4. A
解析:
解:
∵△ABC绕点A旋转到△AB'C'的位置,
∴AC=AC',∠BAB'=∠CAC',
∴△ACC'是等腰三角形,
∴∠ACC'=∠AC'C,
∵CC'//AB,∠CAB=75°,
∴∠ACC'=∠CAB=75°,
∴∠CAC'=180°-2∠ACC'=180°-2×75°=30°,
∴∠BAB'=30°。
A
∵△ABC绕点A旋转到△AB'C'的位置,
∴AC=AC',∠BAB'=∠CAC',
∴△ACC'是等腰三角形,
∴∠ACC'=∠AC'C,
∵CC'//AB,∠CAB=75°,
∴∠ACC'=∠CAB=75°,
∴∠CAC'=180°-2∠ACC'=180°-2×75°=30°,
∴∠BAB'=30°。
A
5. 若二元一次方程$2x + ay = 7$有一个解是$\begin{cases}x = 3,\\y = -1,\end{cases}$则$a$的值为 ______ .
答案:5. -1
解析:
将$\begin{cases}x = 3,\\y = -1\end{cases}$代入方程$2x + ay = 7$,得$2×3 + a×(-1) = 7$,即$6 - a = 7$,解得$a = -1$。
-1
-1
6. (2024·宿城区期末)同角的余角相等的逆命题是
如果两个角相等,那么这两个角是同一个角的余角
,它是一个假
命题(填“真”或“假”).答案:6. 如果两个角相等,那么这两个角是同一个角的余角 假
7. (2024·姜堰区期末)若用反证法证明命题“四边形中至少有一个角是直角或钝角”时,则首先应该提出的假设是:这个四边形中
所有的内角都是锐角
.答案:7. 所有的内角都是锐角
8. 若$x^{2}-5x + 3 = 0$,则$x(x - 1)(x - 2)(x - 3)(x - 4)(x - 5)=$.
答案:8. -9
解析:
由$x^{2}-5x + 3 = 0$,得$x^{2}=5x - 3$,$x^{2}-5x=-3$。
$x(x - 1)(x - 2)(x - 3)(x - 4)(x - 5)$
$=[x(x - 5)][(x - 1)(x - 4)][(x - 2)(x - 3)]$
$=(x^{2}-5x)(x^{2}-5x + 4)(x^{2}-5x + 6)$
将$x^{2}-5x=-3$代入上式:
$=(-3)[(-3) + 4][(-3) + 6]$
$=(-3)(1)(3)$
$=-9$
-9
$x(x - 1)(x - 2)(x - 3)(x - 4)(x - 5)$
$=[x(x - 5)][(x - 1)(x - 4)][(x - 2)(x - 3)]$
$=(x^{2}-5x)(x^{2}-5x + 4)(x^{2}-5x + 6)$
将$x^{2}-5x=-3$代入上式:
$=(-3)[(-3) + 4][(-3) + 6]$
$=(-3)(1)(3)$
$=-9$
-9
9. (10 分)(2025·宿城区期末)先化简,再求值:$(a - 2)^{2}+(a + 1)(a - 1)-2a(a - 3)$,其中$a=-\frac{1}{4}$.
答案:9. 解:原式$=a^{2}-4a+4+a^{2}-1-2a^{2}+6a=2a+3$,
当$a=-\frac {1}{4}$时,原式$=2×(-\frac {1}{4})+3=\frac {5}{2}$。
当$a=-\frac {1}{4}$时,原式$=2×(-\frac {1}{4})+3=\frac {5}{2}$。