新知梳理
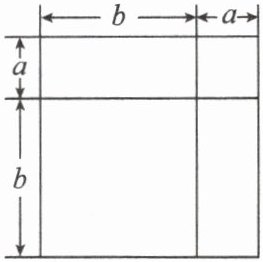
1. (1)如图,该图形可以看成是一个边长为$(a + b)$的大正方形,面积为
(2)一般地,对于任意的$a$,$b$,由多项式乘多项式法则可以得到:$(a + b)^2 = (a + b)(a + b) =$
2. 完全平方公式:$(a + b)^2 =$
1. (1)如图,该图形可以看成是一个边长为$(a + b)$的大正方形,面积为
$(a + b)^2$
;也可以看成是由 2 个小正方形和 2 个小长方形组成的图形,面积为$a^2 + 2ab + b^2$
,则可得$(a + b)^2$
= $a^2 + 2ab + b^2$
.
(2)一般地,对于任意的$a$,$b$,由多项式乘多项式法则可以得到:$(a + b)^2 = (a + b)(a + b) =$
$a^2 + 2ab + b^2$
.2. 完全平方公式:$(a + b)^2 =$
$a^2 + 2ab + b^2$
;$(a - b)^2 =$$a^2 - 2ab + b^2$
.答案:1.(1)$(a + b)^2$ $a^2 + 2ab + b^2$ $(a + b)^2$ $a^2 + 2ab + b^2$
(2)$a^2 + 2ab + b^2$
2.$a^2 + 2ab + b^2$ $a^2 - 2ab + b^2$
(2)$a^2 + 2ab + b^2$
2.$a^2 + 2ab + b^2$ $a^2 - 2ab + b^2$
1. 计算$(-a - b)^2$的结果是(
A.$a^2 + b^2$
B.$a^2 - b^2$
C.$a^2 + 2ab + b^2$
D.$a^2 - 2ab + b^2$
C
)A.$a^2 + b^2$
B.$a^2 - b^2$
C.$a^2 + 2ab + b^2$
D.$a^2 - 2ab + b^2$
答案:1.C
解析:
$(-a - b)^2 = [-(a + b)]^2 = (a + b)^2 = a^2 + 2ab + b^2$,结果为选项C。
2. 计算$(x + 1)^2 + (x - 1)^2$的结果是
$2x^2 + 2$
.答案:2.$2x^2 + 2$
解析:
$(x + 1)^2 + (x - 1)^2$
$=x^2 + 2x + 1 + x^2 - 2x + 1$
$=2x^2 + 2$
$=x^2 + 2x + 1 + x^2 - 2x + 1$
$=2x^2 + 2$
3. 计算:
(1)$(2x + 5y)^2$;
(2)$(m - \frac{1}{2})^2$;
(3)$(-2t - 1)^2$;
(4)$(-cd + \frac{1}{2})^2$.
(1)$(2x + 5y)^2$;
(2)$(m - \frac{1}{2})^2$;
(3)$(-2t - 1)^2$;
(4)$(-cd + \frac{1}{2})^2$.
答案:3.解:(1)原式$= 4x^2 + 20xy + 25y^2$.
(2)原式$= m^2 - m + \frac{1}{4}$.
(3)原式$= 4t^2 + 4t + 1$.
(4)原式$= c^2d^2 - cd + \frac{1}{4}$.
(2)原式$= m^2 - m + \frac{1}{4}$.
(3)原式$= 4t^2 + 4t + 1$.
(4)原式$= c^2d^2 - cd + \frac{1}{4}$.
4. 用完全平方公式进行计算:
(1)$103^2$;
(2)$301^2$.
(1)$103^2$;
(2)$301^2$.
答案:4.解:(1)原式$= (100 + 3)^2 = 10000 + 600 + 9 = 10609$.
(2)原式$= (300 + 1)^2 = 90000 + 600 + 1 = 90601$.
(2)原式$= (300 + 1)^2 = 90000 + 600 + 1 = 90601$.
5. 已知$a + b = 8$,$ab = 6$. 求下列各式的值:
(1)$(a + b)^2$;
(2)$a^2 + b^2$.
(1)$(a + b)^2$;
(2)$a^2 + b^2$.
答案:5.解:(1)因为$a + b = 8$,
所以$(a + b)^2 = 8^2 = 64$.
(2)因为$a + b = 8$,$ab = 6$,
所以$a^2 + b^2 = (a + b)^2 - 2ab = 8^2 - 2×6 = 64 - 12 = 52$.
所以$(a + b)^2 = 8^2 = 64$.
(2)因为$a + b = 8$,$ab = 6$,
所以$a^2 + b^2 = (a + b)^2 - 2ab = 8^2 - 2×6 = 64 - 12 = 52$.