新知梳理
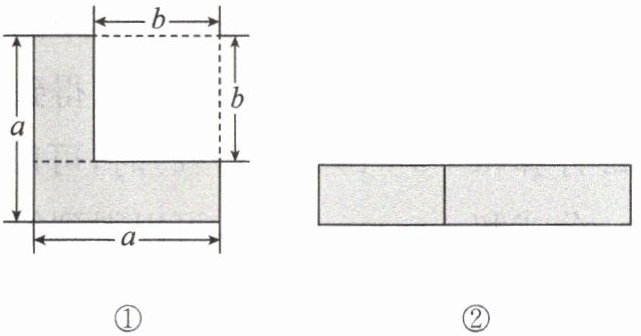
1. (1)如图①,在边长为 $a$ 的大正方形纸片上剪去一个边长为 $b(b < a)$ 的小正方形,则阴影部分的面积为
(2)一般地,对于任意的 $a,b$,由多项式乘多项式法则可以得到 $(a + b)(a - b)=$
2. 平方差公式:$(a + b)(a - b)=$
1. (1)如图①,在边长为 $a$ 的大正方形纸片上剪去一个边长为 $b(b < a)$ 的小正方形,则阴影部分的面积为
$a^{2}-b^{2}$
;也可以由图①剪拼成图②,得到一个长为$(a+b)$
,宽为$(a-b)$
的长方形,面积为$(a+b)(a-b)$
,则可得$(a+b)(a-b)$
=$a^{2}-b^{2}$
.
(2)一般地,对于任意的 $a,b$,由多项式乘多项式法则可以得到 $(a + b)(a - b)=$
$a^{2}-b^{2}$
.2. 平方差公式:$(a + b)(a - b)=$
$a^{2}-b^{2}$
.答案:1.(1)$a^{2}-b^{2}$ $(a+b)$ $(a-b)$ $(a+b)(a-b)$ $(a+b)(a-b)$ $a^{2}-b^{2}$ (2)$a^{2}-b^{2}$
2.$a^{2}-b^{2}$
2.$a^{2}-b^{2}$
1. 若$ (2a + 3b)( ) ) = 4a^{2}-9b^{2}$,则括号内应填的代数式是(
A.-2a - 3b
B.2a + 3b
C.2a - 3b
D.3b - 2a
C
)A.-2a - 3b
B.2a + 3b
C.2a - 3b
D.3b - 2a
答案:1.C
解析:
因为$4a^{2}-9b^{2}=(2a)^{2}-(3b)^{2}=(2a + 3b)(2a - 3b)$,所以括号内应填的代数式是$2a - 3b$。
C
C
2. 将 $2001×1999$ 变形正确的是(
A.$2000^{2}-1$
B.$2000^{2}+1$
C.$2000^{2}+2×2000 + 1$
D.$2000^{2}-2×2000 + 1$
A
)A.$2000^{2}-1$
B.$2000^{2}+1$
C.$2000^{2}+2×2000 + 1$
D.$2000^{2}-2×2000 + 1$
答案:2.A
解析:
$2001×1999=(2000 + 1)(2000 - 1)=2000^{2}-1^{2}=2000^{2}-1$,A
3. 如果一个长方形的长是 $(x + 3y)$ 米,宽是 $(x - 3y)$ 米,那么该长方形的面积是
$(x^{2}-9y^{2})$
平方米.答案:3.$(x^{2}-9y^{2})$
4. 化简:
(1) $(a + 2b)(a + 2b)$;
(2) $(a + 2b)(a - 2b)$;
(3) $(a + 2b)(-a + 2b)$;
(4) $(a + 2b)(-a - 2b)$.
(1) $(a + 2b)(a + 2b)$;
(2) $(a + 2b)(a - 2b)$;
(3) $(a + 2b)(-a + 2b)$;
(4) $(a + 2b)(-a - 2b)$.
答案:4.解:(1)原式$=a^{2}+4ab+4b^{2}$.
(2)原式$=a^{2}-4b^{2}$.
(3)原式$=4b^{2}-a^{2}$.
(4)原式$=-(a+2b)(a+2b)=-a^{2}-4ab-4b^{2}$.
(2)原式$=a^{2}-4b^{2}$.
(3)原式$=4b^{2}-a^{2}$.
(4)原式$=-(a+2b)(a+2b)=-a^{2}-4ab-4b^{2}$.
5. 计算:$29.3^{2}-28.3^{2}$.
答案:5.解:原式$=(29.3+28.3)×(29.3-28.3)=57.6×1=57.6$.