新知梳理
1. 一般地,在平面内,若一个图形是由另一个图形绕某个点旋转
2. 成中心对称的两个图形中,对应点的连线经过
3. 把一个图形绕某一点旋转
1. 一般地,在平面内,若一个图形是由另一个图形绕某个点旋转
180°
得到的,则称这两个图形成中心对称
,这个点叫作对称中心
,两个对称图形上的对应点叫作对称点
。2. 成中心对称的两个图形中,对应点的连线经过
对称中心
,且被对称中心平分
。3. 把一个图形绕某一点旋转
180°
,如果旋转后的图形就是其本身,那么这个图形叫作中心对称图形
,这个点就是它的对称中心
。答案:1. 180° 成中心对称 对称中心 对称点
2. 对称中心 平分
3. 180° 中心对称图形 对称中心
2. 对称中心 平分
3. 180° 中心对称图形 对称中心
1. 下列图形是中心对称图形的是(
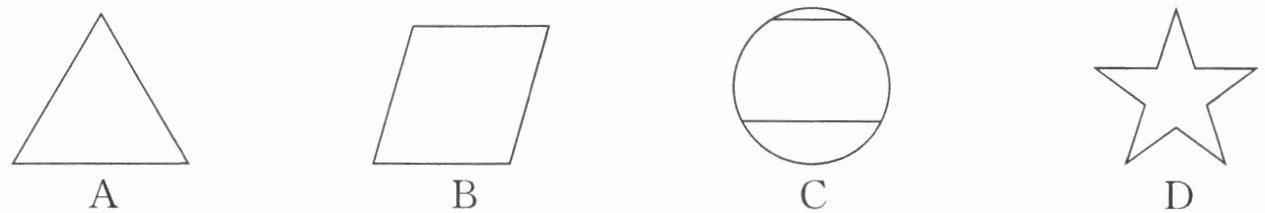
B
)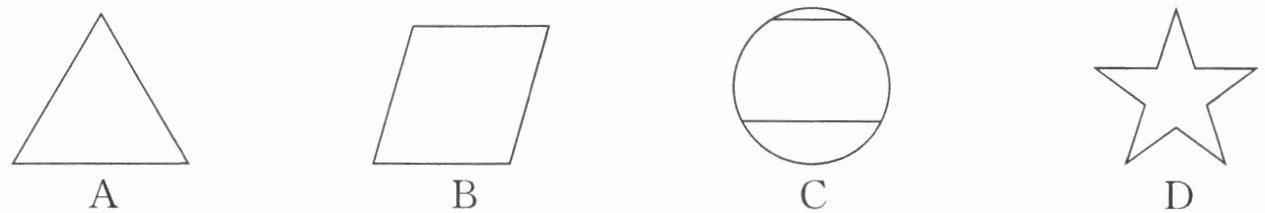
答案:1. B
2. 如图是中心对称图形,则对称中心是(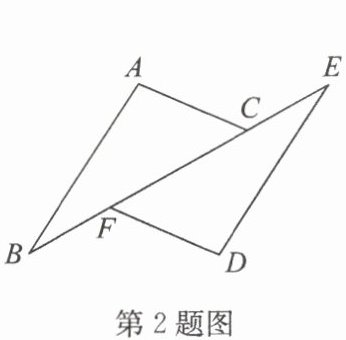
A.点 $ C $
B.点 $ D $
C.线段 $ BC $ 的中点
D.线段 $ FC $ 的中点
D
)
A.点 $ C $
B.点 $ D $
C.线段 $ BC $ 的中点
D.线段 $ FC $ 的中点
答案:2. D
解析:
证明:因为图形是中心对称图形,所以对称中心是对应点连线的中点。观察图形可知,点F与点C是对应点,因此对称中心是线段FC的中点。
D
D
3. 如图,$ △ ABC $ 与 $ △ DEF $ 关于点 $ O $ 成中心对称. 下列结论不一定正确的是(
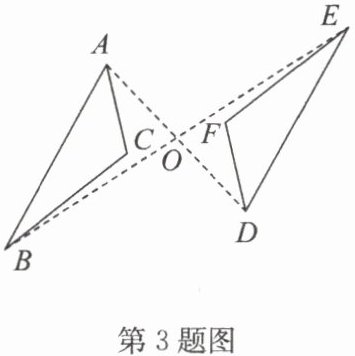
A.$ AB // DE $
B.$ AO = DO $
C.$ AD ⊥ BE $
D.$ ∠ CAO = ∠ FDO $
C
)
A.$ AB // DE $
B.$ AO = DO $
C.$ AD ⊥ BE $
D.$ ∠ CAO = ∠ FDO $
答案:3. C
解析:
证明:
∵△ABC与△DEF关于点O成中心对称,
∴点A与点D、点B与点E、点C与点F关于点O对称,
∴AO=DO,BO=EO,CO=FO,∠AOB=∠DOE,∠AOC=∠DOF,
∴△AOB≌△DOE,△AOC≌△DOF,
∴∠OAB=∠ODE,∠CAO=∠FDO,
∴AB//DE,
故A、B、D正确,C不一定正确。
答案:C
∵△ABC与△DEF关于点O成中心对称,
∴点A与点D、点B与点E、点C与点F关于点O对称,
∴AO=DO,BO=EO,CO=FO,∠AOB=∠DOE,∠AOC=∠DOF,
∴△AOB≌△DOE,△AOC≌△DOF,
∴∠OAB=∠ODE,∠CAO=∠FDO,
∴AB//DE,
故A、B、D正确,C不一定正确。
答案:C
4. 如图,已知 $ △ ABC $ 和点 $ O $,请作出与 $ △ ABC $ 关于点 $ O $ 成中心对称的三角形.(尺规作图,保留痕迹,不写作法)
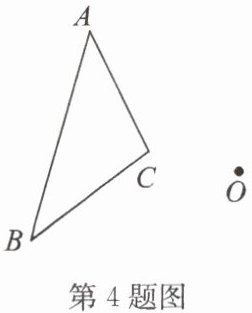
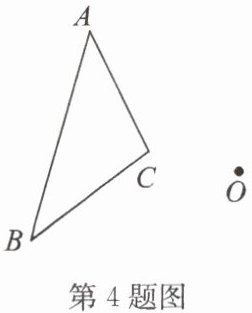
答案:
4. 解:如答图所示,△A′B′C′即为所求.
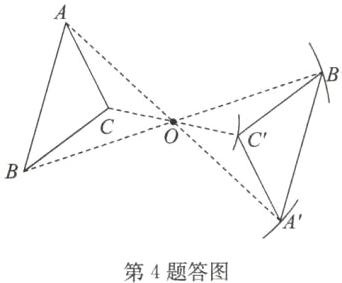
4. 解:如答图所示,△A′B′C′即为所求.
