新知梳理
1. 根据实物示意图,可以从中获取数量关系,进而挖掘出隐含在其中的
2. 利用示意图是用二元一次方程组解决问题的一个重要手段,画示意图,通常是画
1. 根据实物示意图,可以从中获取数量关系,进而挖掘出隐含在其中的
两
个相等关系式,并利用所设的未知数,建立方程组解决问题.2. 利用示意图是用二元一次方程组解决问题的一个重要手段,画示意图,通常是画
线段
图或曲线图,用线段
或曲线段的长度表示某些量,并根据这些线段或曲线段的长度
关系列出方程组.尤其是许多行程问题中的数量关系可以简明地用示意
图表示.答案:1. 两 2. 线段 线段 长度 示意
1. 甲、乙两人合作加工一批三条腿和四条腿两种型号的凳子(如图所示).加工完后,甲说:“我做了 40 条凳子腿.”乙说:“我做了 12 个凳子面.”求三条腿的凳子和四条腿的凳子各有多少个.
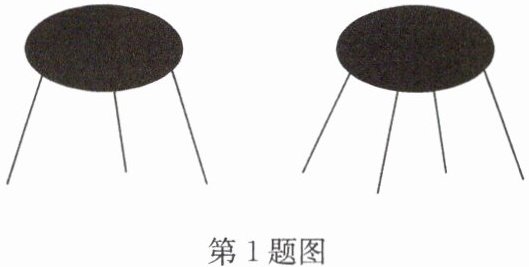

答案:1. 解:设三条腿的凳子有 x 个,四条腿的凳子有 y 个,
根据题意,得 $\begin{cases}x + y = 12,\\3x + 4y = 40,\end{cases}$ 解得 $\begin{cases}x = 8,\\y = 4.\end{cases}$
答:三条腿的凳子有 8 个,四条腿的凳子有 4 个.
根据题意,得 $\begin{cases}x + y = 12,\\3x + 4y = 40,\end{cases}$ 解得 $\begin{cases}x = 8,\\y = 4.\end{cases}$
答:三条腿的凳子有 8 个,四条腿的凳子有 4 个.
2. 把 10 个相同的小长方形拼接成如图所示的一个大长方形(尺寸如图所示),求大长方形的面积.
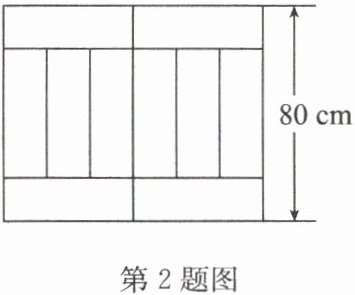

答案:2. 解:设一个小长方形的长为 x cm,宽为 y cm,
根据题意,得 $\begin{cases}x = 3y,\\x + 2y = 80,\end{cases}$ 解得 $\begin{cases}x = 48,\\y = 16.\end{cases}$
所以大长方形的面积为 $48×2×80 = 7680(cm^{2})$.
答:大长方形的面积为 $7680 cm^{2}$.
根据题意,得 $\begin{cases}x = 3y,\\x + 2y = 80,\end{cases}$ 解得 $\begin{cases}x = 48,\\y = 16.\end{cases}$
所以大长方形的面积为 $48×2×80 = 7680(cm^{2})$.
答:大长方形的面积为 $7680 cm^{2}$.
3. 某学校组织学生举行“远足研学”活动,先以每小时 6 千米的速度走平路,后又以每小时 3 千米的速度上坡,共用了 3 小时;原路返回时,以每小时 5 千米的速度下坡,又以每小时 4 千米的速度走平路,共用了 4 小时.求平路和坡路各有多少千米.
答案:3. 解:设平路有 x 千米,坡路有 y 千米,
根据题意,得 $\begin{cases}\dfrac{x}{6} + \dfrac{y}{3} = 3,\\\dfrac{x}{4} + \dfrac{y}{5} = 4,\end{cases}$ 解得 $\begin{cases}x = \dfrac{44}{3},\\y = \dfrac{5}{3}.\end{cases}$
答:平路有 $\dfrac{44}{3}$ 千米,坡路有 $\dfrac{5}{3}$ 千米.
根据题意,得 $\begin{cases}\dfrac{x}{6} + \dfrac{y}{3} = 3,\\\dfrac{x}{4} + \dfrac{y}{5} = 4,\end{cases}$ 解得 $\begin{cases}x = \dfrac{44}{3},\\y = \dfrac{5}{3}.\end{cases}$
答:平路有 $\dfrac{44}{3}$ 千米,坡路有 $\dfrac{5}{3}$ 千米.