新知梳理
1. 解一元一次不等式的一般步骤与解一元一次方程类似:去分母、
2. 解一元一次不等式时,特别要注意:在不等式两边都乘(或除以)同一个负数时,根据不等式的基本性质
1. 解一元一次不等式的一般步骤与解一元一次方程类似:去分母、
去括号
、移项、合并同类项、将未知数的系数化为1
.2. 解一元一次不等式时,特别要注意:在不等式两边都乘(或除以)同一个负数时,根据不等式的基本性质
2
,不等号的方向必须改变
.答案:1.去括号 1 2.2 改变
解析:
1. 去括号;1
2. 2;改变
2. 2;改变
1. 解下列一元一次不等式:
(1) $ 3(x - 2) - x ≤ 4 $;
(2) $ 2(3x - 4) ≤ x - 2(1 - x) $;
(3) $ \frac{x - 1}{3} > x - 3 $;
(4) $ \frac{4 + x}{3} - 1 < \frac{x}{2} $.
(1) $ 3(x - 2) - x ≤ 4 $;
(2) $ 2(3x - 4) ≤ x - 2(1 - x) $;
(3) $ \frac{x - 1}{3} > x - 3 $;
(4) $ \frac{4 + x}{3} - 1 < \frac{x}{2} $.
答案:1.解:(1)去括号,得 $ 3x - 6 - x ≤ 4 $,
移项、合并同类项,得 $ 2x ≤ 10 $,
两边都除以2,得 $ x ≤ 5 $。
(2)去括号,得 $ 6x - 8 ≤ x - 2 + 2x $,
移项,得 $ 6x - x - 2x ≤ - 2 + 8 $,
合并同类项,得 $ 3x ≤ 6 $,
两边都除以3,得 $ x ≤ 2 $。
(3)去分母,得 $ x - 1 > 3(x - 3) $,
去括号,得 $ x - 1 > 3x - 9 $,
移项、合并同类项,得 $ - 2x > - 8 $,
两边都除以 $ - 2 $,得 $ x < 4 $。
(4)去分母,得 $ 2(4 + x) - 6 < 3x $,
去括号,得 $ 8 + 2x - 6 < 3x $,
移项、合并同类项,得 $ - x < - 2 $,
两边都除以 $ - 1 $,得 $ x > 2 $。
移项、合并同类项,得 $ 2x ≤ 10 $,
两边都除以2,得 $ x ≤ 5 $。
(2)去括号,得 $ 6x - 8 ≤ x - 2 + 2x $,
移项,得 $ 6x - x - 2x ≤ - 2 + 8 $,
合并同类项,得 $ 3x ≤ 6 $,
两边都除以3,得 $ x ≤ 2 $。
(3)去分母,得 $ x - 1 > 3(x - 3) $,
去括号,得 $ x - 1 > 3x - 9 $,
移项、合并同类项,得 $ - 2x > - 8 $,
两边都除以 $ - 2 $,得 $ x < 4 $。
(4)去分母,得 $ 2(4 + x) - 6 < 3x $,
去括号,得 $ 8 + 2x - 6 < 3x $,
移项、合并同类项,得 $ - x < - 2 $,
两边都除以 $ - 1 $,得 $ x > 2 $。
2. 解下列不等式,并把解集表示在数轴上:
(1) $ 5(x - 3) - 2(x - 4) > 2 $;
(2) $ \frac{x + 2}{5} - \frac{x - 2}{2} ≥ 2 $.
(1) $ 5(x - 3) - 2(x - 4) > 2 $;
(2) $ \frac{x + 2}{5} - \frac{x - 2}{2} ≥ 2 $.
答案:
2.解:(1)去括号,得 $ 5x - 15 - 2x + 8 > 2 $,
移项、合并同类项,得 $ 3x > 9 $,
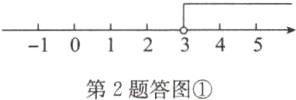
两边都除以3,得 $ x > 3 $。
解集在数轴上表示如答图①所示。
(2)去分母,得 $ 2(x + 2) - 5(x - 2) ≥ 20 $,
去括号,得 $ 2x + 4 - 5x + 10 ≥ 20 $,
移项,得 $ 2x - 5x ≥ 20 - 4 - 10 $,
合并同类项,得 $ - 3x ≥ 6 $,
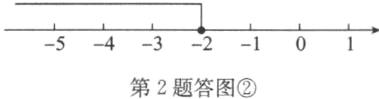
两边都除以 $ - 3 $,得 $ x ≤ - 2 $。
解集在数轴上表示如答图②所示。
2.解:(1)去括号,得 $ 5x - 15 - 2x + 8 > 2 $,
移项、合并同类项,得 $ 3x > 9 $,
两边都除以3,得 $ x > 3 $。
解集在数轴上表示如答图①所示。

(2)去分母,得 $ 2(x + 2) - 5(x - 2) ≥ 20 $,
去括号,得 $ 2x + 4 - 5x + 10 ≥ 20 $,
移项,得 $ 2x - 5x ≥ 20 - 4 - 10 $,
合并同类项,得 $ - 3x ≥ 6 $,
两边都除以 $ - 3 $,得 $ x ≤ - 2 $。
解集在数轴上表示如答图②所示。

3. 解不等式 $ x - 1 < \frac{2x - 1}{3} $,并写出它的所有非负整数解.
答案:3.解:去分母,得 $ 3x - 3 < 2x - 1 $,
移项、合并同类项,得 $ x < 2 $。
所以不等式的所有非负整数解为0,1。
移项、合并同类项,得 $ x < 2 $。
所以不等式的所有非负整数解为0,1。