新知梳理
从命题的条件出发,根据一些已知的
从命题的条件出发,根据一些已知的
事实
(如概念的定义
,基本性质,真命题等),用“因为……,所以……”的形式一步一步推出命题的结论,从而确定这个命题为真命题的过程称为证明.答案:新知梳理
事实 定义
事实 定义
1. 下列语句:①数轴上,右边的数总大于左边的数;②末尾的数是 0 或 5 的整数一定能被 5 整除;③过一点有且只有一条直线与已知直线平行;④垂线段最短. 其中是假命题的是
③
.(填序号)答案:1. ③
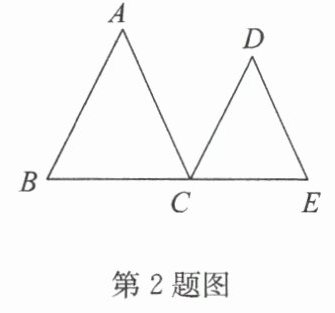
2. 已知:如图,$AB// CD$,$∠ A=∠ D$,试说明:$AC// DE$. 下面是彬彬同学的推理,请你将他的推理过程补充完整.
解:因为 $AB// CD$(已知),
所以 $∠ A=∠$
又因为 $∠ A=∠ D$(
所以 $∠$
所以 $AC// DE$(
解:因为 $AB// CD$(已知),
所以 $∠ A=∠$
ACD
(两直线平行,内错角相等
).又因为 $∠ A=∠ D$(
已知
),所以 $∠$
ACD
$=∠$D
(等量代换),所以 $AC// DE$(
内错角相等,两直线平行
).
答案:2. ACD 两直线平行,内错角相等 已知 ACD D 内错角相等,两直线平行
解析:
解:因为 $AB// CD$(已知),
所以 $∠ A=∠ACD$(两直线平行,内错角相等).
又因为 $∠ A=∠ D$(已知),
所以 $∠ACD=∠D$(等量代换),
所以 $AC// DE$(内错角相等,两直线平行).
所以 $∠ A=∠ACD$(两直线平行,内错角相等).
又因为 $∠ A=∠ D$(已知),
所以 $∠ACD=∠D$(等量代换),
所以 $AC// DE$(内错角相等,两直线平行).
3.(教材例题变式)已知 $a$,$b$ 都是奇数,求证:$a + b$ 是偶数.
答案:3. 证明:因为 a,b 都是奇数,
所以可设 a = 2m + 1,b = 2n + 1(m,n 是整数),
所以 a + b = 2m + 1 + 2n + 1 = 2(m + n + 1),
所以 a + b 是偶数。
所以可设 a = 2m + 1,b = 2n + 1(m,n 是整数),
所以 a + b = 2m + 1 + 2n + 1 = 2(m + n + 1),
所以 a + b 是偶数。
4. 如图,$AB// CD$,$∠ B = 80^{\circ}$,$∠ D = 100^{\circ}$,求证:$BC// ED$.
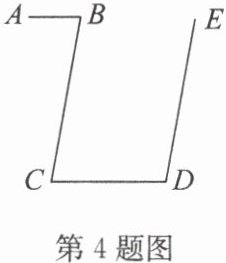

答案:4. 证明:因为 AB//CD,∠B = 80°(已知),
所以 ∠C = ∠B = 80°(两直线平行,内错角相等)。
因为 ∠D = 100°(已知),
所以 ∠C + ∠D = 80° + 100° = 180°(等式的性质),
所以 BC//ED(同旁内角互补,两直线平行)。
所以 ∠C = ∠B = 80°(两直线平行,内错角相等)。
因为 ∠D = 100°(已知),
所以 ∠C + ∠D = 80° + 100° = 180°(等式的性质),
所以 BC//ED(同旁内角互补,两直线平行)。