新知梳理
1. 在证明过程中,为了书写方便,可以用“∵”表示“
2. 证明与图形有关的命题,一般有以下步骤:(1)根据题意,画出
1. 在证明过程中,为了书写方便,可以用“∵”表示“
因为
”,用“∴”表示“所以
”.2. 证明与图形有关的命题,一般有以下步骤:(1)根据题意,画出
图形
;(2)根据命题的条件、结论,结合图形,写出已知、求证
;(3)写出证明过程.答案:1.因为 所以
2.(1)图形 (2)已知、求证
2.(1)图形 (2)已知、求证
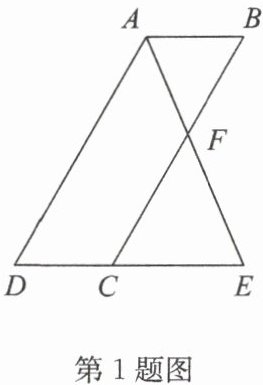
1. 如图,∠B = ∠D,∠BAE = ∠E.求证:∠AFC + ∠DAE = 180°.

答案:1.证明:因为∠BAE=∠E,
所以AB//DE(内错角相等,两直线平行),
所以∠B=∠BCE(两直线平行,内错角相等)。
因为∠B=∠D,
所以∠D=∠BCE(等量代换),
所以AD//BC(同位角相等,两直线平行),
所以∠AFC + ∠DAE = 180°(两直线平行,同旁内角互补)。
所以AB//DE(内错角相等,两直线平行),
所以∠B=∠BCE(两直线平行,内错角相等)。
因为∠B=∠D,
所以∠D=∠BCE(等量代换),
所以AD//BC(同位角相等,两直线平行),
所以∠AFC + ∠DAE = 180°(两直线平行,同旁内角互补)。
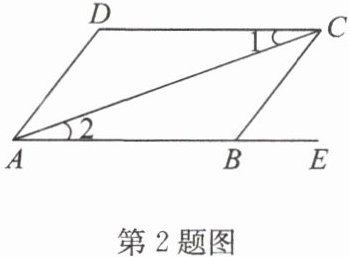
2. (教材习题变式)在四边形ABCD中,∠1 = ∠2,∠DAB = ∠CBE,求证:∠D = ∠ABC.

答案:2.证明:因为∠1=∠2(已知),
所以AB//CD(内错角相等,两直线平行),
所以∠D + ∠DAB = 180°(两直线平行,同旁内角互补)。
因为∠DAB = ∠CBE(已知),
所以∠D + ∠CBE = 180°(等量代换)。
又因为∠ABC + ∠CBE = 180°(平角定义),
所以∠D = ∠ABC(同角的补角相等)。
所以AB//CD(内错角相等,两直线平行),
所以∠D + ∠DAB = 180°(两直线平行,同旁内角互补)。
因为∠DAB = ∠CBE(已知),
所以∠D + ∠CBE = 180°(等量代换)。
又因为∠ABC + ∠CBE = 180°(平角定义),
所以∠D = ∠ABC(同角的补角相等)。
3. 证明:若两直线平行,则同位角的角平分线平行.(画出图形,写出已知、求证,并证明)
答案:
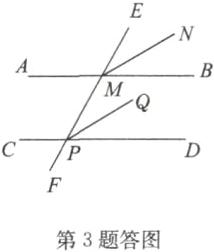
3.解:已知:如答图,AB//CD,直线EF与AB相交于点M,与CD相交于点P,且MN平分∠BME,PQ平分∠DPE;
求证:MN//PQ.
证明:因为AB//CD,所以∠BME = ∠DPE;
因为MN平分∠BME,PQ平分∠DPE,
所以∠EMN = $\frac{1}{2}$∠BME、∠EPQ = $\frac{1}{2}$∠DPE,
所以∠EMN = ∠EPQ,所以MN//PQ
3.解:已知:如答图,AB//CD,直线EF与AB相交于点M,与CD相交于点P,且MN平分∠BME,PQ平分∠DPE;
求证:MN//PQ.
证明:因为AB//CD,所以∠BME = ∠DPE;
因为MN平分∠BME,PQ平分∠DPE,
所以∠EMN = $\frac{1}{2}$∠BME、∠EPQ = $\frac{1}{2}$∠DPE,
所以∠EMN = ∠EPQ,所以MN//PQ
