新知梳理
1. 一般情况下,数学中把一些
2. (1)三角形的内角和定理:
3. 由一个定理直接推出的重要结论,一般叫作这个定理的
1. 一般情况下,数学中把一些
基本的
、重要的
真命题叫作定理. 定理可以作为证明后续命题的依据.2. (1)三角形的内角和定理:
三角形三个内角的和等于180°
;(2)三角形的外角等于与它不相邻
的两个内角的和.3. 由一个定理直接推出的重要结论,一般叫作这个定理的
推论
. 它和定理一样,也可以作为后续证明的依据.答案:1.基本的 重要的
2.(1)三角形三个内角的和等于180°
(2)与它不相邻
3.推论
2.(1)三角形三个内角的和等于180°
(2)与它不相邻
3.推论
1. 下列关于三角形的外角和的叙述,正确的是(
A.三角形的外角和等于 $180^{\circ}$
B.三角形的外角和就是所有外角的和
C.三角形的内角和等于其外角和
D.三角形的外角和等于 $360^{\circ}$
D
)A.三角形的外角和等于 $180^{\circ}$
B.三角形的外角和就是所有外角的和
C.三角形的内角和等于其外角和
D.三角形的外角和等于 $360^{\circ}$
答案:1.D
2. 如图,直线 $a// b$,$∠ 1 = 63^{\circ}$,$∠ B = 45^{\circ}$,则$∠ 2$的度数为(
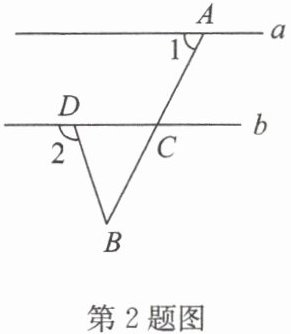
A.$105^{\circ}$
B.$108^{\circ}$
C.$117^{\circ}$
D.$135^{\circ}$
B
)
A.$105^{\circ}$
B.$108^{\circ}$
C.$117^{\circ}$
D.$135^{\circ}$
答案:2.B
3. 如图,$AB// CD$,$∠ B = 145^{\circ}$,$∠ DFE = 40^{\circ}$,则$∠ BEF$的度数为(
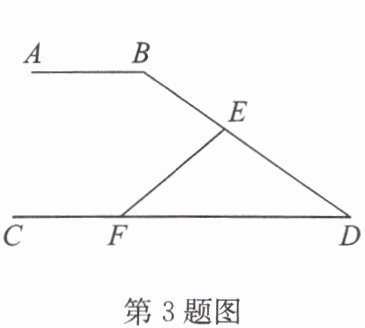
A.$40^{\circ}$
B.$50^{\circ}$
C.$75^{\circ}$
D.$70^{\circ}$
C
)
A.$40^{\circ}$
B.$50^{\circ}$
C.$75^{\circ}$
D.$70^{\circ}$
答案:3.C
解析:
证明:延长BE交CD于点G。
∵AB//CD,∠B=145°,
∴∠BGD=180°-∠B=180°-145°=35°。
∵∠DFE=40°,∠DFE是△EFG的外角,
∴∠BEF=∠BGD+∠DFE=35°+40°=75°。
答案:C
∵AB//CD,∠B=145°,
∴∠BGD=180°-∠B=180°-145°=35°。
∵∠DFE=40°,∠DFE是△EFG的外角,
∴∠BEF=∠BGD+∠DFE=35°+40°=75°。
答案:C
4. 如图,在$△ ABC$中,$∠ B = 68^{\circ}$,$∠ C = 32^{\circ}$,$AD$平分$∠ BAC$,$AE⊥ BC$于点$E$,则$∠ EAD$的度数是(
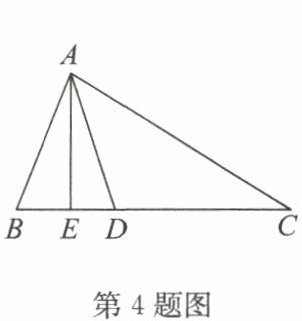
A.$22^{\circ}$
B.$20^{\circ}$
C.$18^{\circ}$
D.$16^{\circ}$
C
)
A.$22^{\circ}$
B.$20^{\circ}$
C.$18^{\circ}$
D.$16^{\circ}$
答案:4.C
解析:
解:在$△ ABC$中,$∠ BAC=180^{\circ}-∠ B-∠ C=180^{\circ}-68^{\circ}-32^{\circ}=80^{\circ}$。
因为$AD$平分$∠ BAC$,所以$∠ BAD=\frac{1}{2}∠ BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$。
因为$AE⊥ BC$,所以$∠ AEB=90^{\circ}$,在$△ ABE$中,$∠ BAE=90^{\circ}-∠ B=90^{\circ}-68^{\circ}=22^{\circ}$。
则$∠ EAD=∠ BAD-∠ BAE=40^{\circ}-22^{\circ}=18^{\circ}$。
答案:C
因为$AD$平分$∠ BAC$,所以$∠ BAD=\frac{1}{2}∠ BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$。
因为$AE⊥ BC$,所以$∠ AEB=90^{\circ}$,在$△ ABE$中,$∠ BAE=90^{\circ}-∠ B=90^{\circ}-68^{\circ}=22^{\circ}$。
则$∠ EAD=∠ BAD-∠ BAE=40^{\circ}-22^{\circ}=18^{\circ}$。
答案:C
5. (教材习题变式)写出“两个锐角互余的三角形是直角三角形”的逆命题,判断真假并给出证明.
答案:
5.解:原命题的逆命题:直角三角形的两个锐角互余,真命题
如答图,在△ABC中,∠C=90°,求证:∠A与∠B互余

证明:因为在△ABC中,∠A+∠B+∠C=180°(三角形的内角和定理),
又因为∠C=90°(已知),
所以∠A+∠B=180°−∠C=180°−90°=90°,
所以∠A与∠B互余(余角定义)
5.解:原命题的逆命题:直角三角形的两个锐角互余,真命题
如答图,在△ABC中,∠C=90°,求证:∠A与∠B互余

证明:因为在△ABC中,∠A+∠B+∠C=180°(三角形的内角和定理),
又因为∠C=90°(已知),
所以∠A+∠B=180°−∠C=180°−90°=90°,
所以∠A与∠B互余(余角定义)