新知梳理
1. 多边形内角和定理:n 边形的内角和等于
2. 多边形外角和定理:多边形的外角和等于
1. 多边形内角和定理:n 边形的内角和等于
$(n - 2) · 180^{\circ}$
。2. 多边形外角和定理:多边形的外角和等于
$360^{\circ}$
。答案:1. $(n - 2) · 180^{\circ}$ 2. $360^{\circ}$
1. 一个八边形的内角和是(
A.$1080^{\circ}$
B.$900^{\circ}$
C.$720^{\circ}$
D.$540^{\circ}$
A
)A.$1080^{\circ}$
B.$900^{\circ}$
C.$720^{\circ}$
D.$540^{\circ}$
答案:1. A
2. 十二边形的外角和为(
A.$30^{\circ}$
B.$150^{\circ}$
C.$360^{\circ}$
D.$1800^{\circ}$
C
)A.$30^{\circ}$
B.$150^{\circ}$
C.$360^{\circ}$
D.$1800^{\circ}$
答案:2. C
3. 一个多边形的每个外角均为 $72^{\circ}$,则这个多边形是(
A.八边形
B.七边形
C.六边形
D.五边形
D
)A.八边形
B.七边形
C.六边形
D.五边形
答案:3. D
解析:
因为多边形的外角和为$360^{\circ}$,每个外角均为$72^{\circ}$,所以这个多边形的边数为$360^{\circ}÷72^{\circ}=5$。
D
D
4. 如果十边形的各个内角都相等,那么它的一个内角是
$144^{\circ}$
。答案:4. $144^{\circ}$
5. n 边形的每一个外角都为 $30^{\circ}$,则它的对角线条数为
54
。答案:5. 54
解析:
因为多边形的外角和为$360^{\circ}$,每一个外角都为$30^{\circ}$,所以边数$n = \frac{360^{\circ}}{30^{\circ}} = 12$。
对角线条数公式为$\frac{n(n - 3)}{2}$,将$n = 12$代入可得:$\frac{12×(12 - 3)}{2} = \frac{12×9}{2} = 54$。
54
对角线条数公式为$\frac{n(n - 3)}{2}$,将$n = 12$代入可得:$\frac{12×(12 - 3)}{2} = \frac{12×9}{2} = 54$。
54
6. 如果一个多边形的内角和与外角和之比是 $13:2$,求这个多边形的边数。
答案:6. 解:设这个多边形的边数为 $n$,
根据题意,得 $(n - 2) · 180^{\circ} = 360^{\circ} × \frac{13}{2}$,解得 $n = 15$。
答:这个多边形的边数为 15。
根据题意,得 $(n - 2) · 180^{\circ} = 360^{\circ} × \frac{13}{2}$,解得 $n = 15$。
答:这个多边形的边数为 15。
7. (教材例题变式)如图,小明从点 A 出发,前进 10 m 后向右转 $x^{\circ}$,再前进 10 m 后又向右转 $x^{\circ}$,这样一直下去,直到他第一次回到出发点 A 为止,他所走的路径构成了一个多边形,他一共走了 360 m,求 x 的值,并判断这个多边形的边数。
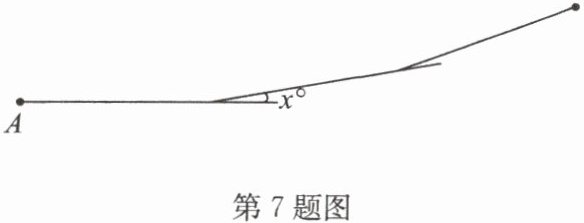

答案:7. 解:根据题意,得 $\frac{360}{10}x = 360$,解得 $x = 10$。
该多边形的边数为 $\frac{360}{10} = 36$。
答:$x$ 的值为 10,这个多边形的边数是 36。
该多边形的边数为 $\frac{360}{10} = 36$。
答:$x$ 的值为 10,这个多边形的边数是 36。