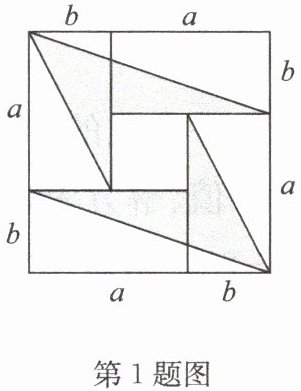
1. 用 4 张长为a,宽为b的长方形纸片,按如图的方式拼成一个边长为$(a+b)$的正方形,图中空白部分的面积为$S_{1}$,阴影部分的面积为$S_{2}$. 若$S_{1}=2S_{2}$,则a,b之间存在的数量关系是(
A.$a=1.5b$
B.$a=2b$
C.$a=2.5b$
D.$a=3b$
B
)
A.$a=1.5b$
B.$a=2b$
C.$a=2.5b$
D.$a=3b$
答案:1. B 点拨: 由题图可知空白部分的面积 $ S_{1}=2 × \frac{1}{2} b(a + b)+2 × \frac{1}{2} a b+(a - b)^{2}=a^{2}+2 b^{2} $. 因为 $ S_{2}=(a + b)^{2}-S_{1}=2 a b - b^{2} $, 且 $ S_{1}=2 S_{2} $, 所以 $ a^{2}+2 b^{2}=2(2 a b - b^{2}) $, 整理, 得 $ (a - 2 b)^{2}=0 $, 所以 $ a = 2 b $.
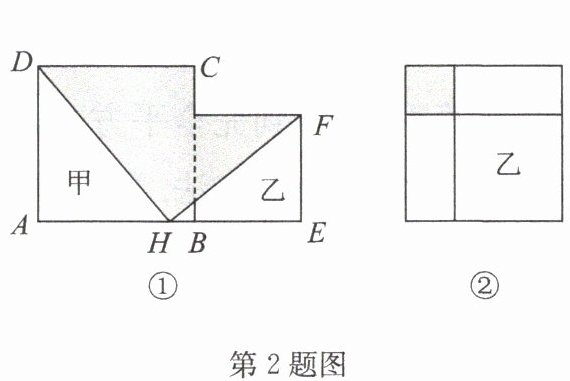
2. 现有甲、乙两张正方形纸片,将甲、乙并列放置后得到图①,H 为 AE 的中点,连接DH,FH. 将乙纸片放到甲纸片的内部得到图②. 已知甲、乙两个正方形边长之和为 8,图②中阴影部分的面积为 6,则图①中阴影部分的面积为
19
.
答案:2. 19 点拨: 设甲正方形的边长为 $ a $, 乙正方形的边长为 $ b $, 根据题意, 得 $ \begin{cases}a + b = 8, \\ (a - b)^{2}=6,\end{cases} $ 所以 $ (a + b)^{2}=64 $, 所以 $ 2(a^{2}+b^{2})=(a + b)^{2}+(a - b)^{2}=70 $, 所以 $ a^{2}+b^{2}=35 $. 因为 $ H $ 为 $ AE $ 的中点, 所以 $ AH = EH = \frac{1}{2}(AB + BE)=\frac{1}{2}(a + b)=4 $, 所以 $ S_{△ AHD}=\frac{1}{2} AD · AH=\frac{1}{2} a × 4=2 a $, $ S_{△ EFH}=\frac{1}{2} EF · HE=\frac{1}{2} b × 4=2 b $, 所以 $ S_{\mathrm{阴影}}=a^{2}+b^{2}-2 a - 2 b=a^{2}+b^{2}-2(a + b)=19 $.
解析:
设甲正方形的边长为$a$,乙正方形的边长为$b$。
由题意得:
$\begin{cases}a + b = 8 \\(a - b)^2 = 6\end{cases}$
因为$(a + b)^2 = 64$,所以$2(a^2 + b^2) = (a + b)^2 + (a - b)^2 = 64 + 6 = 70$,则$a^2 + b^2 = 35$。
因为$H$为$AE$的中点,所以$AH = EH = \frac{1}{2}(a + b) = 4$。
$S_{△ AHD} = \frac{1}{2} × AD × AH = \frac{1}{2} × a × 4 = 2a$,$S_{△ EFH} = \frac{1}{2} × EF × HE = \frac{1}{2} × b × 4 = 2b$。
所以图①中阴影部分的面积为:
$a^2 + b^2 - 2a - 2b = 35 - 2(a + b) = 35 - 2 × 8 = 19$
19
由题意得:
$\begin{cases}a + b = 8 \\(a - b)^2 = 6\end{cases}$
因为$(a + b)^2 = 64$,所以$2(a^2 + b^2) = (a + b)^2 + (a - b)^2 = 64 + 6 = 70$,则$a^2 + b^2 = 35$。
因为$H$为$AE$的中点,所以$AH = EH = \frac{1}{2}(a + b) = 4$。
$S_{△ AHD} = \frac{1}{2} × AD × AH = \frac{1}{2} × a × 4 = 2a$,$S_{△ EFH} = \frac{1}{2} × EF × HE = \frac{1}{2} × b × 4 = 2b$。
所以图①中阴影部分的面积为:
$a^2 + b^2 - 2a - 2b = 35 - 2(a + b) = 35 - 2 × 8 = 19$
19
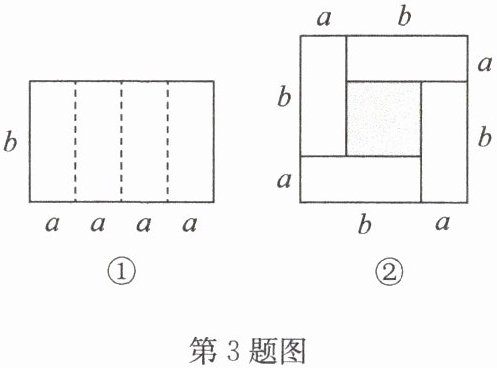
3. 如图①是长为4a,宽为b的长方形纸片,沿图中虚线用剪刀平均裁成四块小长方形,然后将四块小长方形拼成一个“回形”正方形,如图②.
(1)观察图②,请写出$(a+b)^{2},(a-b)^{2},ab$之间的等量关系是
(2)根据(1)中的结论,若$x+y=5,xy=\frac {9}{4}$,求$(x-y)^{2}$的值;
(3)拓展应用:若$(2025-m)^{2}+(m-2026)^{2}=7$,求$(2025-m)(m-2026)$的值.
(1)观察图②,请写出$(a+b)^{2},(a-b)^{2},ab$之间的等量关系是
$ (a + b)^{2}=(a - b)^{2}+4 a b $
;(2)根据(1)中的结论,若$x+y=5,xy=\frac {9}{4}$,求$(x-y)^{2}$的值;
(3)拓展应用:若$(2025-m)^{2}+(m-2026)^{2}=7$,求$(2025-m)(m-2026)$的值.

答案:3. (1) $ (a + b)^{2}=(a - b)^{2}+4 a b $
(2) 解: 因为 $ x + y = 5 $, $ x y=\frac{9}{4} $, 所以 $ (x - y)^{2}=(x + y)^{2}-4 x y=5^{2}-4 × \frac{9}{4}=16 $.
(3) 解: 设 $ 2025 - m = x $, $ m - 2026 = y $, 则 $ x + y = - 1 $, $ x^{2}+y^{2}=7 $, 所以 $ 2 x y=(x + y)^{2}-(x^{2}+y^{2})=1 - 7=-6 $, 所以 $ (2025 - m)(m - 2026)=x y=-3 $.
(2) 解: 因为 $ x + y = 5 $, $ x y=\frac{9}{4} $, 所以 $ (x - y)^{2}=(x + y)^{2}-4 x y=5^{2}-4 × \frac{9}{4}=16 $.
(3) 解: 设 $ 2025 - m = x $, $ m - 2026 = y $, 则 $ x + y = - 1 $, $ x^{2}+y^{2}=7 $, 所以 $ 2 x y=(x + y)^{2}-(x^{2}+y^{2})=1 - 7=-6 $, 所以 $ (2025 - m)(m - 2026)=x y=-3 $.