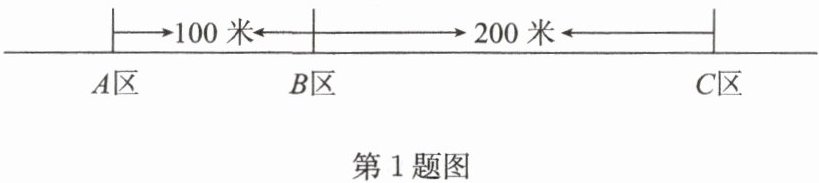
1. A,B,C 三个住宅区分别住有某公司职工 20 人,40 人,10 人,且这三个住宅区在一条大道上(A,B,C 三点共线),如图,AB=100 米,BC=200 米,为了方便职工上下班,该公司的接送车打算在此区间内设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在(
A.点 A
B.点 B
C.点 A,B 之间
D.点 B,C 之间
B
)
A.点 A
B.点 B
C.点 A,B 之间
D.点 B,C 之间
答案:1. B 点拨:①以点 A 为停靠点,则所有人的路程的和为$40×100 + 10×300 = 7000$(米);②以点 B 为停靠点,则所有人的路程的和为$20×100 + 10×200 = 4000$(米);③以点 C 为停靠点,则所有人的路程的和为$20×300 + 40×200 = 14000$(米);④当在点 A,B 之间停靠时,设停靠点到点 A 的距离是 m 米,则$0 < m < 100$,所有人的路程的和为$20m + 40(100 - m) + 10(300 - m) = 7000 - 30m > 4000$;⑤当在点 B,C 之间停靠时,设停靠点到点 B 的距离是 n 米,则$0 < n < 200$,所有人的路程的和为$20(100 + n) + 40n + 10(200 - n) = 4000 + 50n > 4000$.综上,该停靠点的位置应设在点 B 处.
2. 已知 $ a^{2}+b^{2}=3+ab $,则 $ (2a - 3b)^{2}+(a + 2b)(a - 2b) $的最大值为
22
.答案:2. 22 点拨:$(2a - 3b)^2 + (a + 2b)(a - 2b) = 4a^2 - 12ab + 9b^2 + a^2 - 4b^2 = 5a^2 + 5b^2 - 12ab$,将$a^2 + b^2 = 3 + ab$代入,得原式$= 5(3 + ab) - 12ab = 15 - 7ab$.因为$a^2 + b^2 = 3 + ab$,所以两边都加上 2ab,得$(a + b)^2 = 3 + 3ab ≥ 0$,所以$ab ≥ -1$,所以$-7ab ≤ 7$,所以$15 - 7ab ≤ 22$.
解析:
$(2a - 3b)^{2}+(a + 2b)(a - 2b)$
$=4a^{2}-12ab + 9b^{2}+a^{2}-4b^{2}$
$=5a^{2}+5b^{2}-12ab$
因为$a^{2}+b^{2}=3 + ab$,所以$5a^{2}+5b^{2}=5(3 + ab)$
原式$=5(3 + ab)-12ab=15 + 5ab-12ab=15-7ab$
由$a^{2}+b^{2}=3 + ab$,两边加$2ab$得$(a + b)^{2}=3 + 3ab≥0$
所以$3 + 3ab≥0$,即$ab≥ - 1$
则$-7ab≤7$,所以$15-7ab≤15 + 7=22$
最大值为$22$
$=4a^{2}-12ab + 9b^{2}+a^{2}-4b^{2}$
$=5a^{2}+5b^{2}-12ab$
因为$a^{2}+b^{2}=3 + ab$,所以$5a^{2}+5b^{2}=5(3 + ab)$
原式$=5(3 + ab)-12ab=15 + 5ab-12ab=15-7ab$
由$a^{2}+b^{2}=3 + ab$,两边加$2ab$得$(a + b)^{2}=3 + 3ab≥0$
所以$3 + 3ab≥0$,即$ab≥ - 1$
则$-7ab≤7$,所以$15-7ab≤15 + 7=22$
最大值为$22$
3. 若 $ a^{2}-b - 1=0 $,且 $ (a^{2}-1)(b + 2)< a^{2}b $.
(1) 求 b 的取值范围;
(2) 若 $ a^{4}-2b - 2=0 $,求 b 的值.
(1) 求 b 的取值范围;
(2) 若 $ a^{4}-2b - 2=0 $,求 b 的值.
答案:3. 解:(1)因为$a^2 - b - 1 = 0$,所以$a^2 - b = 1$,$a^2 = b + 1$.因为$(a^2 - 1)(b + 2) < a^2b$,所以$a^2b + 2a^2 - b - 2 < a^2b$,所以$2a^2 - b - 2 < 0$,所以$a^2 + a^2 - b - 2 < 0$,即$a^2 + 1 - 2 < 0$,所以$a^2 < 1$,所以$0 ≤ b + 1 < 1$,所以$-1 ≤ b < 0$.(2)因为$a^4 - 2b - 2 = 0$,所以$a^4 - 2(b + 1) = 0$.因为$a^2 = b + 1$,所以$a^4 - 2a^2 = 0$,所以$a^2 = 0$或$a^2 = 2$.又因为$a^2 < 1$,所以$a^2 = 0$,所以$b + 1 = 0$,所以$b = -1$.
解析:
(1)因为$a^{2}-b - 1=0$,所以$a^{2}=b + 1$。
因为$(a^{2}-1)(b + 2)<a^{2}b$,展开得$a^{2}b+2a^{2}-b - 2<a^{2}b$,
移项化简得$2a^{2}-b - 2<0$,将$a^{2}=b + 1$代入得$2(b + 1)-b - 2<0$,
即$2b + 2 - b - 2<0$,解得$b<0$。
又因为$a^{2}=b + 1≥0$,所以$b + 1≥0$,即$b≥-1$,
综上,$-1≤b<0$。
(2)因为$a^{4}-2b - 2=0$,且$a^{2}=b + 1$,所以$(a^{2})^{2}-2b - 2=0$,
即$(b + 1)^{2}-2b - 2=0$,展开得$b^{2}+2b + 1 - 2b - 2=0$,
化简得$b^{2}-1=0$,解得$b=1$或$b=-1$。
由(1)知$-1≤b<0$,所以$b=-1$。
因为$(a^{2}-1)(b + 2)<a^{2}b$,展开得$a^{2}b+2a^{2}-b - 2<a^{2}b$,
移项化简得$2a^{2}-b - 2<0$,将$a^{2}=b + 1$代入得$2(b + 1)-b - 2<0$,
即$2b + 2 - b - 2<0$,解得$b<0$。
又因为$a^{2}=b + 1≥0$,所以$b + 1≥0$,即$b≥-1$,
综上,$-1≤b<0$。
(2)因为$a^{4}-2b - 2=0$,且$a^{2}=b + 1$,所以$(a^{2})^{2}-2b - 2=0$,
即$(b + 1)^{2}-2b - 2=0$,展开得$b^{2}+2b + 1 - 2b - 2=0$,
化简得$b^{2}-1=0$,解得$b=1$或$b=-1$。
由(1)知$-1≤b<0$,所以$b=-1$。